Расчет момента трения в подшипниках прокатного валка

Силы трения в подшипниках прокатного валка F_тр.п (см. рис. 10.1) возникают из-за того, что на шейки валка действуют силы опорных реакций R_p1 и R_p2 на усилие прокатки Р.

Рассматривая валок как балку на двух опорах (шейках, на которые одеты подшипники, установленные наружными кольцами в отверстиях подушек), нагруженную в средней части (бочки) внешней силой (силой прокатки Р), согласно правилам расчета балок, имеем:

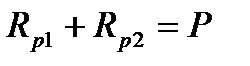, (10.13)

причем силы R_p1 и R_p2 , как и сила Р, перпендикулярны оси прокатки.

В зонах действия сил R_p1 и R_p2 внутренние кольца подшипников прижимаются к наружным, вследствие чего, при вращении в обоих подшипниках возникают силы трения, равные:

,

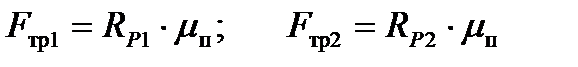где m_п – коэффициент трения в подшипниках (справочная величина, зависящая от типа подшипника) [4]:

Тип подшипника, величина m_п

Скольжения (открытого типа) 0,01-0,03

Жидкостного трения 0,003

Качения 0,003

Суммарная сила трения в двух подшипниках равна:

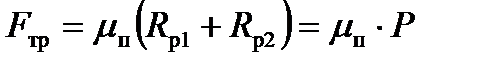(10.14)

Следовательно, момент трения в подшипниках относительно оси вращения валка равен:

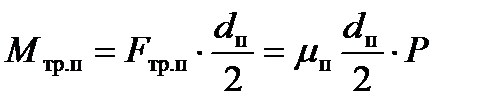, (10.15)

где d_{п –} рабочий диаметр подшипника, т.е. диаметр окружности, по которой осуществляется трение.

В подшипниках скольжения и ПЖТ d_п – это диаметр наружной поверхности шейки валка или втулки-цапфы. В подшипниках качения d_р – это диаметр условной окружности, проходящей через середину толщины тел качения (роликов), находящихся в обойме между наружным и внутренним кольцами. Величина (d_п/2) – это рабочий радиус подшипника.

Произведение 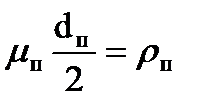(10.16)

называют радиусом круга трения в подшипниках.

Исходя их этого названия, можно дать следующее определение кругу трения в подшипниках (см. рис.10.1):

Круг трения в подшипнике прокатного валка – это умозрительная (виртуальная) окружность с центром на оси валка, имеющая радиус, равный произведению рабочего радиуса подшипника на коэффициент трения в этом подшипнике.

С учетом введенного определения, формулу (10.15) можно записать в виде:

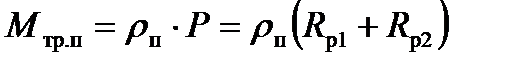. (10.17)

Выражение (10.17) можно интерпретировать следующим образом (исходя из того, что момент есть произведение силы на плечо): момент трения в подшипниках можно представить как произведение силы суммарной опорной реакции на радиус круга трения в подшипниках, причем эта сила, оставаясь вертикальной, действует по касательной к этому кругу трения.

Подставив выражение (10.8) для М_пр и выражение (10.17) для М_тр.п в уравнение (10.2), получим следующую формулу для вычисления момента М₁, приводящего во вращение прокатный валок:

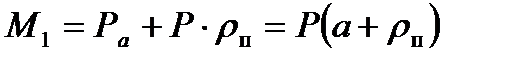(10.18)

Согласно этой формуле, момент М₁ уравновешивается моментом пары вертикальных сил: силы прокатки Р, действующей со стороны полосы в очаге деформации, и силы опорных реакций 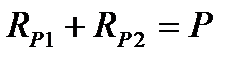, действующей в подшипниках валка по касательной к кругу трения.

Плечо момента этой пары сил равно сумме: 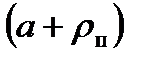(показано на рис. 10.1).

При такой интерпретации равновесия моментов, действующих на валок, опорные реакции 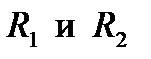следует направлять по вертикали не в осевой плоскости, проходящей через ось y, а со смещением – по касательной к кругу трения в подшипниках, как это показано на расчетной схеме рис. 10.1.