Методы расчета удельной работы прокатки

Главное преимущество метода расчета мощности прокатки, основанного на использовании удельной работы прокатки (по формуле (9.1)), перед другими методами заключается в том, что удельная работа прокатки зависит только от контактных напряжений в очаге деформации, для её вычисления не требуется никаких эмпирических коэффициентов или дополнительных экспериментальных данных.

Наиболее известная формула для расчета удельной работы прокатки – формула Финка [1;15].

; (9.9)

где 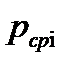- среднее значение нормального контактного напряжения (среднее удельное давление) в очаге деформации i-й клети;

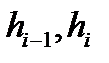- толщина полосы на входе в i-ю клеть и на выходе из неё.

Формула (9.9) основана на следующих допущениях:

1. Работу прокатки совершают только нормальные силы, вызванные нормальными контактными напряжениями p_x, а работа сил трения, вызванных касательными контактными напряжениями t_x, не учитывается.

2. Нормальные контактные напряжения направлены строго перпендикулярно оси прокатки, т.е. учитывается только работа, затрачиваемая на изменение толщины полосы.

Оба указанных допущения не соответствуют реальным условиям движения металла в очаге деформации, поскольку, в отличие от ковки и прессования, при прокатке надо не только обжимать полосу по толщине, но и, вращая валки, продвигать полосу через очаг деформации, затрачивая энергию на преодоление сил контактного трения. Кроме того, нормальные контактные напряжения p_x перпендикулярны не оси прокатки, а поверхности бочки валка, в связи с чем обжатие полосы по толщине совершают только вертикальные составляющие нормальных напряжений. Поэтому применение формулы (9.9) не гарантирует определения мощности прокатки с точностью, достаточной для инженерного расчета параметров двигателей главного привода рабочей клети.

В работах [5;2.5] опубликован новый метод расчета удельной работы и мощности прокатки, применительно к рабочим клетям широкополосных станов горячей и холодной прокатки тонких полос.

Результаты расчета по этому методу, не использующему формулу Финка (9.9), были сопоставлены с фактической мощностью двигателей главного привода ряда действующих станов. При этом было установлено, что погрешности расчета (расхождения между расчетными и фактическими значениями мощности, которые определили по измеренным электропараметрам двигателей) составили от 1% до 13% (средние значения 5-7%), что в 4-5 раз меньше погрешностей, полученным при расчете другими методами.

Новый метод расчета удельной работы прокатки базируется на двух принципиально важных положениях.

Первое положение.

Удельная работа прокатки совершается валками только с помощью касательных сил, возникающих в очаге деформации под воздействием касательных контактных напряжений, а от нормальных контактных напряжений удельная работа прокатки не зависит.

Второе положение.

Валки совершают работу прокатки только в зоне отставания очага деформации, а в зоне опережения полоса возвращает валкам часть энергии, затраченной в зоне отставания.

Для доказательства первого положения рассмотрим расчетную схему контактных напряжений, действующих на полосу в одном из участков очага деформации, например, во втором (в зоне отставания пластического участка) (рис.9.1). Чтобы упростить вычисления, соответствующий отрезок дуги контакта полосы и валка аппроксимируем хордой, угол наклона которой к оси прокатки равен a/2, где a - угол захвата (обоснование этой аппроксимации изложено в главах 6 и 8).

На рисунке показаны средние для данного участка значения контактных напряжений, действующих на полосу: нормального p₂ и касательного t₂, а также их проекции: горизонтальные (p_2г, t_2г) и вертикальные (p_2в, t_2в). Произведения этих напряжений и их проекций на площадь контакта полосы и валка в пределах данного участка (f₂) представляют собой силы, приложенные к полосе со стороны валка.

В частности, силы, вызванные средним нормальным контактным напряжением p_2, равны:

- вертикальная: ;

- горизонтальная: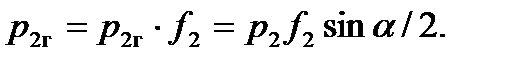

Горизонтальная сила 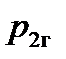совершает работу на пути (т.е. на длине второго участка), причем эта сила действует навстречу прокатываемой полосе, т.е. её работа (А_2г) отрицательная:

. (9.10)

Вертикальная сила p_2В совершает работу на пути 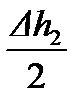, где - обжатие полосы на длине данного участка (см. рисунок).

Поскольку направление этой силы совпадает с направлением обжатия металла, работа этой силы (А_2В) положительна и равна:

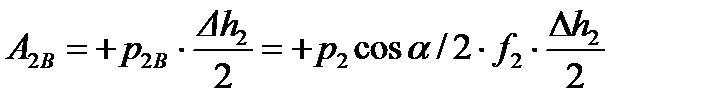(9.11)

Из схемы рис.9.1 видно, что отношение отрезков 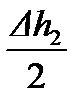и х₂ равно:

Откуда (9.12)

Подставив величину 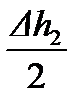, выраженную по формуле (9.12), в выражение А_2В (в формулу (9.11), получим:

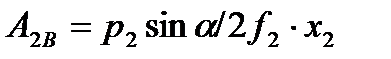. (9.13)

Рис.9.1. Расчетная схема контактных напряжений для обоснования нового

метода расчета удельной работы прокатки (на примере зоны отставания

пластического участка очага деформации).

Из сопоставления выражений (9.10) и (9.13) видно, что А_2В= -А_2г, т.е. сумма работ вертикальной и горизонтальной сил равна нулю. Таким образом, работа сил, вызванных нормальным контактным напряжением, не расходуется на прокатку полосы, так как полезная работа вертикальной силы полностью затрачивается на погашение отрицательной работы горизонтальной силы. Аналогичные результаты получаются для всех остальных участков очага деформации (студентам рекомендуется проверить это самостоятельно).

В отличие от нормального напряжения, в зоне отставания работы, совершаемые вертикальной и горизонтальной силами, вызванными касательными напряжениями, являются положительными, т.к. направления их действия совпадают с направлениями движения и деформации полосы (это видно из схемы на рис.9.1).

Таким образом, первое из двух положений, на которых базируется новый метод расчета удельной работы прокатки, доказано.

Для доказательства второго положения необходимо обратить внимание на тот факт, что в зоне опережения очага деформации средняя скорость полосы в любом поперечном сечении 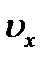больше окружной скорости бочки валка . Это значит, что в данной зоне касательные силы, приложенные к полосе со стороны валка, направлены назад (навстречу движению полосы), т.е. валки не совершают полезной работы, а притормаживают полосу, препятствуя её движению. Полосе приходится затрачивать в зоне опережения часть кинетической энергии, полученной от валков в зоне отставания, чтобы преодолевать сопротивление её движению, создаваемое валками.

Ниже изложен метод расчета удельной работы прокатки, основанный на двух сформулированных выше положениях.

Изложение выполнено на примере расчета удельной работы прокатки тонкой полосы в i-й рабочей клети широкополосного стана, в соответствии с расчетной схемой рис. 9.2, для очага деформации, имеющего одно нейтральное сечение толщиной .

Составляющие работы прокатки a_j вычисляют сначала отдельно на каждом участке очага деформации (j- номер участка: j=1- первого упругого, j =2 - зоны отставания пластического участка, j=3 – зоны опережения пластического участка, j=4 – второго упругого, где происходит частичное восстановление толщины полосы).

Рис. 9.2 Расчетная схема для определения удельной работы прокатки.

Работа прокатки в очаге деформации i-й клети будет равна: сумме величин a_j:

. (9.14)

Если очаг деформации не имеет нейтральных сечений, то он содержит по длине 3 участка, находящихся в зоне отставания: j=1 - первый упругий, j=2 – пластический, j=3 – второй упругий.

Удельная работа прокатки в i-й клети с таким очагом деформации равна:

. (9.15)

Если очаг деформации имеет 2 нейтральных сечения, то он содержит по длине 5 участков (j=1…5): первые три такие же, как в очаге с одним нейтральным сечением, а второй упругий участок разделяется на два: первый по ходу движения полосы (j=4) находится в зоне опережения, а второй (j=5) представляет собой дополнительную зону отставания.

Удельная работа прокатки в i-й клети с очагом деформации, имеющем два нейтральных сечения, равна:

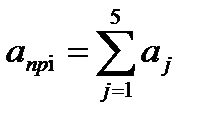. (9.16)

Величины a_j (удельные работы прокатки на каждом j-м участке очага деформации) рассчитывают следующим образом.

1. Определяют среднее значение касательных напряжений, действующих на j-м участке очага деформации:

(9.17)

где h_j-1, h_j - значения толщины полосы h_x в начале и в конце j-го участка;

t_x – переменное значение касательного напряжения в функции толщины полосы:t_x=t_x(h_x).

Для использования выражения (9.17) в практических расчетах необходимо знать зависимости t_x от переменной толщины полосы h_x на каждом участке очага деформации. Эти зависимости приведены в п.п. 6.4 и 6.5 главы 6.

а) Средние значения t_x на упругих участках очага деформации

Согласно объяснениям, приведенным в главах 5,6, на упругих участках очагов деформации, как при горячей, так и при холодной прокатке принимают допущение о действии закона трения скольжения:

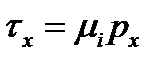(9.18)

где m_i – среднее для i-й клети значение коэффициента трения в очаге деформации; p_x- переменное нормальное контактное напряжение.

Поэтому средние значения касательных напряжений на этих участках можно вычислить, не прибегая к интегрированию:

, (9.19)

где p_j – среднее значение нормального контактного напряжения p_x на j-м упругом участке этой клети.

Эмпирические формулы для определения коэффициента трения приведены в главе 6. В клетях стана холодной прокатки величину m_j рекомендуется рассчитывать по формуле (6.20) (см. п. 6.3,в).

В клетях стана горячей прокатки величину m_j рекомендуется рассчитывать по формуле (6.64) (см. п. 6.4,в).

Формулы для расчета средних значений нормальных контактных напряжений p_j на упругих и на пластических участках очага деформации приведены в главе 8, в таблице 8.1.

б) Средние значения t_x на пластических участках очага деформации стана холодной прокатки

В главе 5 (п.5.3) и в главе 6 (п.6.3) показано, что связь между нормальными и касательными напряжениями, выражаемая формулой (9.18) (трение скольжения), справедлива не только для упругих, но и для пластических участков очага деформации при холодной прокатке. Поэтому на этих участках величину можно рассчитывать по формуле (9.19), а выражения p_j, входящие в эту формулу, приведены, как и для упругих участков, в таблице 8.1 главы 8.

в) Средние значения t_x на пластических участках очага деформации стана горячей прокатки

В главе 6, п.6.5, на рис. 6.16 показан график изменения касательных напряжений t_x по длине очага деформации при горячей прокатке. На этом графике в пластической области напряжения t_x изменяются согласно формуле (6.61):

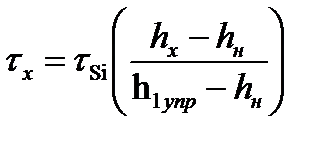(6.61)

где h_н – толщина полосы в нейтральном сечении;

h_x – переменная толщина полосы;

h_1упр = h_i-1 - Dh_1упр – толщина полосы на границе первого упругого и пластического участков;

h_i-1 – толщина полосы на входе в i-ю клеть;

t_Si – сопротивление чистому сдвигу материала полосы в i-й клети, зависящее от материала полосы и её температуры, скорости деформации, относительного обжатия (t_Si »0,57s_ф.пл.i).

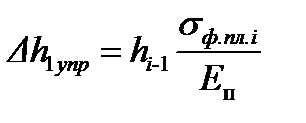- максимальная упругая деформация полосы в конце первого упругого участка;

s_ф.пл.i – среднее значение сопротивления пластической деформации полосы в i-й клети.

Из формулы (6.61) и графика рис. 6.16 видно, что зависимость t_x(h_x) общая для зон отставания и опережения. На участке (h_1упр ¸ h_н) формула (6.61) дает зависимость t_x(h_x) в зоне отставания, а на участке (h_н ¸ h_2упр) - зависимость t_x(h_x) в зоне опережения (h_2упр- граница этой зоны и второго упругого участка).

Учитывая противоположное направление касательных напряжений в зонах отставания и опережения их средние значения следует определять отдельно, путем интегрирования выражения (6.61) в соответствующих диапазонах изменения h_x:

- в зоне отставания (j=2):

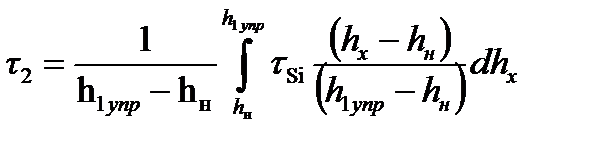; (9.20)

- в зоне опережения (j=3):

(9.21)

Окончательные выражения t₂ и t₃ имеют вид:

(9.22)

Изучающим теорию прокатки рекомендуется выполнить самостоятельно интегрирование выражений (9.20) и (9.21), убедившись в правильности формул (9.22).

2. После определения среднего значения касательных напряжений в j-м участке очага деформации переходят непосредственно к расчету удельной работы прокатки на этом участке.

Для этого, в соответствии с расчетной схемой (рис.9.2), вычисляют работу касательных сил на этом участке – отдельно в горизонтальном (вдоль оси прокатки) и вертикальном (перпендикулярно оси прокатки) направлениях, затем эти работы суммируют и относят к единице объема полосы.

Последовательность этих действий удобнее показать на конкретном примере. Ниже приведен вывод формулы удельной работы прокатки для зоны опережения пластического участка очага деформации с одним нейтральным сечением (j=3, рис. 9.3).

Рис. 9.3. Расчетная схема для определения удельной работы прокатки в зоне опережения пластического участка очага деформации (j=3).

На расстоянии х от начала координат выделим элемент протяженностью dx по оси x. При прокатке толщина полосы в пределах этого элемента изменяется от до h_x, т.е. обжатие составляет dh_x.

Определим по отдельности работу горизонтального и вертикального смещения материала полосы, имеющей длину на выходе из валков L₁ и конечную толщину h₁. Согласно закону постоянства объема, при отсутствии уширения имеем:

, (9.23)

где L_x – длина, которую имеет полоса при прохождении через сечение с координатой x.

Работа вертикального смещения полосы в пределах выделенного элемента dAв совершается каждым валком на пути dh_x/2, при этом силы вертикального смещения, вызванные касательными напряжениями, представляют собой произведения вертикальных проекций напряжений t_3В, на соответствующую площадь. Площадь действия для этих напряжений , где b –ширина полосы, так как через выделенный элемент проходит при прокатке вся полоса длиной L_x, а поверхность контакта ей с валком отклонена от оси прокатки на угол a/2.

При определении работы прокатки необходимо учесть, что вертикальная составляющая касательного напряжения t_3В действует в направлении, противоположном обжатию полосы, т.е. препятствует этому обжатию, поэтому работа вертикального смещения со стороны одного валка при прохождении всей полосы через выделенный элемент будет отрицательной и составит:

(9.24)

Из рис. 9.3 видно, что

(9.25)

Подставив (9.23) и (9.25) в (9.24), получим выражение для работы вертикального смещения, совершаемой в пределах выделенного элемента двумя валками:

, (9.26)

где V – объем прокатанной полосы.

Следовательно, удельная работа вертикального смещения полосы в пределах зоны опережения (j=3) будет равна:

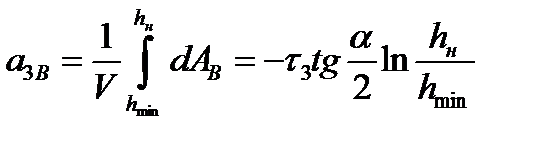(9.27)

Удельную работу горизонтального смещения полосы в зоне опережения определяют с помощью аналогичных преобразований, а затем суммируют с удельной работой вертикального смещения. Аналогичными преобразованиями определяют удельные работы прокатки на остальных участках очага деформации.

Изучающим теорию прокатки рекомендуется эти преобразования выполнить самостоятельно.

Полученные таким образом выражения удельных работ прокатки, совершаемых валками на каждом из участков очага деформации, приведены в табл. 9.1.

Таблица 9.1

Расчетные формулы удельных работ прокатки

на каждом участке очага деформации (для очагов всех трех типов)

Номер участка j	Название участка	Кол-во нейтральных сечений в очаге деформации	Расчетная формула aj, МДж/м3
	Участок упругого сжатия полосы на входе в очаг деформации	0; 1; 2
	Зона отставания пластического участка	1; 2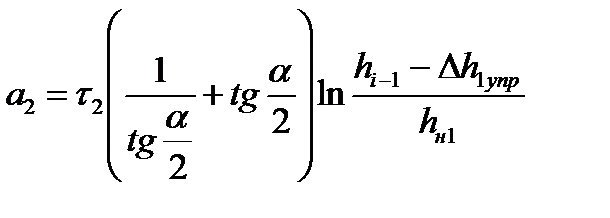
2-3	Пластический участок, состоящий только из зоны отставания (зона опережения отсутствует)
	Зона опережения пластического участка	1; 2
	Второй упругий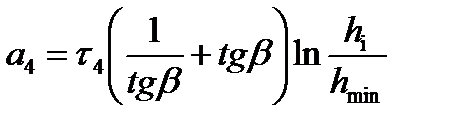
	участок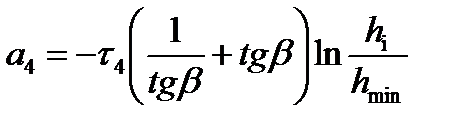
	Зона опережения второго упругого участка
	Зона отставания второго упругого участка