Расчет момента прокатки

Как видно из уравнения (10.1), на каждый валок действует половина момента прокатки - произведение силы прокатки на её плечо (кратчайшее расстояние от оси вращения валка до линии действия этой силы). Чтобы найти плечо силы прокатки, надо знать её направление.

При простом процессе прокатки направление силы прокатки Р можно определить из уравнения равновесия полосы в очаге деформации (см. рис. 10.1):

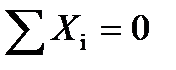, (10.6)

где Х_i – проекции всех сил, действующих на полосу.

При простом процессе прокатки на полосу действуют силы только со стороны валков в очаге деформации, другие внешние силы (натяжений, подпора) отсутствуют.

Если предположить, что сила R, действующая со стороны каждого валка на полосу (равнодействующая сил прокатки и трения), отклонена от вертикали на угол j, то уравнение (10.6) примет вид:

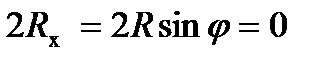_, (10.7)

где R_x – проекция на ось х силы R.

Поскольку сила R заведомо не равна нулю, из выражения (10.7) следует, что sinj =0, что возможно только в случае, когда угол j=0.

Отсюда следует, что при простом процессе прокатки равнодействующая всех сил, действующих в контакте полосы и валка, направлена вертикально. Но эта равнодействующая и является силой прокатки Р (см. главу 8). Таким образом, можно сделать окончательный вывод: если на полосу не действуют другие силы, кроме сил со стороны валков в очаге деформации, то сила, действующая между каждым валком и полосой, направлена перпендикулярно оси прокатки и равна силе прокатки.

Необходимо сделать одну оговорку: этот вывод можно распространить на следующий частный случай отступления от простого процесса прокатки: если к полосе приложены силы переднего и заднего натяжения, равные по величине, то в уравнении равновесия полосы (10.6) эти силы сократятся, т.е. уравнение (10.7) останется в силе и угол j по-прежнему будет равен нулю.

Поэтому силы прокатки останутся вертикальными (перпендикулярными оси х), если на полосу действуют вдоль оси х силы переднего и заднего натяжения, равные по величине.

Установив направление сил Р, можно определить момент прокатки по формуле (см. рис.10.1):

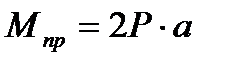, (10.8)

где а – плечо силы прокатки относительно оси вращения валка (кратчайшее расстояние от этой оси до линии действия силы).

В формуле (10.8) учитываются силы Р, которые действуют со стороны полосы на каждый валок. Они, согласно 3-ему закону Ньютона, равны по величине силам, действующим со стороны каждого валка на полосу, но противоположно направлены.

Чтобы использовать формулу (10.8) в практических расчетах, надо знать величину а, определяющую координату точки х по оси прокатки, в которой действует сила Р (т.е. точку приложения на дуге контакта полосы и валка равнодействующей всех сил, вызванных контактными напряжениями).

В большинстве известных методик, разработанных в 20 веке, для расчета величины а рекомендуется следующая эмпирическая формула:

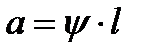, (10.9)

где l – длина очага деформации, y - эмпирический коэффициент, называемый коэффициентом плеча силы прокатки.

В литературе приводятся многочисленные эмпирические выражения или числовые значения этого коэффициента, согласно которым, он может изменяться в широком диапазоне: y = 0,35…0,5. Поэтому использование формулы (10.9) вносит существенную погрешность в расчет момента и мощности главного привода рабочей клети, достигающую 30-40% и более от фактических значений.

В современных условиях, когда задачи повышения энергоэффективности и экономии энергии в металлургическом производстве приобрели большую актуальность, требуется более точный метод расчета плеча силы прокатки, не использующий эмпирический коэффициент y.

Такой метод разработан и опубликован в работах [5;25].

Сущность его в том, что сначала определяют мощность прокатки в i-й клети N_прi по методике, изложенной в главе 9 данного учебника, а затем используют связь между моментом и мощностью прокатки:

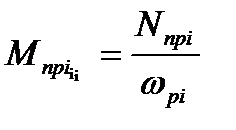, (10.10)

М_прi – момент прокатки в i-й клети, 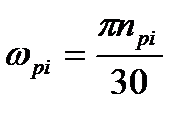- угловая скорость прокатных (рабочих) валков i-й клети, n_pi –число оборотов этих валков в минуту.

Подставив в (10.10) выражение М_прi по формуле (10.8), получают искомую величину плеча силы прокатки:

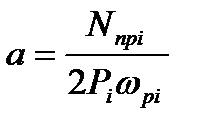, (10.11)

Формула (10.11) не содержит эмпирических коэффициентов, а входящие в нее величины N_прi и P_i , вычисляемые по методикам, изложенным в главах 8 и 9, имеют наименьшие погрешности, по сравнению с другими известными методиками.

При их расчете не используются никакие эмпирические величины, кроме общепринятых: коэффициента трения в очаге деформации и сопротивления деформации прокатываемого металла.

Вычислив величину а по формуле (10.11), легко найти угол b, определяющий точку приложения силы прокатки на дуге захвата (см. рис. 10.1):

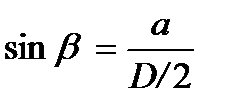, (10.12)

где D – диаметр бочки прокатного валка.