Методы расчета площади контакта металла с валками

Контакт полосы с каждым из валков происходит по некоторой криволинейной поверхности, площадь которой зависит от кривизны цилиндрической поверхности бочки, искаженной упругим сплющиванием, длины очага деформации, а также от формы калибра (если прокатывают сортовой или фасонный профиль).

Точно определить площадь контакта в функции всех этих факторов очень сложно, поэтому величину F_контi, входящую в формулу силы прокатки (8.2), рассчитывают, используя некоторые упрощающие допущения, исходя из той цели, чтобы погрешность расчета силы прокатки (разность между рассчитанной и измеренной величинами F_i) была по возможности минимальной.

Одно из допущений состоит в том, что в качестве величины F_контi принимают площадь не фактической поверхности контакта полосы и валка, а ее горизонтальной проекции на плоскость, проходящую через ось прокатки.

На основе этого допущения при прокатке полосы прямоугольного поперечного сечения величину F_контi определяют по формуле:

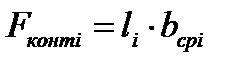, (8.17)

где l_i – длина очага деформации в i-й рабочей клети;

b_срi – средняя ширина полосы в очаге деформации.

Если прокатка происходит с уширением, то кривая, по которой в очаге деформации движется боковая кромка полосы, близка по форме к экспоненте, поэтому среднюю ширину полосы вычисляют по формуле:

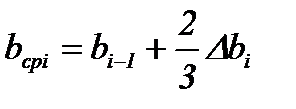, (8.18)

где b_i-1 – ширина полосы на входе в i-ю клеть;

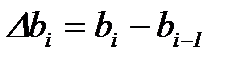- абсолютное уширение;

b_i – ширина полосы на выходе из i-й клети.

При двумерной информации, когда уширение практически отсутствует (прокатка тонких широких полос):

,

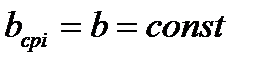где b – постоянная во всех клетях ширина полосы.

Длину очага деформации l_i для расчета F_контi по формуле (8.17) определяют следующим образом:

а) при горячей прокатке полос толщиной h_i ≥ 8…10 мм, когда упругое сплющивание валков и полосы незначительно и им можно пренебречь, используют приближенную формулу, вывод которой дан в главе 3:

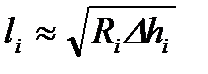, (8.19)

где R_i - радиус бочки валка в i-й клети;

Δh_i – абсолютное обжатие полосы в очаге деформации i-й клети.

б) при горячей и холодной прокатке полос толщиной h_i < 8 мм пренебрегать совместным упругим сплющиванием валков и полосы в очаге деформации не следует, т.к. это значительно увеличивает погрешность расчета площади контакта, а значит и силы прокатки. Доля длины упругих участков от общей длины очага деформации может достигать:

- при горячей прокатке полос толщиной h_i ≤ 1,5 мм – 17 - 21%;

- при холодной прокатке полос толщиной h_i ≤ 0,5 мм – 60% и более (чем тоньше полоса, тем больше эта доля).

Поэтому для полос указанного сортамента длину очага деформации рассчитывают с учетом упругого сплющивания полосы и валков. В отличие от длины l_i, определяемой формулой (8.19), ее обозначают l_сi, добавляя индекс ''с'', свидетельствующий об учете упругого сплющивания. Формулы для расчета общей длины очага деформации l_сi и длин ее составных частей (упругих и пластических участков) приведены в главе 6, при изложении методики расчета переменных контактных напряжений. Однако, подробного вывода этих формул дано не было, он излагается в данной главе, поскольку этот вывод имеет существенное значение для понимания методики расчета силы прокатки. Впервые этот вывод изложен в работах А.И. Целикова и его учеников [1;15]. Расчетная схема, на основе которой сделан вывод формулы l_сi, представлена на рис. 8.3,а.

б)

а)

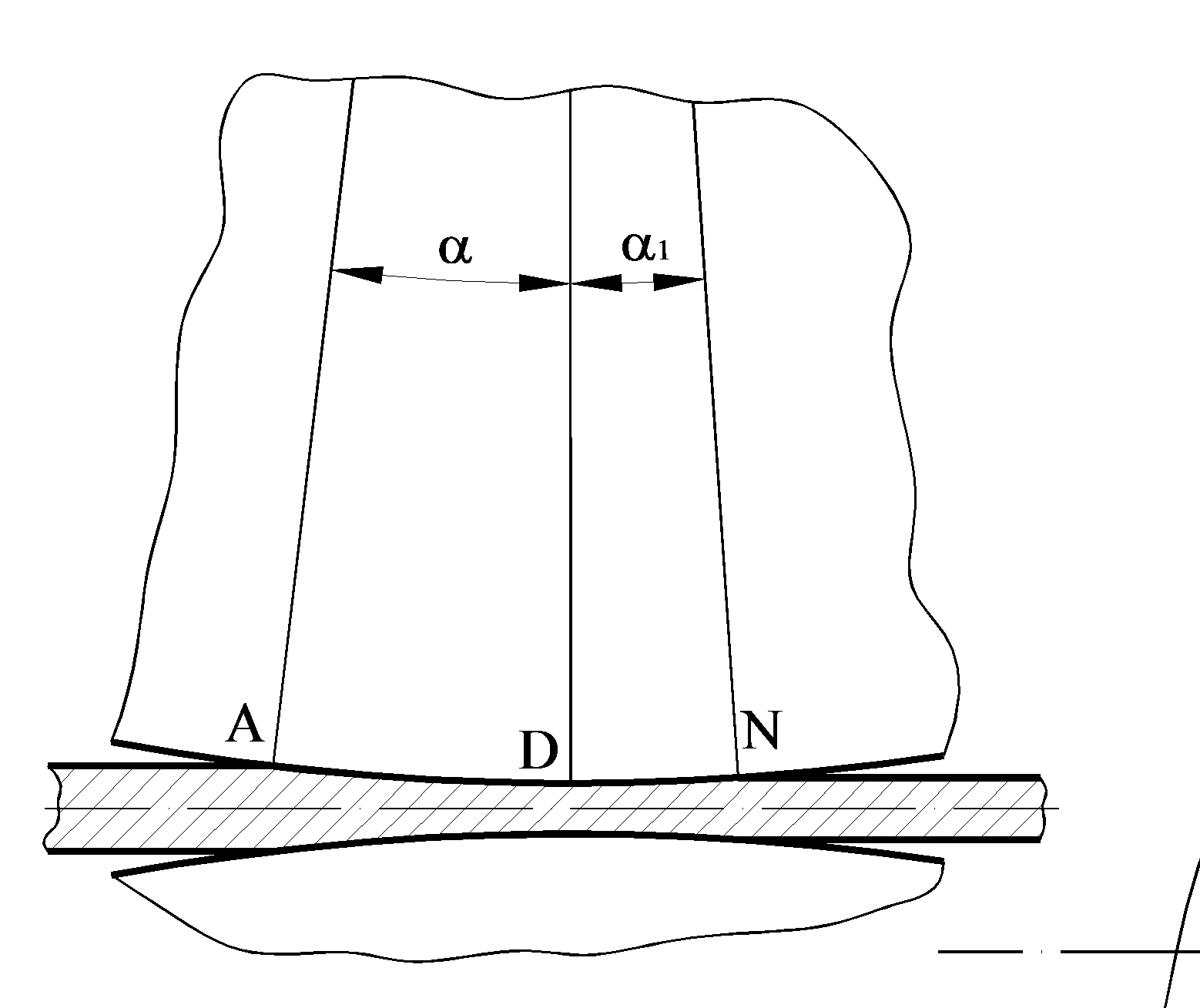
Рис. 8.3 Расчетная схема для вывода формулы длины очага деформации с учетом упругого сплющивания валков и полосы (а) и форма дуги контакта при реальных углах захвата в процессе прокатки тонких полос (б)

На схеме показаны:

h_i-1 – толщина полосы на входе в валки;

AB – дуга захвата, если не учитывать упругое сплющивание валка;

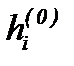- толщина, которую имела бы полоса на выходе из очага деформации, если бы ее контакт с валками происходил только по дуге АВ;

ADC – дуга захвата, если учитывать радиальное упругое сплющивание валка

W_в, но не учитывать упругую деформацию полосы, происходящую на выходе ее из очага деформации.

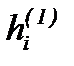- толщина, которую имела бы полоса на выходе из очага деформации, если учитывать только упругое сплющивание валков.

Необходимо иметь в виду, что в начале очага деформации, правее точки А, полоса не сразу подвергается пластической деформации, а сначала сжимается упруго. И лишь только после того, как сопротивление упругому сжатию достигнет предельного для материала значения (на входе в i-ю клеть оно равно σ_фi-1), начинается процесс пластической деформации полосы.

Он заканчивается после прохождения полосой точки D, лежащей на вертикальной осевой плоскости валка EOB.

Правее точки D поверхность бочки начинает удаляться от оси прокатки и межвалковый зазор увеличивается. Однако, толщина полосы не остается после этого постоянной, равной 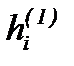, т.к. металл имеет свойство после пластической деформации упруго восстанавливать часть первоначальной толщины. Таким образом, на участке очага деформации длиной x₁ имеет место упруго-пластическая деформация обжатия полосы, а на участке длиной x_2упр – только упругая деформация, состоящая в возврате части толщины полосы, равной 2W_П (см. схему «а» рисунка 8.3, где W_П – упругое увеличение толщины полосы со стороны одного валка).

В результате общая длина очага деформации будет равна:

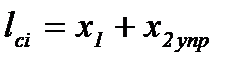, (8.20)

где x₁ соответствует отрезку дуги AD, а x₂ соответствует отрезку дуги DN, причем точка N возникает в том месте, где полностью заканчивается упругое восстановление части толщины полосы. Точка N определяет длину отрезка x_2упр, окончательную толщину полосы на выходе из i-й клети h_i и ее абсолютное обжатие:

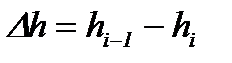, (8.21)

Таким образом, чтобы получить расчетную формулу l_сi, необходимо определить длины x₁ и x_2упр.

А.И. Целиков решил эту задачу, начиная с определения длины x_2упр, соответствующей отрезку DN дуги захвата [1]. Поскольку на участке DN в контакте валка и полосы имеют место только упругие деформации, он предложил использовать для расчета x₂ классическую формулу теории упругости – формулу Герца (случай упругого контакта цилиндра и плоскости):

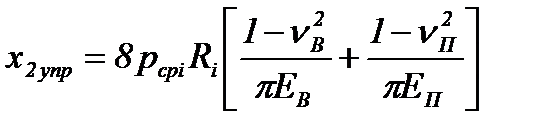, (8.22)

где p_срi – среднее удельное давление;

R_i – радиус бочки валка;

ν_B, ν_П – коэффициенты Пуассона материалов валков и полосы;

Е_В, Е_П – модули упругости материала валков и полосы.

Величину x₁ можно найти из соотношения сторон двух пар подобных прямоугольных треугольников: ABE и ABF, BNE и BNG (рис. 8.3,а):

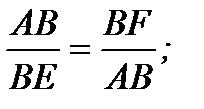
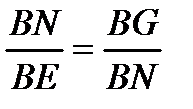. (8.23)

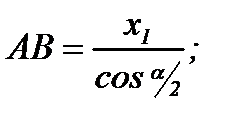
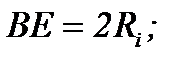
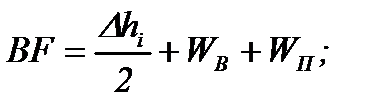
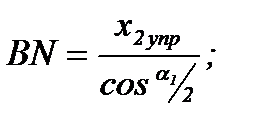
Подставив в равенства (8.23) значения отрезков: 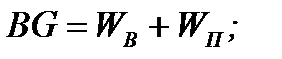после простых алгебраических преобразований получим:

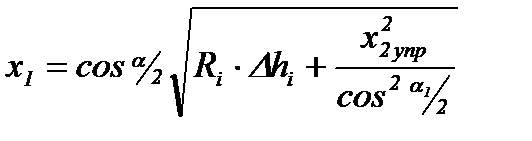, (8.24)

(изучающим теорию прокатки рекомендуем преобразования равенств (8.23) к виду (8.24) выполнить самостоятельно).

Заметим, что на схеме рис. 8.3,а углы α (угол захвата) и α₁ изображены значительно бóльшими, чем в реальности. Это сделано для того, чтобы четко показать все отрезки (W_В, W_П, 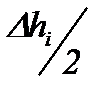) и объяснить вывод формулы (8.24).

Фактически при прокатке тонких полос углы захвата не превышают 10° (α_max=10°), а угол α₁, образующийся на участке упругого восстановления части толщины полосы, не превышает 6° (α_max=6°). В связи с этим форма дуги AND, образующей очаг деформации, имеет при реальных углах α и α₁ вид, показанный на схеме рис. 8.3,б. Как видно, отрезки этой дуги AD и DN очень близки по форме к отрезкам прямых, поэтому их линейная аппроксимация в энергосиловых расчетах вполне обоснована.

Кроме того, 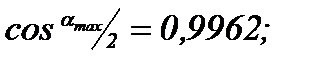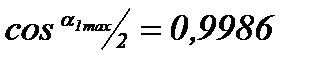, поэтому с погрешностью, не превышающей 0,5%, можно принять в формуле (8.24) 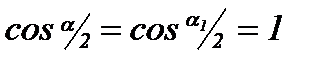, и окончательно эта формула будет иметь вид [8.1]:

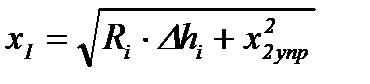. (8.25)

Таким образом, алгоритм вычисления длины очага деформации с учетом упругого сплющивания валков и полосы заключается в следующем:

1. Рассчитывают длину x_2упр по формуле (8.22).

2. Рассчитывают длину x₁ по формуле (8.25).

3. Рассчитывают длину l_сi по формуле (8.20).

Уточненный расчет длины второго упругого участка x_2упр при холодной прокатке.

Опыт энергосиловых расчетов широкополосных станов показал, что изложенная методика определения длины очага деформации с учетом упругого сплющивания валков и полосы позволяет рассчитать силу прокатки с погрешностью, не превышающей 5-10%, при горячей прокатке, т.к. длина второго упругого участка очага деформации в этом случае не превышает 15-21% общей длины очага деформации. И если длина x_2упр по формуле Герца (8.22) рассчитана неточно, например, с погрешностью 30%, то общая погрешность вычисления длины l_сi не превысит 30%·0,17=5,1%.

На станах холодной прокатки, особенно при производстве наиболее тонких полос (толщиной менее 0,5 мм), длина упругих участков достигает 50% и более, поэтому требования к точности вычисления x_2упр на этих станах более жесткие.

Анализ этого вопроса, изложенный в главе 6, показал, что формула Герца (8.22) для расчета длины x_2упр не учитывает некоторых существенных особенностей контакта валков и полосы на втором упругом участке очага деформации. В теории упругости эта формула получена для случая прижатия неподвижного цилиндра к упругому полупространству, ограниченному плоской поверхностью.

При прокатке валки вращаются, а полоса, в отличие от полупространства, движется, имеет конечную толщину и переменную жесткость, возрастающую по мере обжатия, причем между ней и валками действуют напряжения трения. Следовательно, формула (8.22) не учитывает факторы, которые могут влиять на длину упругого участка x₂: трение между полосой и валками, изменение ее толщины и жесткости по мере обжатия.

Для учета этих факторов в главе 6 приведена уточненная формула (6.40), которая отличается от формулы Герца (8.22) введением в нее поправочного коэффициента К_попрi. Для удобства изучения студентами материала главы 8 ниже повторно приведены из главы 6 уточненная формула (6.40) для расчета x_2упр и формула (6.41) для расчета поправочного коэффициента К_попрi (этим формулам присвоены новые номера, соответствующие порядку нумерации формул главы 8).

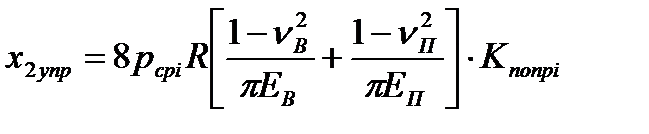. (8.26)

Величина К_попрi зависит от значения комплекса:

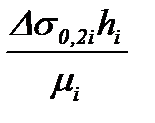, (8.27)

где 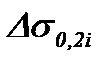- приращение условного предела текучести полосы от исходного значения (наклеп полосы на выходе из i-ой клети):

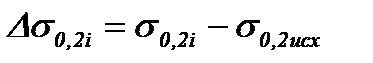; (8.28)

h_i, μ_i – толщина полосы на выходе из i-й клети и среднее значение коэффициента трения в ее очаге деформации.

Если 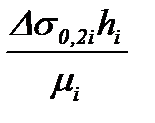> 5200 МПа·мм, то К_попрi=1.

Если 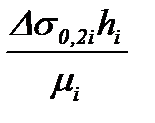≤ 5200 МПа·мм, то К_попрi вычисляют по регрессионному уравнению:

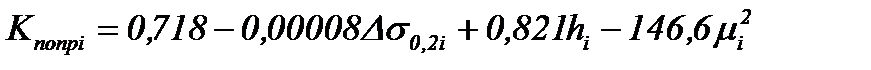; (8.29)

(размерности : 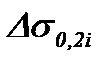: МПа, h_i: мм).

Регрессионное уравнение (8.29) получено в результате статистической обработки более 7000 режимов прокатки, их технологических и энергосиловых параметров, содержащихся в базах данных АСУТП действующих станов. Обработанные режимы охватывают широкий спектр параметров: толщины h_i = 0,27…1 мм, коэффициенты трения μ_i = 0,034…0,072; приращение предела текучести: 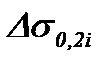= 336…519 МПа. Множественный коэффициент детерминации для уравнения (8.29) оказался равным: R² = 0,974, что свидетельствует о статистической достоверности этого уравнения.

Из выражений (8.27) и (8.29) видно, что из факторов, не учитываемых формулой Герца (8.22), на длину упругого участка деформации наибольшее влияние оказывают толщина полосы и коэффициент трения: чем тоньше полоса и чем больше коэффициент трения, тем меньше длина x_2упр, по сравнению со значением, полученным по формуле (8.22).

Так, например, в 5^й клети 5^тиклетевого стана «1700», при прокатке полосы из стали 08пс толщиной h₅=0,3 мм с коэффициентом трения μ₅=0,036 К_попр5=0,8. Увеличение коэффициента трения до значения μ₅=0,049 вызывает снижение поправочного коэффициента до величины К_попр5=0,6. Таким образом, для указанных условий холодной прокатки наиболее тонких полос в 5^й клети формула Герца дает существенно завышенное значение x_2упр (а, следовательно и всей длины очага деформации): при μ₅=0,036 это завышение составляет 20%, а при μ₅=0,049 оно возрастает до 40%.

Расчет площади контакта металла с валками при прокатке в калибрах [15].

Поверхность контакта при прокатке в калибрах имеет сложную форму, зависящую от профиля сортового или фасонного металла. Точно вычислить ее площадь аналитическим методом крайне сложно, поэтому данную задачу решают приближенными инженерными методами: графическим (с помощью приемов начертательной геометрии), графоаналитическим или аналитическим. Сущность этих методов изложена в книге [15].

В современных условиях, когда инженерные расчеты технологии и оборудования прокатного производства выполняют с использованием компьютерных средств, применение графических методов нецелесообразно. Лучше воспользоваться проверенными на практике эмпирическими или полуэмпирическими формулами.

К их числу относятся формулы В.Г. Дрозда для расчета контактной площади при прокатке сортовых профилей, исходя из наиболее распространенных схем калибровки квадрата, овала и ромба. Эти формулы приведены в таблице 8.5. Для расчета площади контакта при прокатке профилей сложной формы (уголков, балок, швеллеров и т.д.) можно, используя метод приведенной полосы, рассчитать по формуле (8.14) обжатие Δh_i, по формуле (8.16) катающий радиус R_кi, по формуле (8.15) длину очага деформации l_i, а затем определить среднее значение ширины профиля в очаге деформации В_срi, и, наконец, вычислить площадь контакта: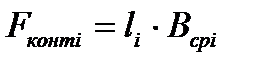

Таблица 8.5

Контактные площади при прокатке сортовых профилей

(формулы В.Г. Дрозда)

№	Схема калибровки	Формула контактной площади	Примечания
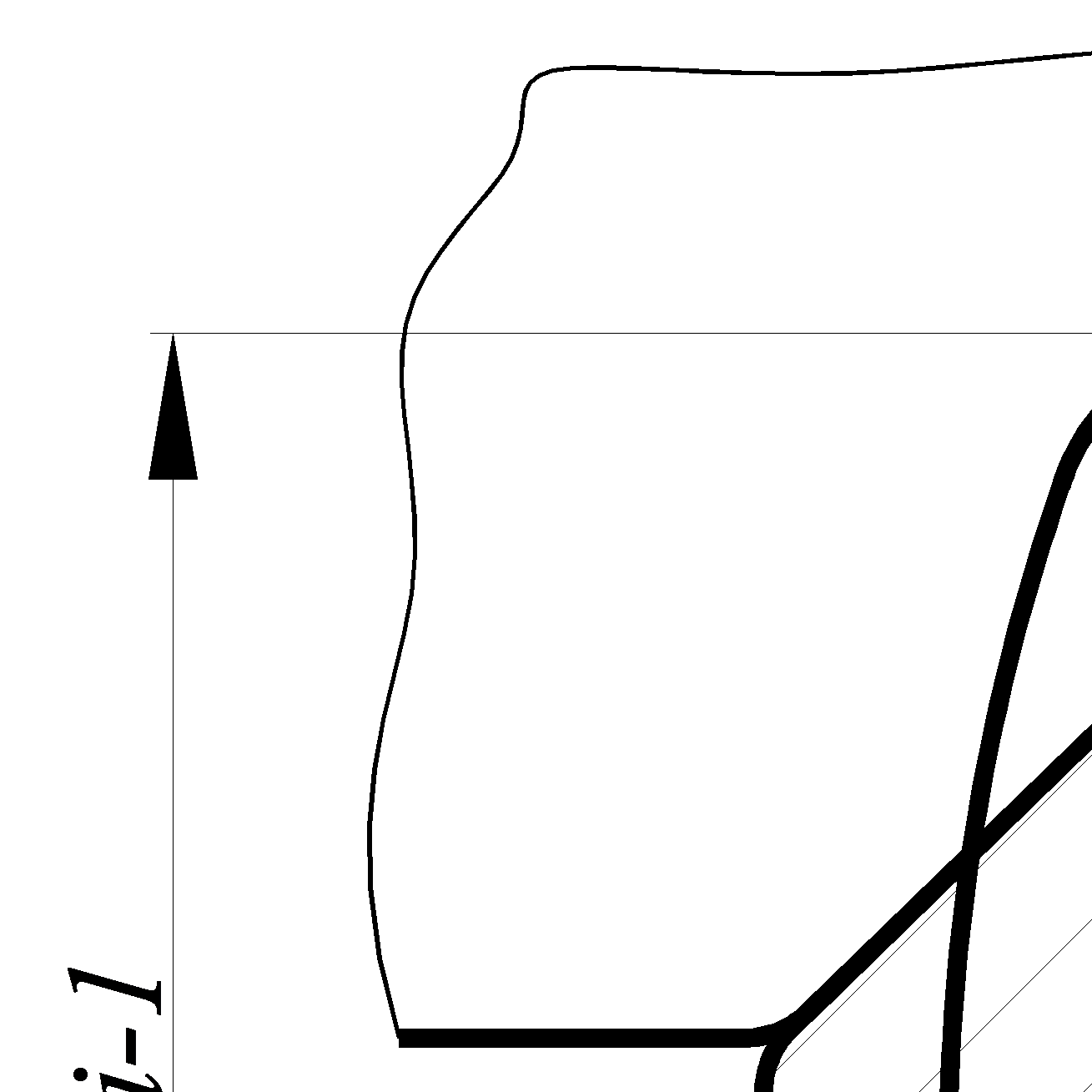
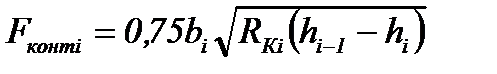
	Прокатка квадрата из овала		RКi – радиус валка в середине калибра. Остальные размеры – на схемах.
	Прокатка овала из квадрата
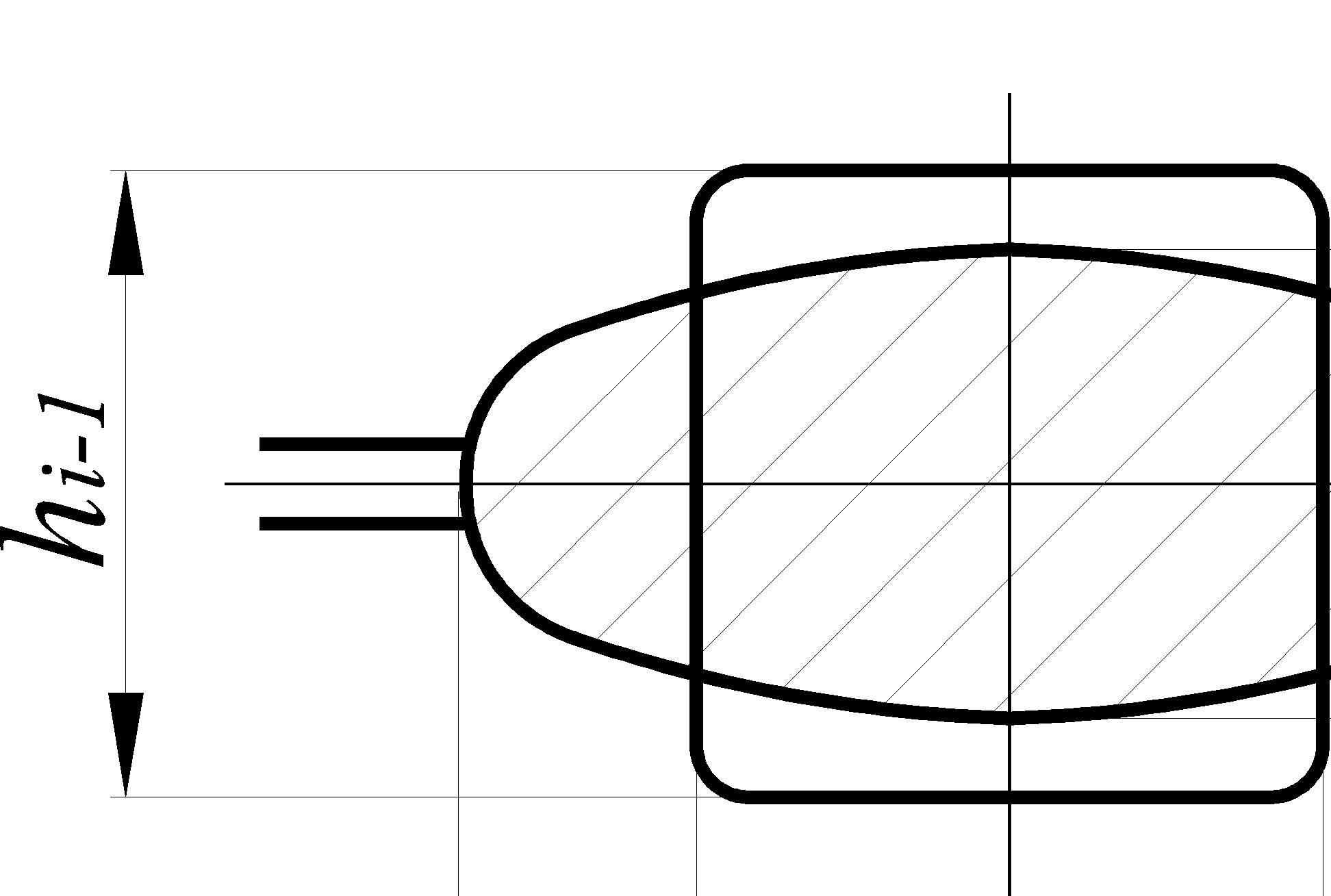
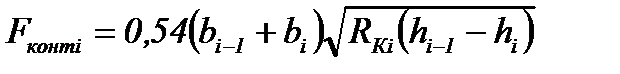
	Прокатка ромба или квадрата из ромба

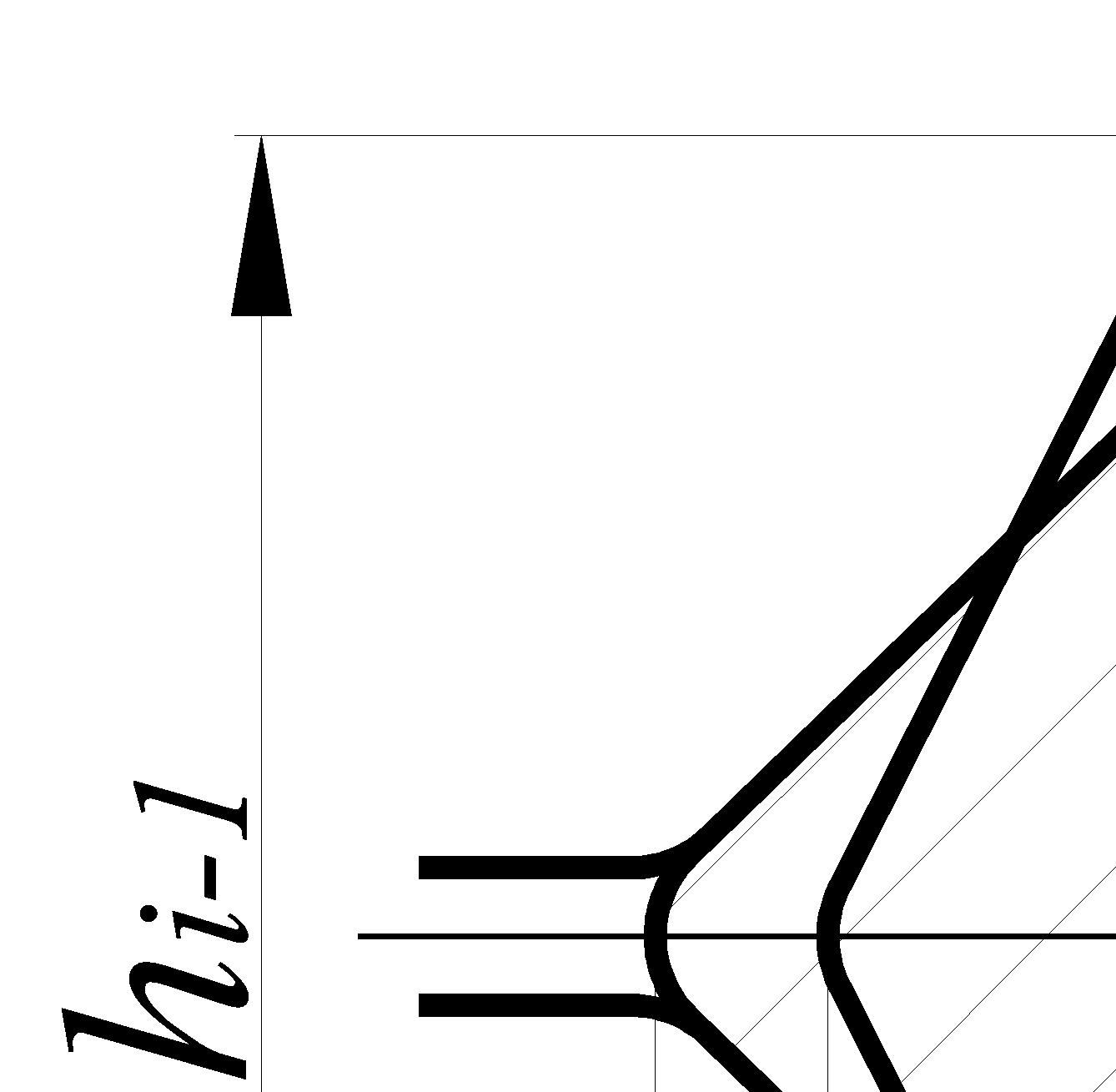
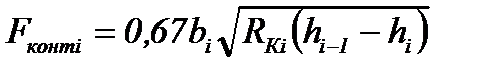
О других методах расчета величины F_контi при прокатке в калибрах можно прочитать в книгах [11.5; 11.10].