Методы расчета силы прокатки

Общие положения.

Силой прокатки называют силу, возникающую в очаге деформации между полосой и каждым из валков под воздействием контактных напряжений. Чаще всего ее обозначают латинской буквой P. На стане, содержащем несколько рабочих клетей, этой силе присваивают индекс “i” – номер рабочей клети: P_i.

Обычно при расчете силы прокатки учитывают действие только нормальных контактных напряжений p_x, а касательными контактными напряжениями τ_x в этом расчете пренебрегают.

Вычисление силы прокатки – необходимый элемент конструкторского и технологического расчетов прокатного стана.

По силе прокатки проверяют прочность и жесткость деталей рабочей клети. При назначении параметров режима прокатки (обжатий, натяжений, скоростей и т.д.) проверяют, не превышено ли в какой-либо клети максимально допустимое значение силы прокатки.

Согласно 3^му закону Ньютона, в контакте полосы и валка действуют две равные по величине, но противоположно направленные силы P_i: одна – со стороны бочки валка на прокатываемую полосу, другая – со стороны полосы на бочку валка. Если решают задачу напряженно-деформированного состояния полосы, под силой прокатки подразумевают силу, действующую на полосу со стороны валка. Если рассчитывают рабочую клеть на прочность и жесткость, под силой прокатки подразумевают силу, действующую на каждый валок со стороны полосы.

Исходя из определения силы прокатки, ее общую формулу можно записать в виде:

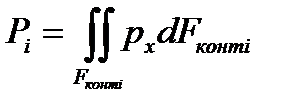, (8.1)

где знаком 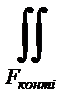обозначен двойной (поверхностный) интеграл по площади контакта полосы и валков i-й рабочей клети (F_контi) функции, выражающей распределение по этой площади переменных контактных нормальных напряжений p_x.

Однако на практике в инженерных расчетах силу прокатки определяют по упрощенной формуле:

, (8.2)

где p_срi – среднее значение нормального контактного напряжения в очаге деформации i-й рабочей клети;

F_контi – площадь контакта каждого валка i-й клети с полосой.

Смысл формулы (8.2) заключается в том, что в формулу (8.1), вместо переменных значений p_x, меняющихся по длине очага деформации и по ширине полосы, подставляют одно постоянное значение p_срi, равное средней величине p_x для всей площади контакта. Таким образом, p_срi – это своего рода равнодействующее напряжение, вызывающее появление такой же силы прокатки, как совокупность переменных контактных напряжений.

Подстановка в формулу (8.1) значения p_x= p_срi дает формулу (8.2).

Чтобы применять ее на практике, необходимо изучить методы определения каждого ее сомножителя - p_срi и F_контi.

Из литературы по теории прокатки известны различные методы расчета величин p_срi и F_контi [1;2;3;4;6;9;10;11;12;15;16;27]. Подробное изложение методов, разработанных до 80^х годов 20 века, с примерами расчетов, дано в справочнике [23], опубликованном в 1986 году. Сведения о точности расчета силы прокатки с помощью этих методов в справочнике не приведены. Между тем, требуемая точность расчета (расхождение между рассчитанными и измеренными силами прокатки) – основной критерий, определяющий выбор той или иной методики.

Если расчет выполняют для проектно-конструкторских целей, высокая точность вычисления силы прокатки не требуется. Цель такого расчета – обеспечение необходимой прочности и жесткости деталей и узлов рабочей клети, для чего необходимо установить максимально допустимую силу прокатки. При этом возможную погрешность расчета обычно компенсируют введением коэффициента запаса прочности. В этом случае можно использовать любую известную методику расчета, хотя наибольшее распространение в инженерной практике получила методика А.И. Целикова и его учеников [1;2;6], подробно изложенная в учебном пособии одного из соавторов этой методики Г.С. Никитина, опубликованном в 2009 году [15].

Если расчет силы выполняется для разработки технологического процесса прокатки, для управления этим процессом, требования к точности этого расчета значительно выше, особенно при производстве тонких широких полос на современных непрерывных станах.

Это объясняется тем, что в последние десятилетия 20 века и в начале 21 века в мировом листопрокатном производстве повысились требования к точности размеров и плоскостности горячекатаных и холоднокатаных листов и обострилась энергетическая проблема, что потребовало разработки более точных методов настройки рабочих клетей на заданные параметры прокатки, а также расчета эффективных технологических режимов работы станов.

Это обусловило необходимость создания усовершенствованных методов расчета контактных напряжений и среднего удельного давления.

Достоверность и точность этих методов невозможно проверить на натурных моделях рабочих клетей, т.к. высокие скорости, температуры, обжатия, натяжения, характерные для широкополосных станов, в лабораторных условиях воспроизвести невозможно. Единственный способ оценки качества методики энергосилового расчета – сопоставление расчетных и измеренных сил прокатки и мощности главных двигателей на действующих станах.

Все это вызвало необходимость совершенствования известных методик и разработки таких методов расчета сил и мощности прокатки, которые обеспечивают минимально возможную погрешность.

Ниже, в п. 8.2, изложены эти методы, обоснованные в работах [5;25], в которых, приведены достоверные статистические данные о сопоставлении расчетных и измеренных сил прокатки. Указанные методики обеспечивают погрешность расчета в 2-5 раз меньшую, чем упомянутые известные методики.

Так же, как в работах А.И. Целикова, в новой методике принято, что уширение полосы отсутствует, контактные напряжения изменяются только по длине очага деформации, для их вычисления составляют и решают уравнение равновесия элементарного объема полосы в очаге деформации.

Основное отличие решений [5;25] состоит в том, что в упругих участках очага деформации, вместо уравнения пластичности, использовано уравнение, основанное на законах упругости. Кроме того, при горячей прокатке уточнены закономерности трения в зоне прилипания, занимающей от 83 до 99% длины очага деформации (эти отличия подробно изложены в главе 6).