Е) Анализ закономерностей распределения нормальных контактных напряжений по длине очага деформации
Приведенные в табл. 6.8 и 6.9 формулы px(hx) дают возможность проанализировать характер распределения контактных напряжений по длине очага деформации.
Ниже изложены результаты исследования контактных напряжений в очагах деформации 6ти клетевого ШПСГП “1700” при прокатке полосы толщиной 0,87 мм шириной 1000 мм [25] по реальному режиму, параметры которого указаны в табл. 6.10. Рассчитанные длины очагов деформации и их участков, а также максимальные значения px(hx) и px(hx=hН) приведены в табл. 6.11.
Таблица 6.10
Параметры режима горячей прокатки полосы из стали 1ПС
Размерами 0,9х1000 мм
| Клеть № | vi, м/с | hi-1, мм | hi, мм | μi | σ i-1, МПа | σ i, МПа | ε i, % | ε Σi, % |
| 1,03 | 24,9 | 10,15 | 0,56 | 0,48 | 59,2 | 59,2 | ||
| 2,37 | 10,15 | 3,95 | 0,375 | 0,48 | 0,81 | 61,08 | 84,14 | |
| 4,42 | 3,95 | 2,18 | 0,333 | 0,81 | 1,83 | 44,81 | 91,25 | |
| 6,82 | 2,18 | 1,71 | 0,373 | 1,83 | 1,97 | 21,56 | 93,13 | |
| 9,81 | 1,71 | 1,04 | 0,2 | 1,97 | 2,43 | 39,18 | 95,82 | |
| 11,74 | 1,04 | 0,87 | 0,3 | 2,43 | 32,3 | 16,35 | 96,51 |
Примечание: vi – скорость полосы на выходе из i-й клети, ε Σi – суммарное обжатие после i-й клети.
На рис. 6.17 показаны характерные распределения нормальных контактных напряжений в 1й, 3й, и 6й клетях при горячей прокатке полосы по указанному режиму.
Таблица 6.11
Структурные параметры очагов деформации рабочих клетей при горячей прокатке полосы из стали 1ПС размерами 0,9х1000 мм
| Клеть № | lci, мм | x1упр, мм | xпл, мм | x2упр, мм | 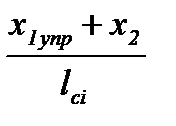 ,
% ,
%
| 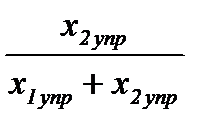 ,
% ,
%
| Xi | pxmax, МПа | pН, МПа | xН, мм |
| 0,1 | 70,3 | 0,51 | 0,86 | 0,76 | ||||||
| 0,07 | 45,2 | 0,71 | 1,7 | 0,68 | ||||||
| 0,07 | 24,4 | 1,18 | 4,9 | 0,61 | ||||||
| 0,09 | 12,5 | 1,19 | 9,2 | 0,57 | 920,5 | 919,6 | 0,5 | |||
| 0,06 | 14,8 | 1,65 | 10,4 | 0,59 | 0,36 | |||||
| 0,08 | 7,6 | 1,49 | 0,56 | 1293,7 | 1293,5 | 0,02 |
Примечания: Xi – показатель, характеризующий положение нейтрального сечения Xi=xпл.отст.xпл; pmax – максимальное значение контактных напряжений в очаге деформации; pН – значение контактных напряжений в нейтральном сечении; xН – расстояние от нейтрального сечения до сечения максимального нормального напряжения.
Анализ таблиц и рисунка дает основание для следующих выводов.
1. Доля упругих участков очага деформации от общей длины возрастает от 1-2% в первых клетях до 10-17% в последних клетях чистовой группы, что подтверждает целесообразность их учета в энергосиловом расчете широкополосных станов горячей прокатки. В первых клетях влияние упругих участков на величину усилий прокатки незначительно, но расчет контактных напряжений в этих участках позволяет достоверно определить величину напряжений в основной – пластической – зоне очага деформации.
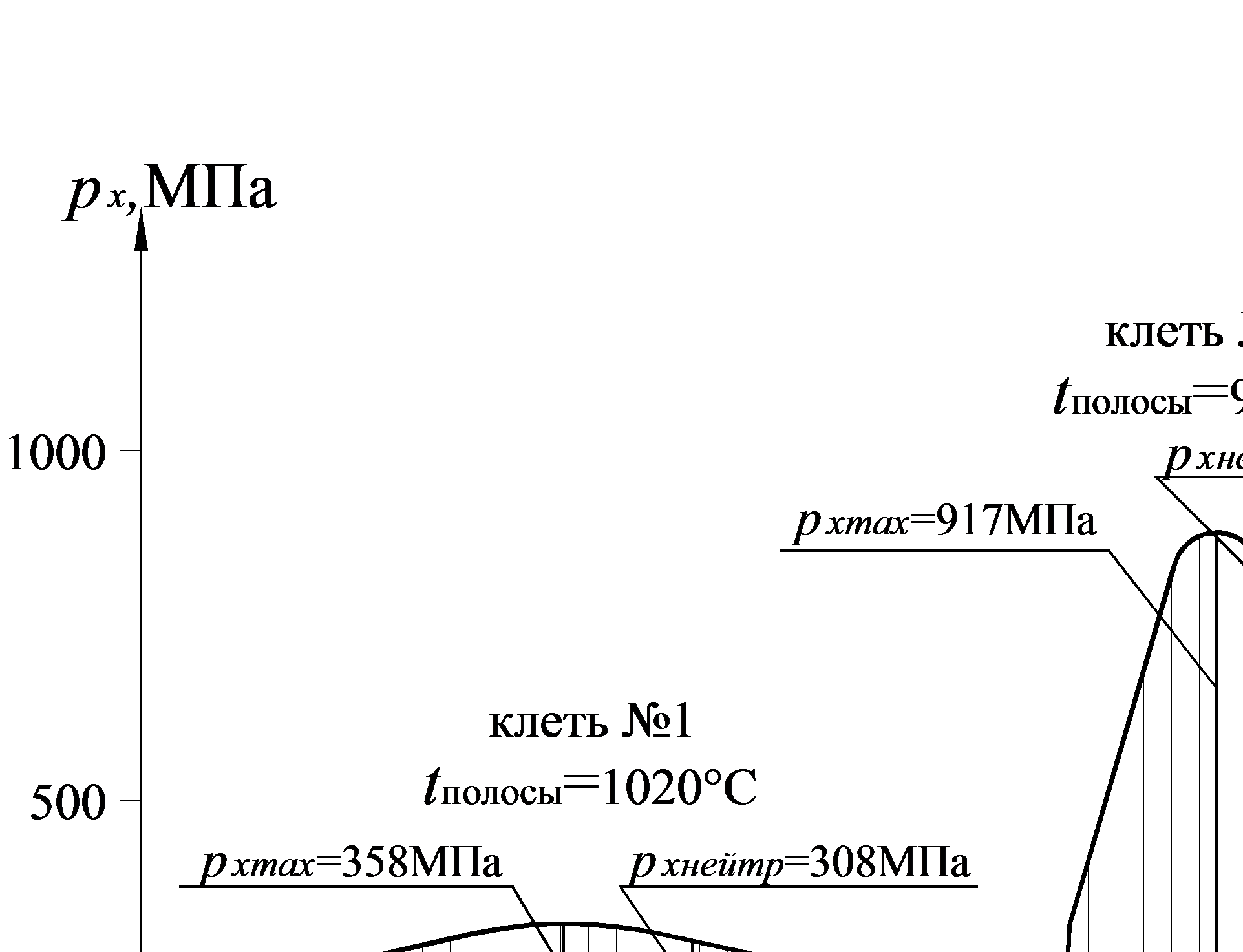
Рис. 6.17 Распределение нормальных контактных напряжений по длине очага
деформации в 1й, 3й и 6й клетях 6-клетевой непрерывной группы ШПСГП «1700»
(на примере прокатки полосы из стали 1ПС 24,9→0,9х 1000 мм)
2. Максимальные значения нормальных контактных напряжений увеличиваются от 350-500 МПа в первых клетях до 1300-1450 МПа в последних клетях, где они соответствуют уровню напряжений при холодной прокатке и оказывают большое влияние на интенсивность износа рабочих валков. Однако в первых клетях значительно выше температура полосы, что способствует выгоранию поверхности бочки валков, поэтому задача повышения стойкости рабочих валков при прокатке наиболее тонких полос актуальна для всех клетей чистовых групп широкополосных станов.
3. Нейтральное сечение не совпадает с сечением максимума контактных напряжений, особенно в первых клетях чистовой группы, где расстояние между этими сечениями составляют 11 мм. По мере уменьшения толщины полосы это расстояние уменьшается и в последних клетях нейтральное сечение почти совпадает с сечением максимума напряжений. На несовпадение этих сечений в зоне прилипания впервые указал А.И. Целиков [1;2]. Изложенная методика подтвердила эту особенность очага деформации и дала возможность достоверно рассчитать положение обоих сечений.
4. В отличие от холодной прокатки, где доля зоны отставания от общей длины пластических участков достигает 80-100%, при горячей прокатке эта доля находится в диапазоне 56-76%, то есть одно нейтральное сечение и зона опережения имеет место в очагах деформации всех рабочих клетей.
Примеры решения задач к главе 6[2]
Пример 1. Определить коэффициент трения в очаге деформации 2й рабочей клети 5-клетевого стана «1700» при холодной прокатке полосы из конструкционной стали.
Исходные данные: h1 = 1,38 мм, h2 = 1,08 мм, σ0,2(2) = 600 МПа, рср2 = 720 МПа, υ2 = 7 м/с, Ra исх= 0,6 мкм, τ = 3 часа.
Решение
| Рассчитываемые параметры | Обозна–чения | Расчетные формулы |
| 1. Среднеарифмети–ческая величина микронеровностей на поверхности бочки рабочих валков, мкм | Rа | Ra = Ra исх– 0,1141τ + 0,0064 τ2; Ra = 0,6 – 0,1141·3 + 0,0064· 32 = 0,32 |
| 2. Коэффициент трения. Формула (6.20) | μ2 | 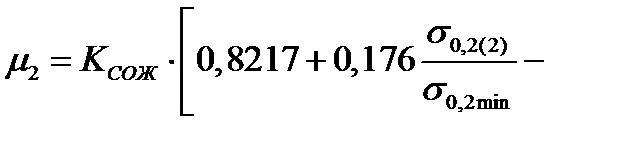 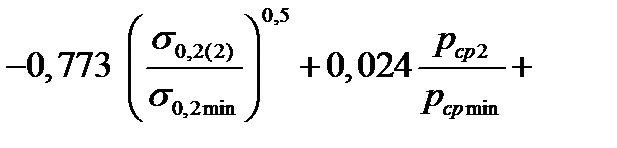
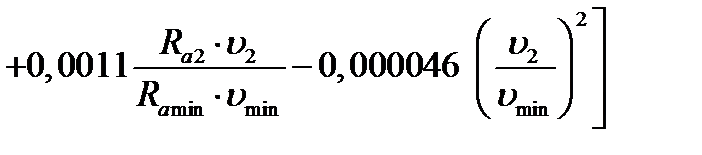 ; ;
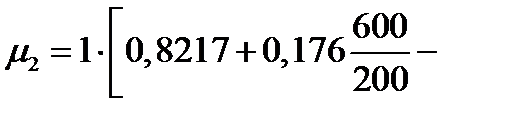
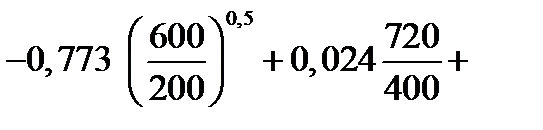
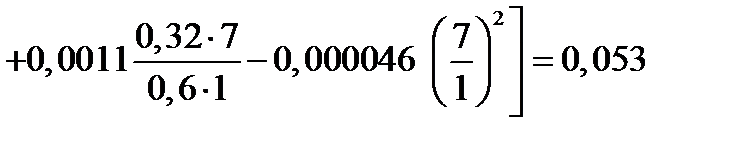
|
Пример 2. Определить средние значения сопротивления деформации для каждого участка очага деформации 1й рабочей клети 4-клетевого стана «1700» при холодной прокатке полосы из стали 20.
Исходные данные: h0 = 2,5 мм, h1 = 2,05 мм.
Решение
| Рассчитываемые параметры | Обозна–чения | Расчетные формулы |
| 1. Абсолютное обжатие, мм | Δh1 | 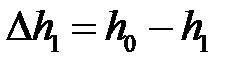 ; ;
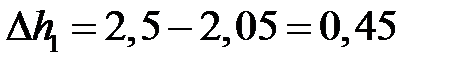
|
| 2. Суммарное относительное обжатие, % | εΣ1 | 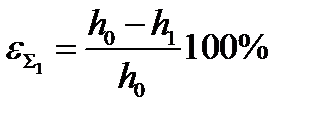 ; ;
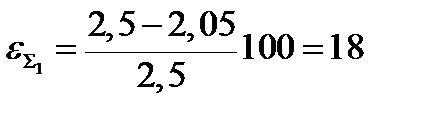
|
| 3. Эмпирические параметры | σ0,2исх, A, B | Определяем по справочным данным [23] для стали марки 20 σ0,2исх = 375 МПа; А = 31,6 МПа; В = 0,64 |
| 4. Условный предел текучести полосы на входе в клеть, МПа Формула (6.10) | σ0,2(0) | 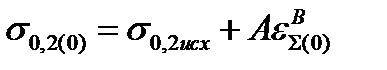 ; ;
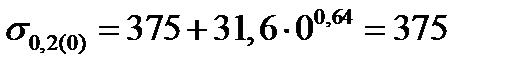
|
| 5. Условный предел текучести полосы на выходе из клети, МПа Формула (6.11) | σ0,2(1) | 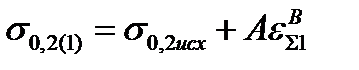 ; ;
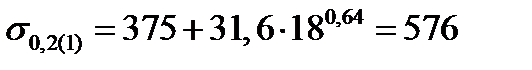
|
| 6. Среднее значение сопротивления деформации на пластическом участке, МПа Формула (6.19) | σф2 | 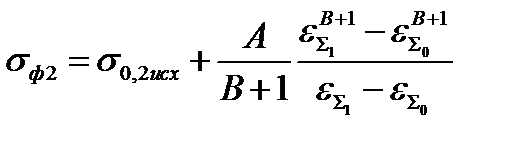 ; ;
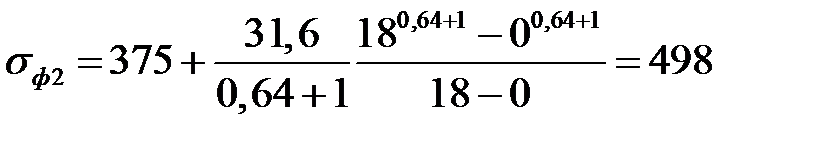
|
| 7. Среднее значение сопротивления деформации на участке упругого сжатия, МПа Формула (6.16) | σф1 | 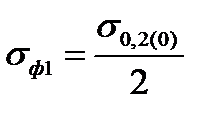 ; ;
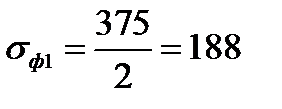
|
| 8. Среднее значение сопротивления деформации на участке упругого восстановления, МПа Формула (6.17) | σф3 | 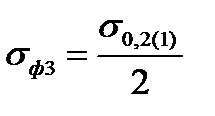 ; ;
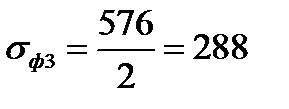
|
Пример 3. Рассчитать протяженности участков очага деформации 2й рабочей клети 6-клетевого стана «1700» при горячей прокатке полосы из стали 45.
Исходные данные: h1 = 10,8 мм, h2 = 5,2 мм, μ = 0,4, ЕП(Г) = 205000 МПа, ЕВ = 114000 МПа, νП = 0,3, νВ = 0,27, Dр = 630 мм, u = 2 c–1, t2 = 980 ºС.
Решение
| Рассчитываемые параметры | Обозна–чения | Расчетные формулы |
| 1. Абсолютное обжатие, мм | Δh2 | 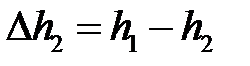 ; ;
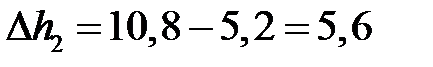
|
| 2. Частное относительное обжатие, % | ε2 | 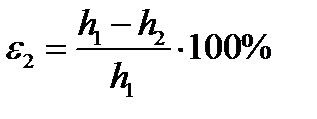 ; ;
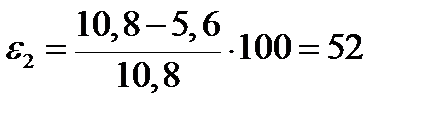
|
| 3. Эмпирические параметры | σод, S, a, b, c | Определяем по справочным данным [23] для стали марки 45: σод = 87,4 МПа; S = 1; a = 0,17; b = 0,13; c = –3,62 |
| 4. Среднее значение сопротивления деформации на пластическом участке. Формула (6.62) | σф2 | 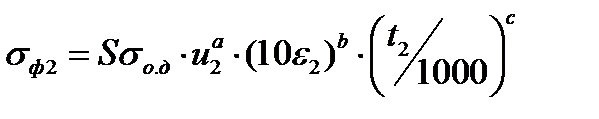 ; ;
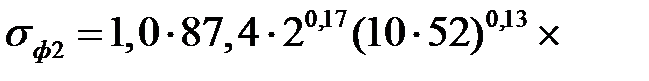 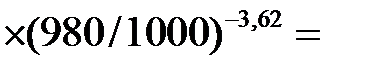 239 239
|
| 5. Максималь– ные величины абсолютных упругих деформаций полосы по толщине на участках с длинами х1упр и х2упр, мм. Формулы (6.70) | Δh1упр Δh2упр | 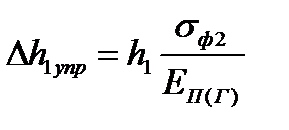 ; ;
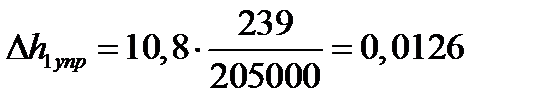 ; ;
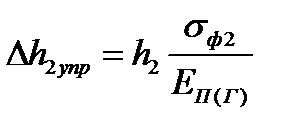 ; ;
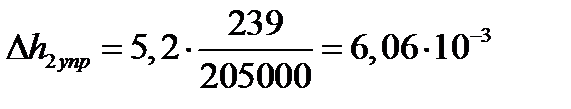
|
| 6. Среднее значение нормальных контактных напряжений без учета натяжений и упругих участков, МПа. Формула (6.42) | рср2’ | 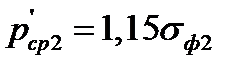 ; ;
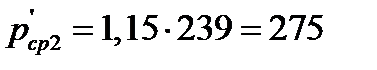
|
| 7. Длина участка упругого восстановления, мм. Формула (6.40) | х2упр | 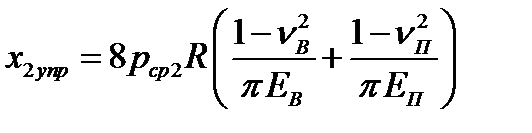 ; ;
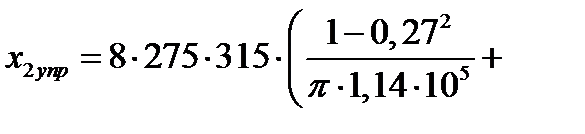 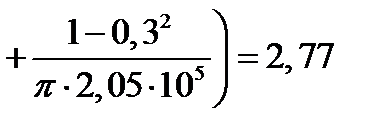
|
| 8. Длина упруго–пластического участка, мм. Формула (6.43) | х1 | 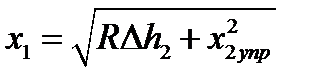 ; ;
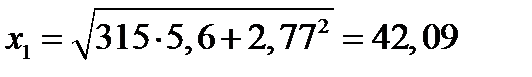
|
| 9. Длина очага деформации, мм. Формула (6.48) | lc2 | 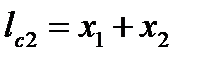 ; ;
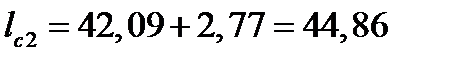
|
| 10. Длина участка упругого сжатия, мм. Формула (6.44) | х1упр | 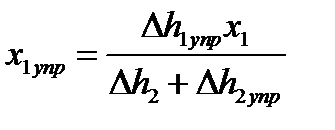 ; ; 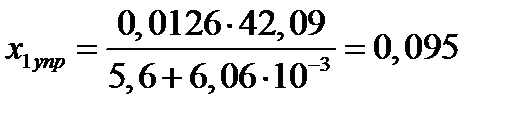
|
| 11. Длина пластического участка, мм. Формула (6.45) | хпл | 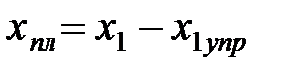 ; ;
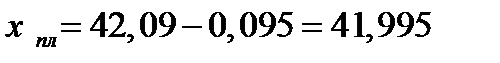
|
Дата добавления: 2019-02-08; просмотров: 1310;











