Расчет контактных напряжений в очаге деформации при горячей прокатке тонких широких полос

а) Основные допущения [25]

Горячую прокатку тонких широких полос производят в чистовых группах рабочих клетей широкополосных станов.

Как и при холодной прокатке, очаги деформации в этих клетях относятся к четвертому типу по классификации раздела 4 – низкие очаги, у которых соотношение .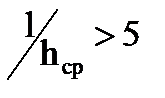

Поэтому некоторые из допущений, принятых для расчета контактных напряжений на станах холодной прокатки, используют и для горячей прокатки тонких широких полос (см. п. 6.3, а).

Первое из этих допущений.

Напряженное и деформированное состояние полосы считают плоскими, уширением пренебрегают, контактные напряжения – нормальные p_x и касательные τ_x – принимают постоянными по ширине, а сжимающие σ_x – постоянными и по ширине, и по толщине полосы в каждом сечении с координатой x в очаге деформации. Таким образом, эти напряжения считают функциями только одной переменной величины: толщины полосы h_x: p_x(h_x), τ_x(h_x), σ_x(h_x). Чем шире и тоньше прокатываемая полоса, тем в большей степени её реальное напряженно-деформируемое состояние соответствует указанному допущению. При прокатке широких полос (b ≥1000 мм) толщиной более 10 мм (например, в первой клети 6^ти клетевого ШПСГП “1700”, толщина полосы на входе h₀=25 мм, на выходе h₁=10-12 мм), строго говоря, в поперечных сечениях очага деформации сжимающие напряжения σ_x не постоянны по толщине. Однако насколько значительна неравномерность σ_x по толщине, измерить экспериментально невозможно, т.к. в условиях действующего стана подобные измерения нереальны, а в лаборатории создать условия, адекватные условиям промышленного процесса, также невозможно.

Поэтому допущение о постоянстве напряжений σ_x по толщине можно рассматривать как рабочую гипотезу, позволяющую получить инженерные формулы для расчета контактных напряжений в очагах деформаций и усилий прокатки в рабочих клетях ШПСГП.

О правомерности этой гипотезы можно судить путем сопоставления расчетных и измеренных усилий прокатки.

Согласно данным работы [25], использование этой гипотезы обеспечило диапазон погрешностей расчета усилий на ШПСГП 0,2-11,1% (среднее значение 4,8%). Для инженерных расчетов такие расхождения расчетных и измеренных усилий вполне приемлемы, тем более с учетом того обстоятельства, что другие известные методики расчета дают значительно бóльшие погрешности.

Второе допущение исходит из того, что угол захвата во всех рабочих клетях чистовой группы ШПСГП, кроме первой, не превышает 7-8^о, а в первой клети α≤10-12⁰. Следовательно, длина дуги контакта составляет 2-3% от длины окружности бочки рабочего валка. Поэтому дуга контакта полосы и валков, как и при холодной прокатке, может быть аппроксимирована прямыми отрезками AB и BC, как показано на рис. 6.2, а.

Третье допущение состоит в том, что при расчете напряжений, возникающих в очагах деформации рабочих клетей чистовых групп ШПСГП, необходимо, как и при холодной прокатке, учитывать специфику напряженного состояния полосы в упругих участках.

Особенно это важно при горячей прокатке наиболее тонких стальных полос (h=0,8-1,5 мм), которые ранее производили только на станах холодной прокатки. В последних клетях ШПСГП при производстве полос указанных толщин нормальные контактные напряжения достигают значений 1000-1400 МПа, характерных для процесса холодной прокатки. Это приводит к значительному взаимному упругому сплющиванию валков и полосы, в результате чего протяженность упругих участков увеличивается до 10-20% от общей длины очага деформации. Так как в этих участках не действует условие пластичности, контактные напряжения в них следует рассчитывать, заменив это условие на уравнения упругости (6.7) и (6.8), как это описано выше для упругих участков очага деформации процесса холодной прокатки.

Кроме указанных трех допущений, общих для процессов холодной и горячей прокатки тонких широких полос, при расчете контактных напряжений в очаге деформации ШПСГП принимают четвертое допущение, специфическое только для горячей прокатки. Оно касается изменения касательных напряжений τ_x между полосой и валками по длине очага деформации.

Этот вопрос проанализирован в п.5.3 главы 5, где показано, что бóльшую часть протяженности очага деформации рабочей клети ШПСГП занимает зона прилипания, в которой, вместо трения скольжения, между полосой и валками имеет место трение покоя, характеризуемое тем, что касательные напряжения τ_x зависят не от коэффициента трения скольжения, а от сопротивления чистому сдвигу материала полосы τ_S.

Точные координаты границ зоны прилипания определить сложно: эти координаты в каждом очаге деформации могут быть разными, в зависимости от величин обжатия, температуры полосы, уровня нормальных напряжений и т.д.

Однако, учитывая то обстоятельство, что и пластическая область, и зона прилипания занимают преобладающую часть длины очага деформации рабочей клети ШПСГП, можно принять в качестве рабочей гипотезы следующее четвертое допущение: при горячей прокатке границы зоны прилипания совпадают с границами пластической области очага деформации. Опыт показал, что указанное допущение не приводит к существенным расхождениям расчетных и измеренных усилий прокатки, т.е. практически не снижает точность энергосиловых расчетов ШПСГП, но существенно упрощает методику.

На основании этого допущения при расчете контактных напряжений приняты следующие схемы распределения по длине очага деформации скоростей полосы и касательных напряжений, являющихся по физическому смыслу напряжениями трения (см. рис. 6.16):

1. На первом упругом участке длиной x_1упр скорость поверхностного слоя полосы v_xпов меньше, чем окружная скорость бочки валка v_в. При этом величина v_xпов под воздействием напряжения трения τ_x со стороны валка, направленных вперед, увеличивается и в конце первого упругого участка (на границе с пластическим) достигает значения v_xпов=v_в. Таким образом, на всем протяжении первого упругого участка касательные напряжения изменяются по закону трения скольжения:

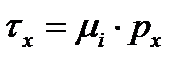, (6.59)

где μ_i – коэффициент трения скольжения;

p_x – нормальное контактное напряжение.

в)

б)

а)

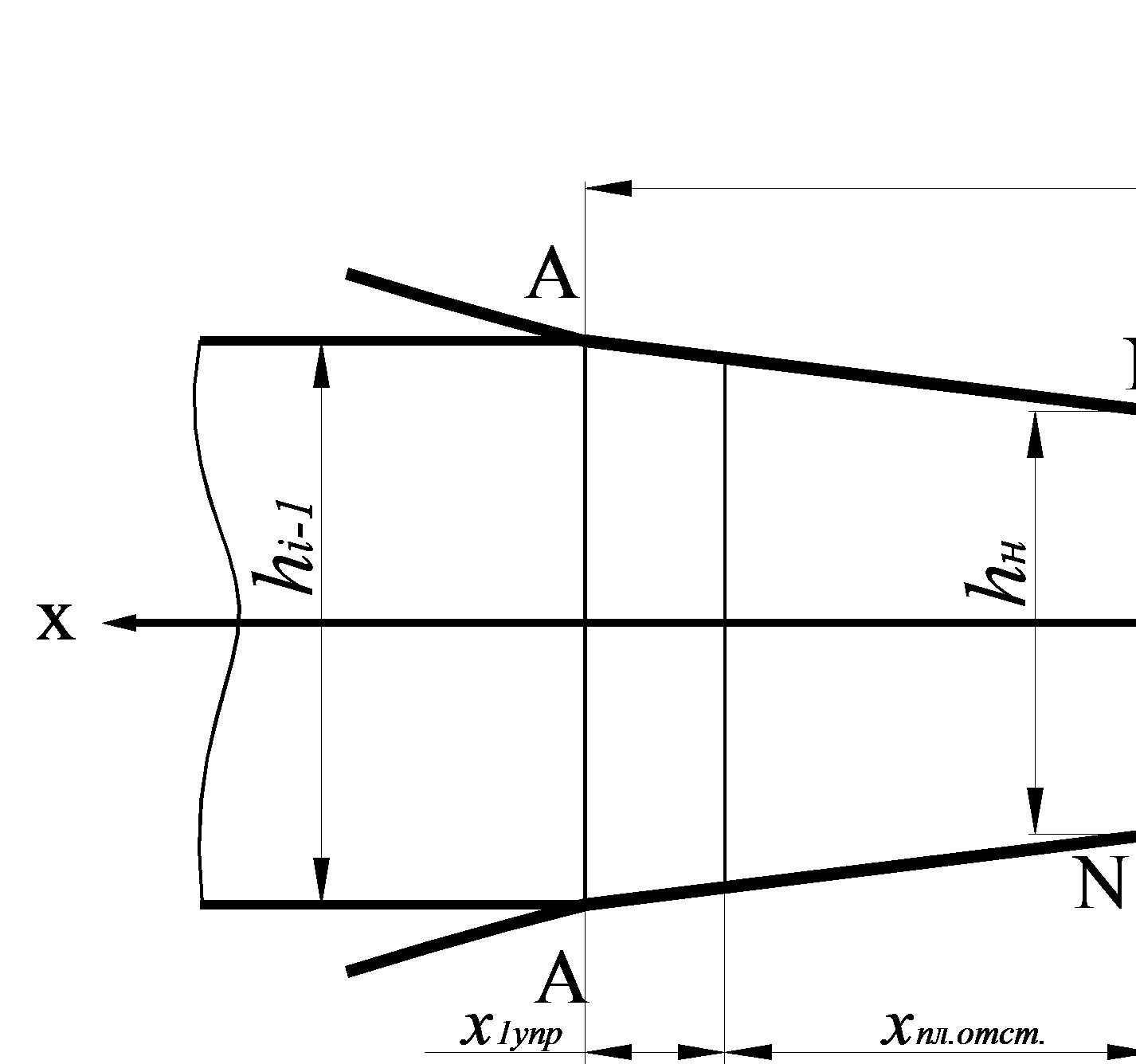
Рис. 6.16 Схема очага деформации i-ой рабочей клети (а), скорости полосы (б) и касательных напряжений между полосой и каждым валком (в), принятые в качестве допущений для расчета контактных напряжений при горячей прокатке тонких широких полос: ox – ось прокатки, h_i-1, h_i –толщина полоса на входе и на выходе, h_н – толщина полосы в нейтральном сечении, l_сi – длина очага деформации, x_1упр, x_2упр – длины 1^го и 2^го упругих участков, x_{пл.отст.}, x_{пл.опер.} – длины зон отставания и опережения пластического участка, v_в – окружная скорость бочки валков, v_i-1,v_i – скорость полосы на входе в i-ю клеть и выходе из нее, v_xпов – скорость поверхностного слоя полосы, v_xср – средняя по сечению скорость полосы, τ_x – касательные напряжения в контакте полосы с валками, τ_S – сопротивление чистому сдвигу материала полосы.

2. На границе между 1^м упругим и пластическим участками действие закона трения скольжения прекращается, т.к. τ_x достигло своего максимального значения: τ_x= τ_Si – сопротивления чистому сдвигу материала полосы.

По мере дальнейшего движения полосы вдоль пластического участка очага деформации напряжения трения изменяются в соответствии с закономерностями зоны прилипания, в которой трение скольжения перешло в трение покоя, характеризуемое отсутствием скольжения, т.е. равенством:

v_xпов=v_в. (6.60)

Однако средняя по сечению скорость полосы v_xср вдоль всего очага деформации непрерывно растет из-за обжатия, в соответствии с законом постоянства секундного объема (см. график “б” на рис. 6.16). В результате разность скоростей (v_в-v_xср) при движении полосы через очаг деформации изменяется согласно заштрихованной области на графике “б” рис. 6.16.

Логично допустить, что напряжения трения покоя τ_x(x) находятся в прямой зависимости от указанной разности скоростей, которая является своеобразным «скоростным напором», воздействующим на контактную поверхность полосы и валков.

Поэтому на пластическом участке, совпадающем с зоной прилипания, принято, что касательные напряжения изменяются линейно от максимального значения τ_xmax= τ_Si до минимального отрицательного значения τ_x≥- τ_Si, проходя через значение τ_x= 0 в нейтральном сечении, где скоростной напор равен нулю, в соответствии с выражением:

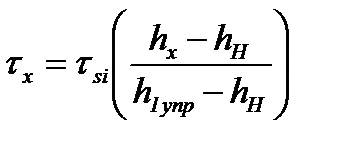, (6.61)

где h_Н – толщина полосы в нейтральном сечении;

h_1упр= h_i-1-Δh_1упр– толщина полосы на границе первого упругого и пластического участков;

h_i-1 – толщина полосы на входе в i-ю рабочую клеть;

- максимальная упругая деформацияполосы в конце первого упругого участка;

σ_ф.плi – среднее значение сопротивления деформации полосы на пластическом участке очага деформации i-й рабочей клети;

E_П – модуль упругости материала полосы.

Выражение (6.61) до нейтрального сечения характеризует изменение τ_x в зоне отставания, а после нейтрального сечения – в зоне опережения, где v_xср>v_в, а τ_x<0. Отрицательные значения τ_x имеют физический смысл, состоящий в том, что в зоне опережения напряжения трения направлены навстречу движению полосы (бочка валка, скорость которой в этой зоне меньше средней по сечению скорости полосы, силами трения притормаживает полосу).

3. На границе пластического и второго упругого участков зона прилипания, согласно принятому допущению, заканчивается, и на втором упругом участке вновь действует закон трения скольжения (6.59). При этом τ_x изменяется от минимального отрицательного значения до нуля.