Расчет контактных напряжений в очаге деформации при холодной прокатке тонких широких полос

А) Основные допущения

Для расчета контактных напряжений в очаге деформации при холодной прокатке тонких широких полос приняты следующие допущения, обоснованные в главах 2,5 и в п.п. 6.1, 6.2 данной главы[1]:

1. Напряженное и деформированное состояния полосы являются плоскими: уширение отсутствует, при этом в каждом поперечном сечении с осевой координатой x (см. рис. 6.2а) контактные напряжения – нормальное p_x и касательное τ_x – постоянны по ширине, а сжимающее напряжение σ_x постоянно и по толщине, и по ширине.

О

б)

а)

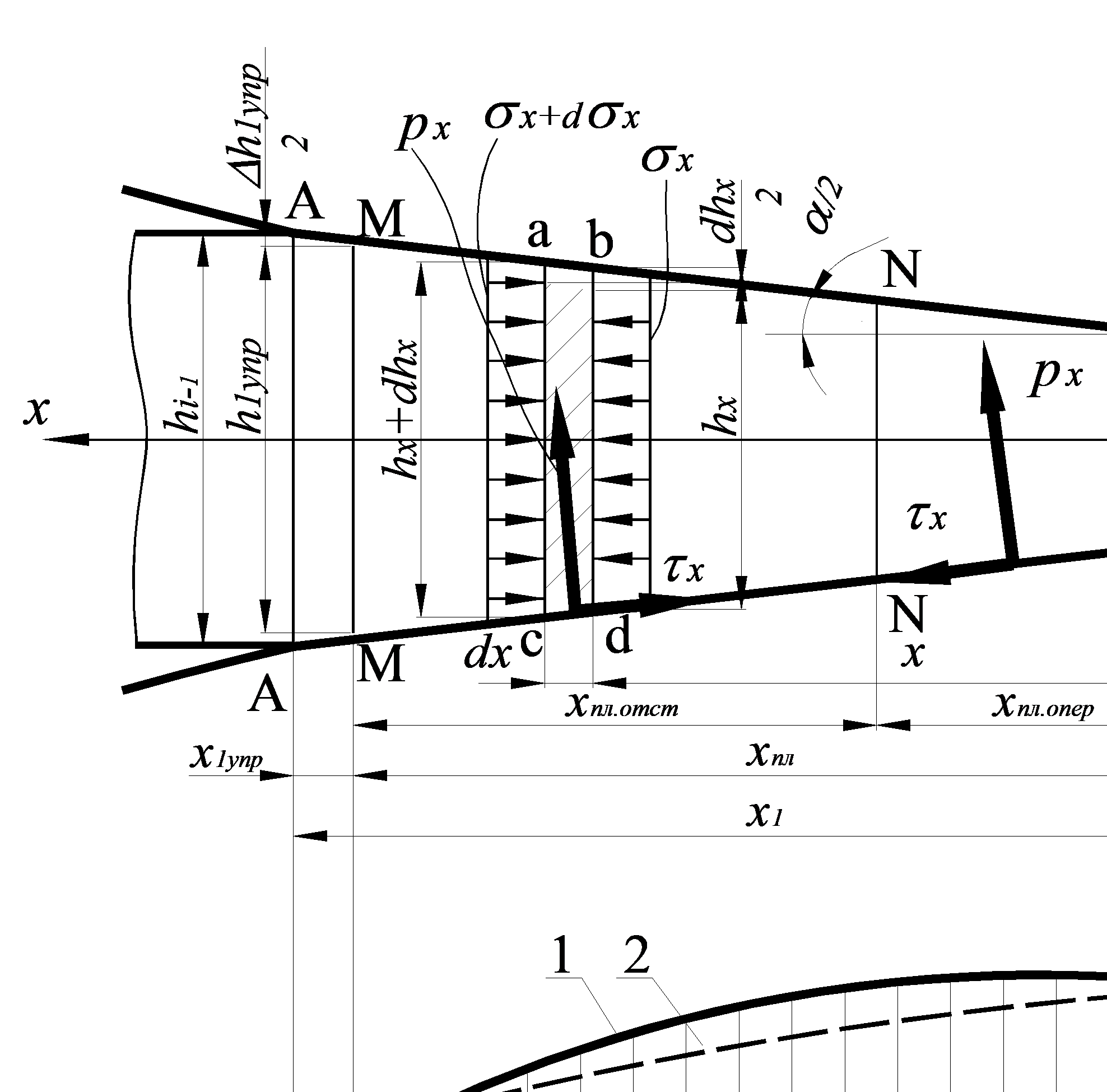
Рис. 6.2 Расчетные схемы для определения контактных напряжений

в очаге деформации при холодной прокатке

а: схемы очага деформации и контактных напряжений (NN – нейтральное

сечение), б) графики изменения сопротивления деформации

(1 – с учетом упругих участков, 2 – без учета упругих участков).

2. Зона прилипания в очаге деформации при холодной прокатке отсутствует, поэтому на всей его протяженности действует закон трения скольжения:

τ_x=μ p_x, (6.9)

где μ – коэффициент трения в очаге деформации, усредненный по площади контакта полосы и валка.

3. Дуги контакта полосы и валков, в связи с тем, что угол захвата α ≤4…5^о, аппроксимированы прямыми отрезками AB и BC, при этом очаг деформации состоит из следующих участков (см. схему, рис. 6.2а):

- участок упругого сжатия полосы длиной x_1упр;

- пластический участок длиной x_пл;

- участок упругого восстановления части толщины полосы длиной x_2упр.

4. На пластическом участке очага деформации напряженно-деформированное состояние полосы соответствует условию пластичности (6.2), а на упругих участках – уравнениям упругости (6.7), (6.8).

5. При холодной прокатке возможны три варианта структурных схем очага деформации (см. главу 5, рис. 5.1): с одним нейтральным сечением, с двумя нейтральными сечениями и без нейтральных сечений. Поэтому обязательным элементом расчета контактных напряжений в очаге деформации i-той рабочей клети стана холодной прокатки должно быть определение структурного варианта очага деформации.