Деформации и напряжения в металле при обработке давлением

Элементы теории пластической деформации

Общие положения

Теория пластической деформации (теория ОМД) – дисциплина, предшествующая дисциплине «теория прокатки» в учебных планах подготовки инженеров по специальности ОМД и бакалавров по направлению «металлургия» (профиль «ОМД».

Основные разделы теории ОМД и её взаимосвязь с другими дисциплинами учебного плана показаны на рис. 1.1 главы 1 «Введение».

В полном объеме теория ОМД изложена в ряде учебников и монографий, например, в работах [17…22]. В данной главе кратко изложены те элементы теории ОМД и законы пластической деформации, которые наиболее часто используются в теории прокатки, а также разъяснена сущность следующих понятий, являющихся базовыми как для теории пластической деформации, так и для теории прокатки:

- напряжения и силы, действующие между деформируемым металлом и инструментом;

- напряжения, возникающие внутри деформируемого металла;

- деформации, происходящие в металле под действием приложенных сил;

- сопротивление металла деформации и факторы, от которых оно зависит;

- условие пластичности;

- закономерности трения между металлом и инструментом;

- закон постоянства объема металла при пластической деформации.

Перечисленные элементы теории ОМД относятся к одному из её разделов: «механика пластически деформируемых тел». При пластической деформации происходят также сложные физические процессы, связанные с изменением структурных свойств обрабатываемых металлов. Эти процессы обычно изучают в других дисциплинах: «физика металлов», «материаловедение», «термическая обработка», «кристаллография», «текстурный анализ», поэтому в данном учебнике, как и в большинстве других учебников по теории прокатки, они не рассматриваются.

Одним из важнейших факторов, влияющих на величины напряжений и деформаций металла в процессе ОМД, является температура металла.

По признаку температуры процессы ОМД классифицируют на холодную пластическую деформацию (когда металл обрабатывают без предварительного нагрева, т.е. начинают процесс при температуре окружающей среды), горячую пластическую деформацию (когда до начала обработки металл нагревают до температур 1200^оС - 800^оС) и тёплую пластическую деформацию (диапазон температур 300^оС - 600^оС). Последний вид обработки характерен для пластической деформации цветных металлов и их сплавов, а горячей обработке подвергают сталь и её сплавы.

Деформации и напряжения в металле при обработке давлением

Для расчета энергосиловых параметров любого процесса ОМД и формоизменения металла в этом процессе необходимо определить напряжения и деформации, возникающие в металле под воздействием инструмента. Совокупность напряжений, действующих в объеме деформируемого металла и на его внешних границах, называют напряженным состоянием.

Совокупность деформаций, происходящих в каждой точке металла во время его обработки давлением, называют деформированным состоянием. Если одновременно рассматривают напряжения и деформации при обработке давлением, то применяют термин «напряженно-деформированное состояние».

2.2.1 Характеристики процессов деформации

Чтобы вести расчет процессов ОМД, используют ряд количественных характеристик этого процесса. Ниже указаны характеристики, чаще всего используемые в расчетах процессов прокатки.

а) Относительная деформация в заданном направлении (например, в направлении оси «Х»):

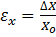(безразмерная) (2.1.а)

или 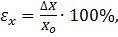(2.1.б)

где Х_о – первоначальный размер в направлении оси Х;

Х₁ - размер в направлении оси Х после деформации;

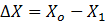– разность между первоначальным размером и размером после деформации (абсолютная деформация), мм.

б) Коэффициент деформации в заданном направлении (отношение размера после деформации к размеру до информации):

.

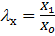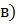Скорость деформации – производная относительной деформации по времени:

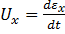, (2.2)

Где e_x берется в безразмерной форме по формуле (2.1.а).

Если формулу (2.1.а) применить к бесконечно малой абсолютной величине деформации dx, то: 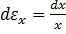. (2.3)

Подставив (2.3) в (2.2), получим:

.

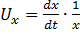Производная 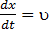[м/с] представляет собой линейную скорость изменения размера вдоль оси Х. Если вдоль оси Х происходит обжатие, то u_х - линейная скорость обжатия:

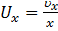. (2.4)

Из формул (2.2) – (2.4) видно, что более точно скорость деформации можно назвать скоростью относительной деформации. Размерность величины 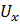, согласно формуле (2.4), 1/с.

Опыт исследований и расчетов процессов ОМД показал, что от скорости деформации зависят основные энергосиловые параметры этих процессов, поэтому в литературе [4; 17…24] приводятся формулы, по которым можно вычислить величину 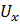или её среднее значение 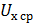. В частности, для процесса продольной прокатки авторы справочника [4] рекомендуют следующую формулу средней скорости деформации полосы по толщине при продольной прокатке (x = h):

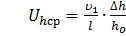(2.5)

где u₁ – скорость выхода полосы из валков, м/с;

l– длина очага деформации (зоны контакта полосы с валками), м;

h_o – толщина металла до прокатки, м;

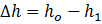– абсолютное обжатие, м;

h₁ – толщина металла после прокатки, м;

2.2.2 Напряженное состояние

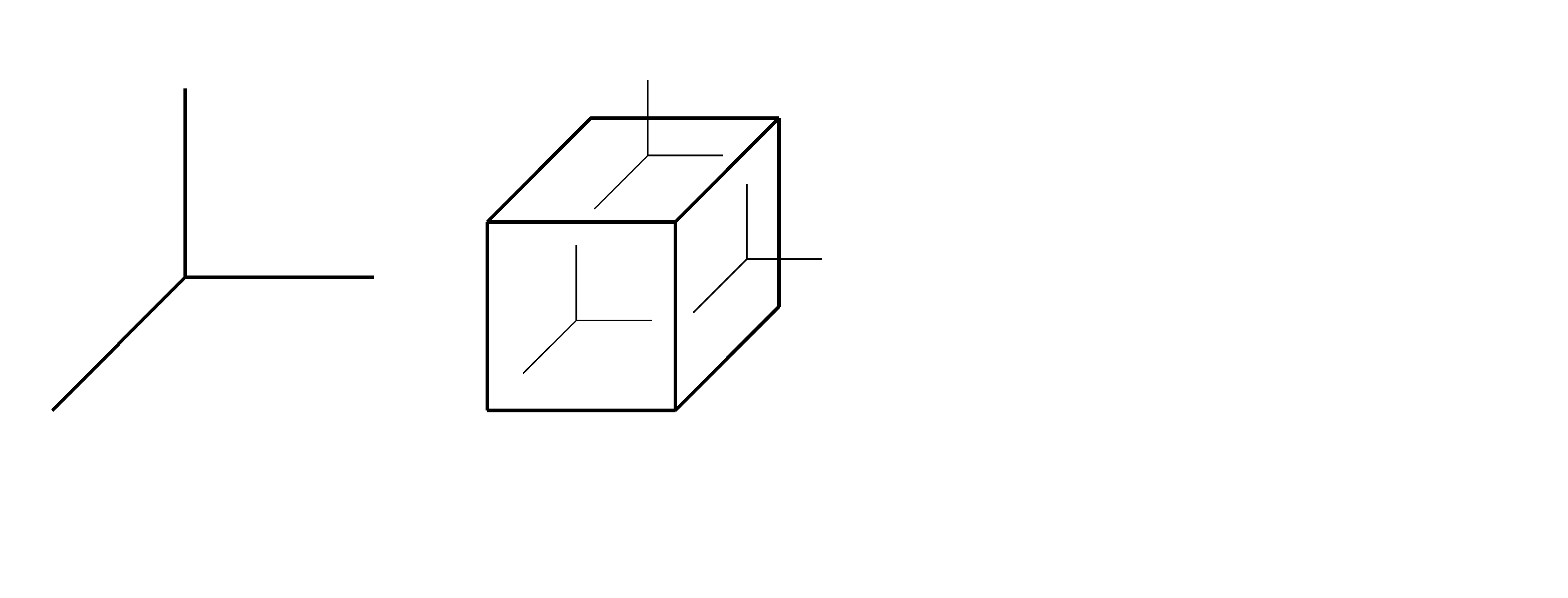
Так как напряжения могут быть разными в разных точках деформируемого тела, то, как и в теории упругости, для вывода расчетных формул напряжений в теории ОМД рассматривают бесконечно малый элементарный объем металла в виде кубика, грани которого расположены перпендикулярно координатным осям X,Y, Z (рис. 2.1).

z

y

x

τzy

σz

τzx

τxy

σx

τxz

σy

τyx

τyz

Рис. 2.1. Напряжения, приложенные к элементарному объему деформируемого металла

Напряжения, действующие на каждой грани элемента, показанного на рис. 2.1, являются векторами, направленными параллельно трём координатным осям. В реальном теле к каждой грани элементарного кубика приложено одно напряжение, направленное под некоторым углом к её поверхности. Однако для целей расчета эти напряжения разлагают на каждой грани по трем взаимно перпендикулярным направлениям, в результате получают три нормальных (s_х, s_y, s_z) и шесть касательных напряжений (t_xy и t_xz; t_yx и t_yz; t_zx и t_zy).

Эти напряжения оказывают на элемент разные механические воздействия: нормальные растягивают или сжимают его в направлении соответствующей оси, касательные представляют собой напряжения трения, вызванного воздействием поверхности соседнего элемента или инструмента.

В теории ОМД доказано, что касательные напряжения, действующие на- встречу друг другу на соседних гранях элементарного кубического объема, подчиняются закону парности:

t_xy = t_yx; t_yz = t_zy; t_xz = t_zx.

Таким образом, всего неизвестных компонентов напряженного состояния в каждой точке тела не девять, а шесть: три нормальных и три касательных. Эти компоненты напряженного состояния принято располагать в виде таблицы (матрицы):

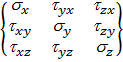. (2.6)

В первой строке этой таблицы расположены все компоненты напряжений, параллельные оси Х, во второй строке – параллельные оси Y, в третьей - параллельные оси Z. Кроме того, в первом столбце сгруппированы напряжения, действующие на площадке, нормаль к которой параллельна оси Х, во втором столбце – на площадке с нормалью, параллельной оси Y, и в третьем столбце – на площадке с нормалью, параллельной оси Z.

Матрицу (2.6) называют тензором напряжений. Он однозначно характеризует напряженное состояние в точке тела, вокруг которой расположен элементарный кубический объем, независимо от того, как выбраны направления координатных осей (т.е. под каким углом в пространстве повернуты грани кубика относительно стационарной системы координат). Больше того, среди бесконечного количества положений элементарного кубика всегда есть одно единственное, при котором на его гранях (площадках) отсутствуют касательные напряжения. Такие площади называют главными, а нормальные напряжения, действующие на главных площадках, называют главными нормальными напряжениями: s₁- максимальным, s₃ - минимальным, s₂ - промежуточным (s₁> s₂ >s₃). Как правило, для облегчения расчетов стремятся от произвольных напряжений, действующих параллельно и перпендикулярно координатным осям, перейти к главным нормальным напряжениям. Это делают для того, чтобы в конечном итоге определить одно напряжение, характеризующее напряженное состояние тела в точке: эквивалентное напряжение (s_экв).

Смысл величины s_экв. заключается в следующем. Реальное напряженное состояние металла, на который воздействует инструмент в процессе ОМД, может быть объемным (когда s₁ ¹ 0; s₂ ¹ 0; s₃¹0), плоским (когда одно из трех главных нормальных напряжений равно нулю) или (в редких случаях) – линейным (когда только одно из главных нормальных напряжений не равно нулю). Заменив с помощью математических преобразований, имеющихся в теории ОМД, три или два не равных нулю главных нормальных напряжений одним - величиной s_экв. -, мысленно заменяют реальное (объемное или плоское) напряженное состояние линейным, эквивалентным ему по степени нагруженности. Это позволяет изготовить круглый образец малого диаметра из того же материала, что и реальное тело, подвергаемое воздействию со стороны инструмента, и испытать его в лаборатории на растяжение или сжатие. Напряженное и деформируемое состояния такого образца во время испытания являются линейными, при этом легко определить области напряжений и деформаций, когда он находится в упругом и пластическом состояниях, и то значение напряжения (предел текучести (s_т) или сопротивление пластической деформации (s_ф), когда упругое состояние переходит в пластическое. Доведя испытание до разрушения образца, определяют также его предел прочности s_в. Поскольку степень нагружения образца напряжением s_обр. соответствует степени объемного или плоского нагружения реального тела напряжением s_экв в процессе ОМД, полученные при испытаниях образцов из разных металлов и сплавов значения s_т, s_ф, s_в используют для расчета напряжений и энергосиловых параметров в процессах ОМД реальных тел из тех же металлов и сплавов.

Для этого в теории ОМД получены специальные уравнения, связывающие напряжения реального процесса пластической деформации с величинами s_т, s_ф, измеренными при испытаниях образцов.

Эти уравнения называются условиями пластичности.