Условия пластичности

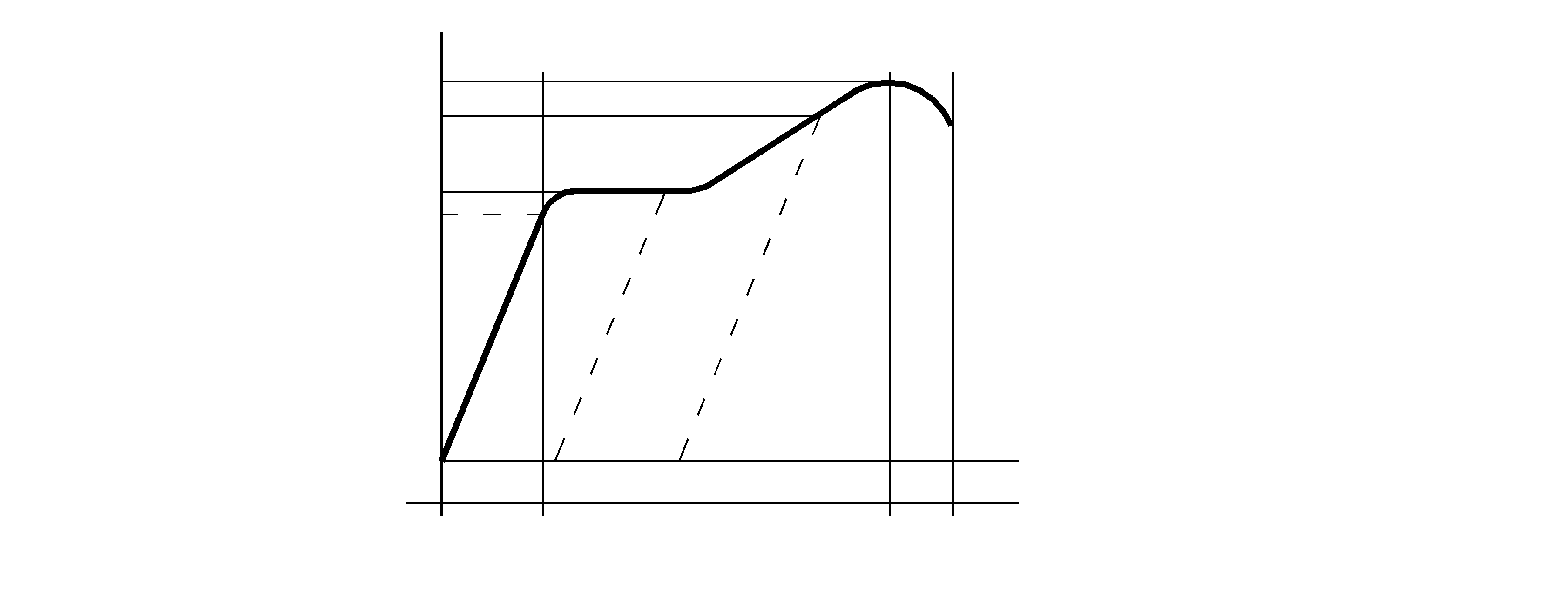
В теории ОМД известно несколько условий пластичности. Чтобы объяснить их смысл, лучше начать с условия пластичности для одноосного (линейного) напряженного состояния (когда образец с небольшой площадью поперечного сечения (например, круглый с диаметром 10-20мм) растягивают или сжимают, контролируя величины деформации и растягивающей (сжимающей) силы. Характерная диаграмма растяжения (сжатия) этого процесса показана рис. 2.2.

σ,

МПа

σВ

σф.исх

σф

σупр

а

b

β

c

e

εост1

εост2

ε, %

d

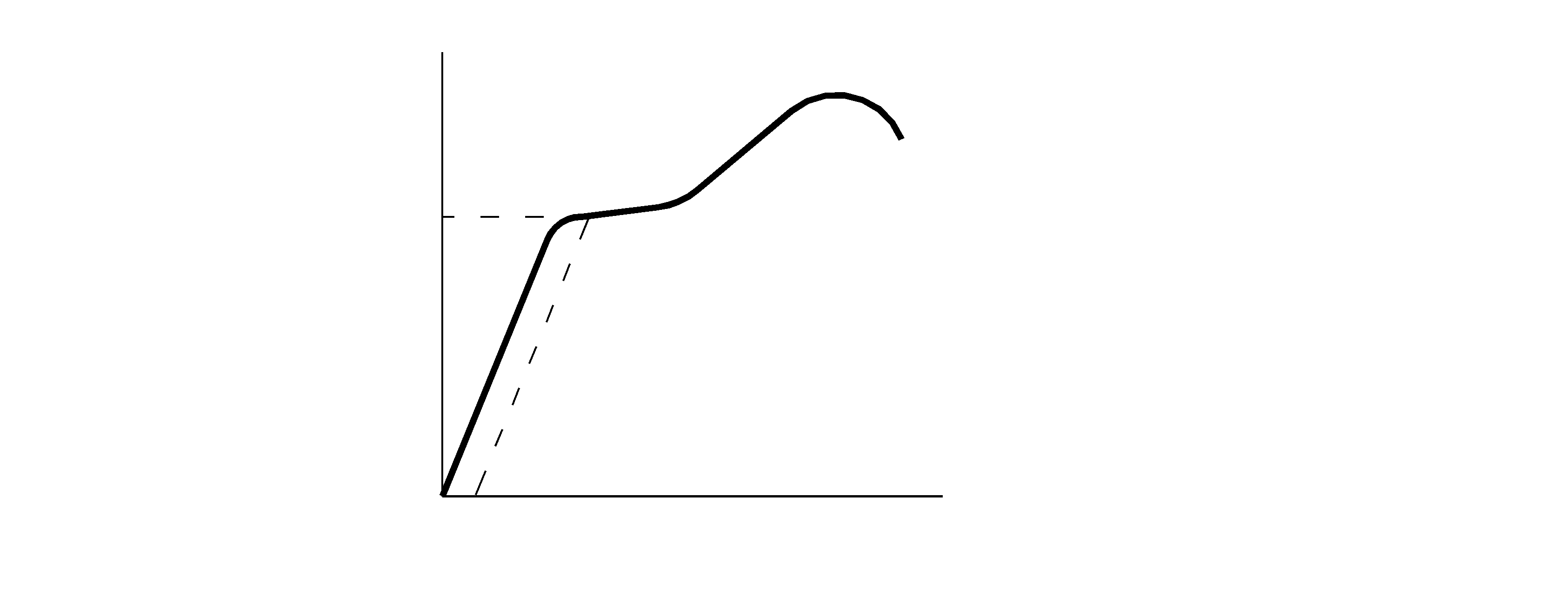
Рис. 2.2. Схематизированная зависимость растягивающего (сжимающего)

Напряжения от относительного удлинения (сжатия) при механическом

испытании образца металла.

По оси абсцисс этой диаграммы отложена относительная деформация по длине образца:

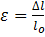(б/разм), или 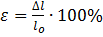, (2.7)

где l_o – первоначальная длина, м

Dl – абсолютное удлинение (сжатие), м.

По оси ординат отложено растягивающее (сжимающее) нормальное напряжение, направленное вдоль оси образца, перпендикулярно его поперечным сечениям:

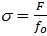, (2.8)

где F – осевая сила, растягивающая (сжимающая) образец, МН;

f_o – первоначальная площадь поперечного сечения образца, м².

На графике 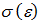видны три характерные зоны: упругой деформации (1), пластической деформации (2) и разрушения (3).

Напряжение s по своей сущности является сопротивлением деформации. В зоне 1 – это сопротивление упругой деформации, подчиняющееся одному из основных законов теории упругости – закону Гука:

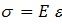, (2.9)

где 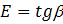- модель упругости материала образца.

Согласно (2.9), 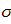прямо пропорционально 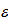, причем, если в любой точке графика в пределах зоны 1 прекратить нагружение (убрать силу F), то относительная деформация начнет уменьшаться по той же прямой (2.9), вплоть до нуля ( 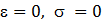), то есть, образец вернется к первоначальной длине (остаточная деформация e_ост = 0).

Поэтому зона 1 является штатной зоной работы деталей всех машин и механизмов. Максимальное значение 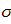в упругой зоне:

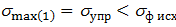(2.10)

где s_ф – начальное значение напряжения в пластической зоне 2 (исходное сопротивление пластической деформации материала образца).

Детали машин рассчитывают так, чтобы эквивалентное напряжение в наиболее нагруженных участках детали при работе машины подчинялось неравенству:

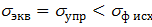, (2.11)

в котором значения s_упр и s_{ф исх} находят из диаграммы типа рис. 2.2, полученной путем механических испытаний образцов, изготовленных из того же материала, что и рассчитываемая деталь.

Выполнение для всех деталей машин условия (2.11) гарантирует надежную, без заклиниваний и поломок, работу машины.

Характерное принципиальное отличие деформации образца в зоне 2 состоит в том, что после прекращения нагрузки (растягивающей или сжимающей) образец не возвращается к первоначальному размеру. Например, если нагружение образца шло по линии о - а – b, то разгрузка его из точки «b» произойдет по прямой bс, параллельной оа, и при s = 0 его длина не будет прежней: сохранится остаточная деформация e_{ост 1} (отрезок ос на оси e).

При доведении нагрузки до точки «d» разгрузка произойдет по прямой dе и сохранится остаточная деформация .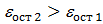

Смысл и задача любого процесса ОМД как раз и заключаются в целенаправленном изменении первоначальных размеров заготовки, т.е. в получении остаточной деформации. Напряжение s_{ф исх} на графике рис. 2.2, это такое напряжение, которое при увеличении деформации либо остается постоянным, либо увеличивается непропорционально величине относительной деформации.

Если испытания образца происходят при комнатной температуре, то

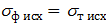, (2.12)

где s_{т исх} – исходный предел текучести (при условии, что образец не имел наклепа, вызванного предварительной деформацией)

Величина s_{т исх} используется для расчетов энергосиловых параметров процессов холодной пластической деформации. При горячей пластической деформации величина 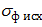зависит, кроме материала, от температуры и скорости деформации.

При увеличении нагрузки в пластической области сопротивление деформации увеличивается. Этот процесс называют наклепом металла (на графике рис. 2.2 величина ).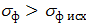

При механических испытаниях образцов из малопластичных (например, инструментальных) марок стали в холодном состоянии зависимость s(e) может несколько отличаться от кривой, показанной на рис. 2.2: на ней может отсутствовать горизонтальный участок.

Такая кривая показана на рис. 2.3.

Учитывая это, в расчетах процессах холодной прокатки, вместо понятия «предел текучести», используют понятие «условный предел текучести» s_0,2.

Это напряжение, после снятия которого в образце сохраняется остаточная деформация, равная 0,2%. Если на оси абсцисс графика рис. 2.3 отложить e = 0,2 % и из полученной точки провести прямую, параллельную первоначальной упругой, то пересечение её с кривой s(e) и даст значение s_0,2.

При испытании образца, который не подвергался предварительному наклепу, полученное значение s_0,2 равно его исходной величине: s_{0,2 исх} .

Таким образом, испытуемый образец оказывается в состоянии пластичности тогда, когда линейное напряжение s, создаваемое в нем внешними силами при известных условиях нагружения (относительной деформации e, температуре t, скорости деформации u) станет равным сопротивлению пластической деформации: s_ф.

σ

σ0,2

0,2

ε, %

Рис. 2.3. Диаграмма нагружения образца из малопластичной

стали (в холодном состоянии)

Следовательно, условие пластичности для линейного напряженного состояния имеет вид:

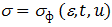(2.13)

Следует отметить, что влияние на сопротивление деформации величины относительной деформации и температуры противоположно. Если рост e вызывает увеличение s_ф из-за наклепа металла – искажения первоначальной формы зёрен, то рост t в диапазоне температур горячей пластической деформации (1200°С - 800°С) вызывает уменьшение s_ф из-за тенденции к восстановлению первоначальной (близкой к шаровой) формы зёрен – процесса, называемого рекристаллизацией. При горячей пластической обработке процессы наклёпа и рекристаллизации идут одновременно; какой из них преобладает – зависит от конкретных величин степени деформации и температуры.

Если фактическое напряжение 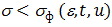, то металл находится в упругом состоянии. Если 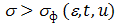, то металл подвергается опасности разрушения.

Смысл условия пластичности при объемном или плоском напряженном состоянии образца в реальном процессе ОМД заключается в том, что совокупность реальных напряжений в деформируемом теле под действием внешних сил сначала заменяют одним – эквивалентным – напряжением (s_экв), т.е. сводят реальное объемное (или плоское) напряженное состояние к аналогичному по степени загруженности линейному состоянию. Затем приравнивают s_экв величине s_ф, взятой из механических испытаний образца, изготовленного из того же материала и подвергнутого той же относительной деформации (e), при тех же условиях: температуре (t),скорости (u). Т.е. алгоритмически условие пластичности может быть представлено в виде ряда последовательных действий:

1. Переход от реального тензора напряжений, действующих на металл в процессе обработки давлением, к тензору, состоящему из главных нормальных напряжений.

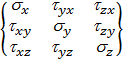
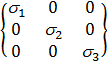. (2.14)

2. Переход от главных нормальных напряжений к эквивалентному напряжению.

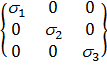s_экв. (2.15)

3. Составление условия пластичности в окончательном виде, аналогичного выражению (2.8):

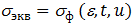(2.16)

При использовании выражений (2.14), (2.15) и (2.16) в расчетах процессов ОМД конкретный вид зависимости (2.14) главных нормальных напряжений от всего комплекса действующих напряжений устанавливают из анализа особенностей приложения внешних сил со стороны инструмента на деформируемое тело. Переход (2.15) от главных напряжений к эквивалентному производят по готовым формулам, имеющихся в теории пластичности. Таким образом, в левую часть условия пластичности (2.16) входит величина s_экв, выраженная через главные напряжения, действующие в реальном процессе ОМД, а в правую часть – справочная величина s_ф, полученная заранее при испытаниях образцов и не привязанная к конкретному процессу ОМД (главное, чтобы s_ф относилась к тому же материалу и к тем же условиям – температуре, степени и скорости деформации).

В теории ОМД известно несколько вариантов условия пластичности, конкретизирующих и объединяющих выражения (2.15), (2.16):

а) приближенная формула, известная как условие пластичности Сен-Венана:

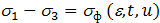. (2.17)

Это условие может давать погрешность до 16%, т.к. оно не учитывает влияние среднего главного нормального напряжений.

б) Более точная формула, учитывающая влияние среднего главного нормального напряжения:

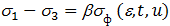. (2.18)

Коэффициент b называется коэффициентом Лоде, диапазон его значений: b= 1…1,15. Если среднее главное напряжение s₂ равно одному из двух других (s₂ = s₁ или s₂ = s₃), то b =1. Если 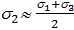, то b =1,15.

Именно такую величину b чаще всего используют в расчетах процессов ОМД, когда схема деформации плоская (например, при прокатке тонкой широкой полосы, когда отсутствует уширение).

При холодной пластической деформации в уравнения (2.17), (2.18), вместо s_ф, подставляют s_0,2. Более сложные выражения условий пластичности (для объемных схем деформации) приведены в литературе [17…22]. В практических инженерных расчетах их используют крайне редко.