Заболеваемость населения Н-ского района ветряной оспой за 10 лет
(на 10 000 населения)
| годы | ||||||||||
| показатель | 3,5 | 4,9 | 3,6 | 5,7 | 6,5 | 5,5 | 8,1 | 7,2 | 5,0 | 7,3 |
Задание: На основании данного динамического ряда требуется:
1. Обосновать необходимость выравнивания ряда.
2. Выровнять ряд по способу наименьших квадратов;
3. Рассчитать показатели динамического ряда (абсолютный прирост, темп прироста, средний темп прироста, значение 1% прироста);
4. Изобразить ряд графически;
5. Сделать выводы о динамике явления по выровненным уровням,
6. Охарактеризовать скорость изменения заболеваемости.
Решение
| Годы | Выравнивание по способу наименьших квадратов | Показатели динамического ряда | |||||||
| Уф факт. уровни | Х вре-мен. точки | Х2 | ХУ | УХ вырав-нен. уровни | абс. при-рост | темп при-роста в % | средний темп прироста | среднее значение 1% прироста | |
| 3,5 | - 9 | - 31,5 | 4,119 | -- | -- | Тпр.сн. = ((вхК) /а) х 100 = ((0,179х2) /5,73) х100 = 6,24 % | +0,358 = 6,24 = + 0,057 | ||
| 4,9 | - 7 | - 34,3 | 4,477 | +0,358 | 8,69 | ||||
| 3,6 | - 5 | - 18 | 4,835 | 7,99 | |||||
| 5,7 | - 3 | - 17 | 5,193 | 7,4 | |||||
| 6,5 | - 1 | - 6,5 | 5,551 | 6,89 | |||||
| 5,5 | + 1 | + 5,5 | 5,909 | 6,44 | |||||
| 8,1 | + 3 | + 24,3 | 6,267 | 6,05 | |||||
| 7,2 | + 5 | + 36,0 | 6,625 | 5,7 | |||||
| 5,0 | + 7 | + 35 | 6,983 | 5,4 | |||||
| 7,3 | + 9 | + 65,7 | 7,341 | 5,1 | |||||
| n = 10 | SУф. = 57,3 | SX=0 | S Х2 = 330 | S ХУ = 59,1 | S УХ = 57,3 |
а = S Уф. / n = 57,3 / 10 = 5,73 УХ 97 = 5,73 + 0,179 х (-9) = 4,119
в = S (Х Уфакт.) / S Х2 = 59,2 / 330 = 0,179 УХ 98 = 5,73 + 0,179 х (-7) = 4,477
УХ 99 = 5,73 + 0,179 х (-5) = 4,835
Абсолютный прирост выровненного ряда – 4,477-4,119 = 0,358
Темп прироста для 1997 г. = (0,358 / 4,119) х 100 = 8,69 %
Темп прироста для 1998 г. = (0,358 / 4,477) х 100 = 7,99 %
Темп прироста для 1999 г. = (0,358 / 4,835) х 100 = 7,4 %
Средний темп прироста = (0,179 х 2 / 5,73) х 100 = 6,24 %
Абсолютный прирост = 4,477 – 4,119 = + 0,358
Значение 1% прироста = + 0,358 / 6,24 = 0,057 %.
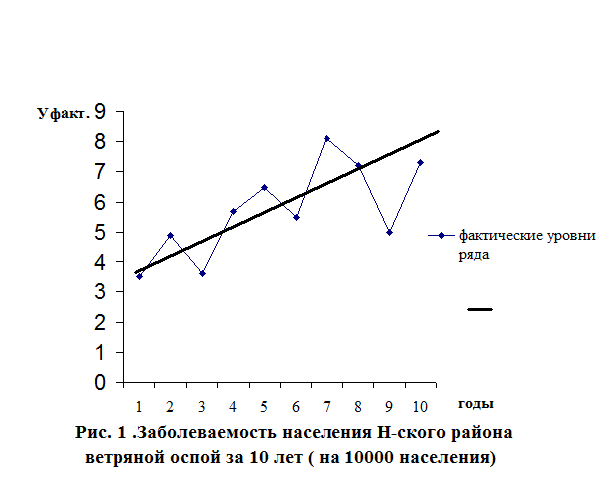
Выводы: Заболеваемость населения Н-ского района ветряной оспой за 10 лет неравномерна. Скорость изменений показателей заболеваемости различна, наибольший темп прироста отмечается в 1998 году. При выравнивании показателей динамического ряда отмечается тенденция к увеличению уровней заболеваемости, в среднем на 6,24 % ежегодно.
Контрольные вопросы
1. Дайте определение динамического ряда.
2. Какие Вы знаете типы динамических рядов?
3. Что такое преобразование динамического ряда?
4. Какие Вы знаете методы выравнивания динамического ряда?
5. Какой из методов выравнивания является боле точным?
6. Какие показатели свидетельствуют о скорости изменений уровней динамического ряда?
Тестовые задания
Выберите один или несколько правильных ответов:
1. Динамический ряд - это:
а) значения количественного признака (варианты), расположенные в определенном порядке и отличающиеся друг от друга по своему значению;
б) ряд, состоящий из однородных сопоставимых значений признака, характеризующих изменение какого-либо явления (процесса) во времени;
в) атрибутивные значения признака, характеризующие качественное состояние явления в динамике.
2. Динамический ряд может быть представлен:
а) абсолютными величинами;
б) средними величинами;
в) относительными величинами.
3. Способы выравнивания динамического ряда:
а) укрупнение интервалов;
б) расчет групповой средней;
в) вычисление скользящей величины;
г) метод наименьших квадратов.
4.Основными показателями скорости изменений явления в динамическом ряду являются:
а) темп роста;
б) абсолютный прирост;
в) темп прироста;
г) значение 1 % прироста;
д) средний темп прироста.
5. При сравнении нескольких динамических рядов с разными исходными уровнями необходимо рассчитывать показатель динамического ряда:
а) темп роста;
б) абсолютный прирост;
в) темп прироста;
г) значение 1 % прироста;
д) средний темп прироста.
6. С какой целью должно проводится выравнивание динамического ряда:
а) для выявления частоты распространения явлений или событий;
б) для установления тенденций при изучении явлений и процессов;
в) для доказательства влияния факторов;
г) для определения скорости изменения процесса.
7. Преобразование динамического ряда - это действия необходимые:
а) для установления тенденций за каждый период времени;
б) для установления тенденций по отношению к одному периоду, принятому за единицу (100%);
в) для установления закономерностей динамики процесса;
г) для выявления влияния факторов.
Ситуационные задачи
Задача 1
При анализе ежемесячной заболеваемости скарлатиной детей в возрасте до 7 лет в городе Н. в изучаемом году были получены следующие показатели динамического ряда: абсолютный прирост = + 0,5, темп прироста = +8,0%; темп роста = 7,0%.
1. По каким из представленных показателей можно судить о скорости изменения заболеваемости во времени?
2. Достаточно ли представленных в условии задачи данных для Вашего заключения о необходимости срочного планирования мероприятий по снижению заболеваемости скарлатиной на следующий год?
Задача 2
За последнее десятилетие отмечается увеличение числа выпуска врачей различного профиля в медицинских вузах №1 и №2, особенно увеличился выпуск в позапрошлом и прошлом годах.
Показатели динамики выпуска врачей вуза № 1 за последний год составили: абсолютный прирост = 50 человек, темп прироста = +8 %, а вуза № 2 за последний год - абсолютный прирост = 60 человек, темп прироста = 10 %.
1. Можно ли сделать вывод, что вуз № 2 более быстро решает проблему недостаточной численности подготовленных врачей? Какими показателями Вы воспользовались?
2. Достаточно ли представленных данных в условии задачи для суждения о приоритете в тенденциях по подготовке врачей в вузах?
Задача 3
В условиях реформирования здравоохранения в районах А. и Б. было проведено сокращение коечного фонда с увеличением при этом объема внебольничной помощи. 1% снижения (убыли) коечного фонда в районе А. составил 2 %, в районе Б. – 3%, а средний темп снижения (убыли) – соответственно– 5% и 7,5%.
1. В каком из районов сокращение коечного фонда идет быстрее. На основании какого показателя Вы сделали этот вывод?
2. Какие еще показатели дополнят анализ процесса сокращения коечного фонда в 2-х районах?
Задача 4
В городе Н. численность населения за последние 5 лет составляла в динамике:
1-й год - 100 00 человек, 2-й год - 90 000 , 3-й год - 80 000, 4-й год - 70 000 и 5-й год - 60 000 человек. Обеспеченность врачами за этот же период составила соответственно: 25, 23, 24, 18 и 20 на 10000 населения.
1. Являются ли исходные данные основой для составления динамического ряда и его последующего анализа?
2. Какие показатели динамического ряда необходимо рассчитать для углубленного анализа изменений численности населения и обеспеченности врачами?
Список литературы
Основная:
1.Власов В.В. Эпидемиология. - М.: ГЭОТАР-МЕД, 2004. - 464.
2.Лисицын Ю.П. Общественное здоровье и здравоохранение. Учебник для вузов. – М.:ГЭОТАР – МЕД, 2002.- 520 с.
3.Медик В.А., Юрьев В.К. Курс лекций по общественному здоровью и здравоохранению: Часть 1. Общественное здоровье. - М.: Медицина, 2003. - 368 с.
4.Социальная медицина и организация здравоохранения (Руководство в 2-х томах). Миняев В.А., Вишняков Н.И. и др. - СПб, 1998. - 528 с.
5.Социальная гигиена и организация здравоохранения (Учебное пособие). Кучеренко В.З., Агарков Н.М. и др. – Москва, 2000. – 432 с.
Глава 5. Дисперсионный анализ
Введение
В практической деятельности врачей при проведении медико-биологических, социологических и экспериментальных исследований возникает необходимость установить влияние факторов на результаты изучения состояния здоровья населения, при оценке профессиональной деятельности, эффективности нововведений.
Для определения влияния факторов существует ряд статистических методов, позволяющих определить силу, направление, закономерности влияния факторов на результат в генеральной или выборочной совокупностях (расчет критерия t, корреляционный анализ, регрессия, χ² (критерий согласия Пирсона) и др.).
Дисперсионный анализ был разработан и предложен английским ученым, математиком и генетиком Рональдом Фишером в 20-х годах XX века.
Дисперсионный анализ чаще используют в научно-практических исследованиях общественного здоровья и здравоохранения для изучения влияния одного или нескольких факторов на результативный признак, - он также устанавливает силу влияния фактора (ов) в выборочных совокупностях и основан на принципе «отражения разнообразий значений факторного(ых) на разнообразии значений результативного признака».
Сущность метода дисперсионного анализа заключается в измерении отдельных дисперсий (общая, факториальная, остаточная), и дальнейшем определении силы (доли) влияния изучаемых факторов (оценки роли каждого из факторов, либо их совместного влияния) на результативный (е) признак.
Цель изучения темы
На основе применения однофакторного дисперсионного анализа уметь оценивать силу и достоверность влияния фактора на результат.
По окончании изучения данной темы студент должен:
Уметь:
· обосновывать применение дисперсионного анализа в проводимом исследовании;
· проводить расчет показателей по этапам;
· на основании полученных данных проводить анализ полученных данных;
· формулировать практические выводы о влиянии факторов и их достоверности на состояние здоровья населения и /или деятельность учреждений здравоохранения.
Знать:
· основные понятия дисперсионного анализа;
· условия применения дисперсионного анализа;
· виды дисперсионного анализа;
· применяемые критерии для оценки полученных результатов.
Дата добавления: 2020-11-18; просмотров: 918;











