Методы корреляционного анализа
Ведение
При изучении общественного здоровья и здравоохранения в научных и практических целях исследователю часто приходится проводить статистический анализ связей между факторными и результативными признаками статистический совокупности (причинно-следственная связь) или определение зависимости параллельных изменений нескольких признаков этой совокупности от какой либо третьей величины (от общей их причины). Необходимо уметь изучать особенности этой связи, определять ее размеры и направление, а также оценивать ее достоверность. Для этого используются методы корреляции.
Цель изучения темы
На основе применения методов корреляции уметь выявлять влияние факторного признака на результативный при анализе общественного здоровья и деятельности медицинских учреждений, в том числе учреждений санитарно-эпидемиологического профиля.
По окончании изучения темы студент должен:
Уметь:
· устанавливать корреляционную зависимость методом квадратов и методом ранговой корреляции;
· оценивать силу, направление и достоверность полученного коэффициента корреляции и делать соответствующие выводы.
Знать:
· виды количественных связей;
· понятие о функциональной и корреляционной видах связи;
· практическое значение установления корреляционной связи;
· характеристики коэффициента корреляции (сила и направление связи);
· методы определения коэффициента корреляции (метод квадратов и ранговый метод);
· методические требования к использованию коэффициента корреляции;
· рекомендации по применению метода ранговой корреляции и метода квадратов;
· методику и порядок вычисления коэффициента корреляции по методу квадратов и методу ранговой корреляции, ошибок коэффициентов корреляции и способы оценки достоверности коэффициентов корреляции.
Задания для самостоятельной работы студента
1. Изучить материалы обязательной и рекомендуемой литературы, данного раздела учебного пособия.
2. Разобрать задачу-эталон.
3. Ответить на контрольные вопросы и тестовые задания в данном учебном пособии.
4. Решить ситуационные задачи.
Блок информации
| 1. Виды проявления количественных связей между признаками. | а) функциональная связь; б) корреляционная связь. | ||||
| 2. Определения функциональной и корреляционной связи. | Функциональная связь – такой вид соотношения между двумя признаками, когда каждому значению одного из них соответствует строго определенное значение другого (площадь круга зависит от радиуса круга и т.д.). Функциональная связь характерна для физико-математических процессов. Корреляционная связь – такая связь, при которой каждому определенному значению одного признака соответствует несколько значений другого взаимосвязанного с ним признака (связь между ростом и массой тела человека; связь между температурой тела и частотой пульса и др.). Корреляционная связь характерна для медико-биологических процессов. | ||||
| 3 Практическое значение установления корреляционной связи. | · Выявление причинно-следственной связи между факторными и результативными признаками (при оценке физического развития, для определения связи между условиями труда, быта и состоянием здоровья, при определении зависимости частоты случаев болезни от возраста, стажа, наличия производственных вредностей и др.). · Зависимость параллельных изменений нескольких признаков от какой-то третьей величины. Например, под воздействием высокой температуры в цехе происходят изменения кровяного давления, вязкости крови, частоты пульса и др. | ||||
| 4. Величина, характеризующая направление и силу связи между признаками. | Коэффициент корреляции, который одним числом дает представление о направлении и силе связи между признаками (явлениями), пределы его колебаний от 0 до ±1. | ||||
| 5. Способы представления корреляционной связи. | а) график (диаграмма рассеяния); б) коэффициент корреляции. | ||||
| 6. Направление корреляционной связи. | а) прямая; б) обратная. | ||||
| 7. Сила корреляционной связи. | а) сильная: ±0,7 до ±1; б) средняя: ± 0,3 до ±0,699; в) слабая: 0 до ±0,299. | ||||
| 8. Методы определения коэффициента корреляции и формулы. | а) метод квадратов (метод Пирсона); б) ранговый метод (метод Спирмена). | ||||
| 9. Методические требования к использованию коэффициента корреляции. | · измерение связи возможно только в качественно однородных совокупностях (например, измерение связи между ростом и весом в совокупностях, однородных по полу и возрасту); · расчет может производиться с использованием абсолютных или производных величин; · для вычисления коэффициента корреляции используются несгруппированные вариационные ряды (это требование применяется только при вычислении коэффициента корреляции по методу квадратов); · число наблюдений менее 30. | ||||
| 10. Рекомендации по применению метода ранговой корреляции (метод Спирмена). | · когда нет необходимости в точном установлении силы связи, а достаточно ориентировочных данных; · когда признаки представлены не только количественными, но и атрибутивными значениями; · когда ряды распределения признаков имеют открытые варианты (например, стаж работы до 1 года и др.). | ||||
| 11. Рекомендации к применению метода квадратов (метод Пирсона) | · когда требуется точное установление силы связи между признаками; · когда признаки имеют только количественное выражение. | ||||
| 12. Методика и порядок вычисления коэффициента корреляции. | 1) Метод квадратов
а) построить вариационные ряды для каждого из сопоставляемых признаков, обозначив первый и второй ряд чисел соответственно x и y;
б) определить для каждого вариационного ряда средние значения (М1 и М2);
в) найти отклонения (dx и dy) каждого числового значения от среднего значения своего вариационного ряда;
г) полученные отклонения перемножить
(dx х dy);
д) каждое отклонение возвести в квадрат и суммировать по каждому ряду ( Σ dx2 и Σ dy2);
е) подставить полученные значения в формулу раcчета коэффициента корреляции:
rxy 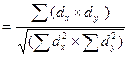
| ||||
при наличии вычислительной техники расчет производится по формуле:
rxy 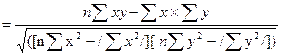
| |||||
2) Ранговый метод
а) составить два ряда из парных сопоставляемых признаков, обозначив первый и второй ряд соответственно х и у. При этом представить первый ряд признака в убывающем или возрастающем порядке, а числовые значения второго ряда расположить напротив того значения первого ряда, которым они соответствуют;
б) величину признака в каждом из сравниваемых рядов заменить порядковым номером (рангом). Рангами, или номерами, обозначают места показателей (значения) первого и второго рядов. При этом числовым значениям второго признака ранги должны присваиваться в том же порядке, какой был принят при раздаче их величинам первого признака. При одинаковых величинах признака в ряду ранги следует определять как среднее число из суммы порядковых номеров этих величин;
в) определить разность рангов между х и у (d)
d = х – у
г) возвести полученную разность рангов в квадрат (d2);
д) получить сумму квадратов разности (∑d2) и подставить полученные значения в формулу:
ρху 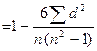
| |||||
| 13. Схема оценки корреляционной связи по коэффициенту корреляции | Сила связи | Направление связи | |||
| Прямая (+) | Обратная (–) | ||||
| Сильная | от +1 до +0,7 | от –1 до –0,7 | |||
| Средняя | от +0,699 до + 0,3 | от –0,699 до –0,3 | |||
| Слабая | от +0,299 до 0 | от –0,299 до 0 | |||
| 14. Вычисление ошибки коэффициента корреляции | а) Ошибка коэффициента корреляции, вычисленного методом квадратов (Пирсона):
mrxy 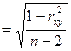
| |
б) Ошибка коэффициента корреляции, вычисленного ранговым методом (Спирмена):
mрxy 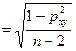
| ||
| 15. Оценка достоверности коэффициента корреляции полученного методом ранговой корреляции и методом квадратов | Способ 1
Достоверность определяется по формуле:
t= 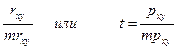
| |
| Критерий t оценивается по таблице значений t с учетом числа степеней свободы (n - 2), где n – число парных вариант. Критерий t должен быть равен или больше табличного; соответствующего вероятности р ≥99 %. Способ 2 Достоверность оценивается по специальной таблице стандартных коэффициентов корреляции. При этом достоверным считается такой коэффициент корреляции, когда при определенном числе степеней свободы (n - 2), он равен или более табличного, соответствующего степени безошибочного прогноза р ≥95 %. |
Задача-эталон на применение метода квадратов
Задание: Вычислить коэффициент корреляции, определить направление и силу связи между количеством кальция в воде и жесткостью воды, если известны следующие данные (таблица 4.6.1). Оценить достоверность связи. Сделать вывод.
Таблица 4.6.1
| Жесткость воды (в градусах) | Количество кальция в воде (в мг/л) |
Обоснование выбора метода. Для решения задачи выбран метод квадратов (Пирсона), т.к. каждый из признаков (жесткость воды и количество кальция) имеет числовое выражение; нет открытых вариант.
Решение
Последовательность расчетов изложена в тексте, результаты представлены в таблице. Построив ряды из парных сопоставляемых признаков, обозначить их через х(жесткость воды в градусах) и через у (количество кальция в воде в мг/л).
| Жесткость воды (в градусах) | Количество кальция в воде (в мг/л) | dx | dy | dx х dy | dx2 | dy2 |
| - 16 | - 114 | |||||
| - 12 | - 86 | |||||
| - 9 | - 66 | |||||
| + 7 | + 48 | |||||
| + 14 | + 98 | |||||
| + 16 | +120 | |||||
| Mx = Σx /n | Mу = Σу /n | Σdx Х dy= =7078 | Σ dx2 = 982 | Σ dy2 = 51056 | ||
| Mx =120 / 6=20 | Mу = 852 / 6 = 142 |
1. Определить средние величины Mx в ряду вариант «х» и Mу в ряду вариант «у» по формулам: Mx = Σx /n (графа 1) и Mу = Σу /n (графа 2).
2. Найти отклонение (dx и dy) каждой варианты от величины вычисленной средней в ряду «х» и в ряду «у»
dx = x - Mx (графа 3) и dy = у - Mу (графа 4).
3. Найти произведение отклонений dx х dy и суммировать их: Σ dx х dy (графа 5).
4. Каждое отклонение dx и dy возвести в квадрат и суммировать их значения по ряду «х» и по ряду «у»: Σ dx2 = 982 (графа 6) и Σ dy2 = 51056 (графа 7)
5. Определить произведение Σ dx2 х Σ dy2 и из этого произведения извлечь квадратный корень 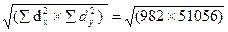 .
.
6.Полученные величины Σ (dx х dy) и 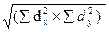 подставляем в формулу расчета коэффициента корреляции:
подставляем в формулу расчета коэффициента корреляции:
rxy 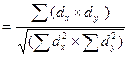 =
= 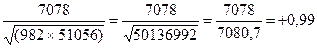 .
.
7. Определить достоверность коэффициента корреляции:
1 способ. Найти ошибку коэффициента корреляции (mrxy) и критерий t по формулам:
mrxy 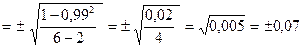
| t = | 0,99 | = 14,1 |
| 0,07 |
Критерий t = 14,1, что соответствует вероятности безошибочного прогноза р> 99,9 % .
2 способ. Достоверность коэффициента корреляции оценивается по таблице «Стандартные коэффициенты корреляции» (см. приложение 1). При числе степеней свободы (n – 2) = 6 – 2 = 4, наш расчетный коэффициент корреляции rxy = +0,99 больше табличного (r табл. = + 0,917 при р = 99 %).
Вывод: чем больше кальция в воде, тем она более жесткая (связь прямая, сильная и достоверная: rxy = + 0,99, р > 99,9 %).
Задача-эталон на применение рангового метода
Задание: методом рангов установить направление и силу связи между стажем работы в годах и частотой травм, если получены следующие данные:
| Стаж работы в годах | Число травм на 100 работающих |
| до 1 года | |
| 1 – 2 | |
| 3 – 4 | |
| 5 – 6 | |
| 7 и более |
Обоснование выбора метода: для решения задачи может быть выбран только метод ранговой корреляции, т.к. первый ряд признака «стаж работы в годах» имеет открытые варианты (стаж работы до 1 года и 7 и более лет), что не позволяет использовать для установления связи между сопоставляемыми признаками более точный метод – метод квадратов.
Решение
Последовательность расчетов изложена в тексте, результаты представлены в таблице 4.6.2:
Таблица 4.6.2
| Стаж работы в годах | Число травм | Порядковые номера (ранги) | Разность рангов | Квадрат разности рангов | |
| х | у | d (x-y) | d2 | ||
| до 1 года | - 4 | ||||
| 1 – 2 | - 2 | ||||
| 3 – 4 | 2,5 | + 0,5 | 0,25 | ||
| 5 – 6 | 2,5 | + 1,5 | 2,25 | ||
| 7 и более | + 4 | ||||
| Σ d2 = 38,5 |
1. Каждый из рядов парных признаков обозначить через «х» и через «у» (графы 1 – 2).
2. Величину каждого из признаков заменить ранговым (порядковым) номером. Порядок раздачи рангов в ряду «х» следующий: минимальному значению признака (стаж до 1 года) присвоен порядковый номер «1», последующим вариантам этого же ряда признака соответственно в порядке увеличения 2-ой, 3-ий, 4-ый и 5-ый порядковые номера – ранги (см. графу 3). Аналогичный порядок соблюдается при раздаче рангов второму признаку «у» (графа 4). В тех случаях, когда встречаются несколько одинаковых по величине вариант (например, в задаче – эталоне это 12 и 12 травм на 100 работающих при стаже 3 – 4 года и 5 – 6 лет, порядковый номер обозначить средним числом из суммы их порядковых номеров. Эти данные о числе травм (12 травм) при ранжировании должны занимать 2 и 3 места, таким образом среднее число из них равно (2 + 3)/2 = 2,5.
Таким образом, числу травм «12» и «12» (признак у) следует раздать ранговые номера одинаковые – «2,5» (графа 4).
3. Определить разность рангов d = (х – у) – (графа 5).
4. Разность рангов возвести в квадрат (d2 ) и получить сумму квадратов разности рангов Σ d2 (графа 6).
5. Произвести расчет коэффициента ранговой корреляции по формуле:
ρху 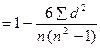 ,
,
где n – число сопоставляемых пар вариант в ряду «х» и в ряду «у».
ρху 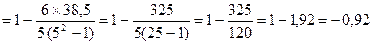
6. Определить достоверность коэффициента ранговой корреляции.
1 способ. Определить ошибку (mρxy) коэффициента ранговой корреляции и оценить достоверность его с помощью критерия t:
mρxy 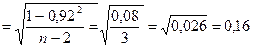
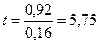
Полученный критерий t = 5,75 соответствует вероятности безошибочного прогноза (р) больше 95 %
ρxy = - 0,92 ; mρxy = ± 0,16 ; t = 5,75 ; р> 95 %
2 способ. По таблице «Стандартных коэффициентов корреляции»: при числе степеней свободы (n – 2) = 5 – 2 = 3 наш расчетный коэффициент корреляции ρxy = –0,92 больше табличного 0,878 и меньше 0,933, что соответствует вероятности безошибочного прогноза больше 95% и меньше 98%. Это позволяет считать полученный коэффициент ранговой корреляции достоверным.
Вывод: С вероятностью безошибочного прогноза (р) больше 95 % установлено, что чем больше стаж работы, тем меньше частота травм (связь обратная, сильная, достоверная корреляционная: ρxy = - 0,92, р> 95 %.
Контрольные вопросы
1. Дайте определение функциональной и корреляционной связи.
2. Приведите примеры прямой и обратной корреляционной связи.
3. Укажите размеры коэффициентов корреляции при слабой, средней и сильной связи между признаками.
4. В каких случаях применяется ранговый метод вычисления коэффициента корреляции?
5. В каких случаях применяется метод квадратов?
6. Каковы основные этапы вычисления коэффициента корреляции ранговым методом?
7. Каковы основные этапы вычисления коэффициента корреляции методом квадратов?
8. Как определяется достоверность коэффициента корреляции? Укажите способы.
Тестовые задания
Выберите один или несколько правильных ответов:
1. Укажите соответствие между видом связи и следующими примерами связи:
| Виды связи: 1. функциональная; 2. корреляционная. | Примеры: а) связь между температурой окружающей среды и температурой тела человека; б) зависимость пройденного расстояния больным с бронхиальной астмой от скорости его ходьбы, если продолжительность ежедневной прогулки постоянна; в) зависимость времени переливания больному 450 мл гемодеза от скорости падения капель при соблюдении стандартной технологии процедуры; г) зависимость между температурой окружающей среды и числом простудных заболеваний. |
2. Получить представление о силе и направлении связи между признаками можно с помощью:
а) таблиц, в которых записаны размеры признаков;
б) графического изображения зависимости;
в) коэффициента корреляции.
3. Направление корреляционной зависимости может быть представлено с помощью:
а) таблиц;
б) диаграмм рассеяния;
в) коэффициента корреляции.
5.Какому виду связи соответствуют следующие определения:
| Вид связи | Определения |
| 1. функциональная, 2. корреляционная. | а) каждому значению определенного признака соответствует несколько значений другого признака с ним взаимосвязанного; б) любому значению изучаемого признака соответствует строго определенное значение другого признака. |
Ситуационные задачи
Задача 1
В связи с ростом ревматизма в районе А. врач провел обследование семей жителей своего участка с целью выявления носителей стрептококковой инфекции в каждой семье. Врач Центра гигиены и эпидемиологии оценил санитарно-гигиеническую характеристику жилищных условий жителей этого участка.
| Жилищные условия | Носительство стрептококковой инфекции (на 100 обследованных) |
| Очень плохие Плохие Удовлетворительные Хорошие Наиболее благоприятные | 12, 0% 8, 0% 6, 0% 6, 0% 2, 0% |
1. Определите, какой метод позволит установить корреляцию между факторным признаком и результативным.
2. Обоснуйте свой вывод.
Задача 2
В городе Н. было проведено изучение зависимости заболеваемости инфарктом миокарда по месяцам года в зависимости от среднемесячной температуры воздуха
| Месяцы года | Заболеваемость инфарктом миокарда по месяцам (на 10 000 жителей) | Среднемесячная температура воздуха |
| январь февраль март апрель май июнь июль август сентябрь октябрь ноябрь декабрь | 1,6 1,23 1,14 1,13 1,12 1,02 0,91 0,82 1,06 1,22 1,33 1,4 | -7,1 -7,7 -5,8 -4,1 +13 +14,9 +18,8 +15,6 _+9,0 +6,0 -1,0 -7,7 |
1. Какой из методов следует применить для установления связи?
2. Обоснуйте свой вывод.
Задача 3
Между стажем работы ткачих и частотой понижения слуха у них установлена прямая корреляционная связь (rху= + 0,8). Ошибка коэффициента корреляции составила + 0,1.
1. Оцените коэффициент корреляции.
2. Какая дополнительная информация Вам необходима для оценки достоверности этой связи.
Задача 4
В научном исследовании между частотой материнской смертности и летальностью от внебольничного аборта установлена корреляционная зависимость.
1. Назовите факторные и результативные признаки.
2. Каким методом установлена связь в данной ситуации?
Задача 5
В трех районах города проводилось изучение заболеваемости кариесом детей в зависимости от содержания фтора в питьевой воде. При этом была установлена связь (rху = - 0,85).
1. Оцените силу и направление связи.
2. Можно ли утверждать, что при едином централизованном водоснабжении эта закономерность характерна для заболеваемости кариесом детей всего города?
3. Является ли условие задачи достаточным для Вашего утверждения?
Список литературы
Основная:
1. Власов В.В. Эпидемиология. - М.: ГЭОТАР-МЕД, 2004. - 464.
2. Лисицын Ю.П. Общественное здоровье и здравоохранение. Учебник для вузов. – М.:ГЭОТАР – МЕД, 2002.- 520 с.
3. Медик В.А., Юрьев В.К. Курс лекций по общественному здоровью и здравоохранению: Часть 1. Общественное здоровье. - М.: Медицина, 2003. - 368 с.
4. Социальная медицина и организация здравоохранения (Руководство в 2-х томах). Миняев В.А., Вишняков Н.И. и др. - СПб, 1998. - 528 с.
5. Социальная гигиена и организация здравоохранения (Учебное пособие). Кучеренко В.З., Агарков Н.М. и др. – Москва, 2000. – 432 с.
Дополнительная:
1. С. Гланц. Медико-биологическая статистика. Пер с англ. - М., Практика, 1998. –459 с. – С. 250-269.
Приложение 4.6.1
Дата добавления: 2020-11-18; просмотров: 776;











