Стандартные коэффициенты корреляции, которые считаются достоверными (по Л.С. Каминскому)
| Число степеней свободы – 2 | Уровень вероятности р (%) | ||
| 95 % | 98 % | 99 % | |
| 0,997 | 0,999 | 0,999 | |
| 0,950 | 0,980 | 0,990 | |
| 0,878 | 0,934 | 0,959 | |
| 0,811 | 0,882 | 0,917 | |
| 0,754 | 0,833 | 0,874 | |
| 0,707 | 0,789 | 0,834 | |
| 0,666 | 0,750 | 0,798 | |
| 0,632 | 0,716 | 0,765 | |
| 0,602 | 0,885 | 0,735 | |
| 0,576 | 0,858 | 0,708 | |
| 0,553 | 0,634 | 0,684 | |
| 0,532 | 0,612 | 0,661 | |
| 0,514 | 0,592 | 0,641 | |
| 0,497 | 0,574 | 0,623 | |
| 0,482 | 0,558 | 0,606 | |
| 0,468 | 0,542 | 0,590 | |
| 0,456 | 0,528 | 0,575 | |
| 0,444 | 0,516 | 0,561 | |
| 0,433 | 0,503 | 0,549 | |
| 0,423 | 0,492 | 0,537 | |
| 0,381 | 0,445 | 0,487 | |
| 0,349 | 0,409 | 0,449 |
4.7. Регрессионный анализ
Ведение
При наличии корреляционной связи между факторными и результативными признаками врачам нередко приходится устанавливать, на какую величину может измениться значение одного признака при изменении другого на общепринятую или установленную самим исследователем единицу измерения.
Например, как изменится масса тела школьников 1 класса (девочек или мальчиков), если рост их увеличится на 1 см. В этих целях применяется метод регрессионного анализа.
Наиболее часто метод регрессионного анализа применяется для разработки нормативных шкал и стандартов физического развития.
Цель изучения темы
На основе взаимосвязи между факторным и результативным признаками, выявленной методом корреляции, научиться измерять и анализировать изменения одного признака в зависимости от изменений другого при изучении общественного здоровья и деятельности лечебно-профилактических учреждений, в том числе учреждений Роспотребнадзора.
По окончании изучения темы студент должен:
Уметь:
· рассчитывать коэффициент регрессии, уравнение регрессии, сигму регрессии;
· на основе вычисленных параметров графически изображать линию и шкалу регрессии и делать соответствующее заключение.
Знать:
· определение регрессии и коэффициента регрессии,
· назначение коэффициента регрессии и уравнения регрессии,
· назначение сигмы регрессии,
· необходимые данные для расчета и графического изображения шкалы регрессии,
· практическое использование шкалы регрессии.
Задания для самостоятельной работы студента
1. Изучить материалы обязательной и рекомендуемой литературы, данного раздела учебного пособия.
2. Разобрать задачу-эталон.
3. Ответить на контрольные вопросы и тестовые задания в данном учебном пособии.
4. Решить ситуационные задачи.
Блок информации
| 1.Определение регрессии | Регрессия - функция, позволяющая по средней величине одного признака определить среднюю величину другого признака, корреляционно связанного с первым. С этой целью применяется коэффициент регрессии и целый ряд других параметров. Например, можно рассчитать число простудных заболеваний в среднем при определенных значениях среднемесячной температуры воздуха в осенне-зимний период. |
| 2. Определение коэффициента регрессии | Коэффициент регрессии – абсолютная величина, на которую в среднем изменяется величина одного признака при изменении другого, связанного с ним признака, на установленную единицу измерения. |
| 3. Формула коэффициента регрессии | 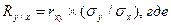 Ry/x - коэффициент регрессии,
rxy – коэффициент корреляции между признаками х и у .
(σy и σx) – среднеквадратические отклонения признаков х и у.
В нашем примере, rxy= - 0,96 (коэффициент корреляции между изменениями среднемесячной температуры в осенне-зимний период (х) и средним числом инфекционно-простудных заболеваний (у)),
Ry/x - коэффициент регрессии,
rxy – коэффициент корреляции между признаками х и у .
(σy и σx) – среднеквадратические отклонения признаков х и у.
В нашем примере, rxy= - 0,96 (коэффициент корреляции между изменениями среднемесячной температуры в осенне-зимний период (х) и средним числом инфекционно-простудных заболеваний (у)),
|
| σx = 4,6 (среднеквадратическое отклонение температуры воздуха в осенне-зимний период; σy = 8,65 (среднеквадратические отклонение числа инфекционно- простудных заболеваний), Таким образом, Ry/x – коэффициент регрессии Ry/x = –0,96 х (4,6 / 8,65) = 1,8, т.е. при снижении среднемесячной температуры воздуха (х) на 1 градус среднее число инфекционно- простудных заболеваний (у) в осенне-зимний период будет изменяться на 1,8 случаев. | |
| 4. Уравнение регрессии. | y = My + Ry/x (x–Mx), где: y- средняя величина признака, которую следует определять при изменении средней величины другого признака (x), x - известная средняя величина другого признака, Ry/x - коэффициент регрессии, Mx , My – известные средние величины признаков х и у . Например, среднее число инфекционно- простудных заболеваний (у) можно определить без специальных измерений при любом среднем значении среднемесячной температуры воздуха (х). Так, если х=–9˚, Ry/x = 1 8 заболеваний, Mx = –7˚, My = 20 заболеваний, то y = 20 + 1,8 х (9–7) = 20 + 3,6= 23,6 заболеваний. Данное уравнение применяется в случае прямолинейной связи между двумя признаками ( х и у). |
| 5. Назначение уравнения регрессии | Уравнение регрессии используется для построения линии регрессии. Последняя позволяет без специальных измерений определить любую среднюю величину (у) одного признака, если меняется величина (х) другого признака. По этим данным строится график – линия регрессии, по которой можно определить среднее число простудных заболеваний при любом значении среднемесячной температуры в пределах между расчетными значениями числа простудных заболеваний. |
| 6. Сигма регрессии (формула) | σ Ry/x = σу 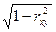 , где
σRy/x – сигма (среднеквадратическое отклонение) регрессии;
σу - среднеквадратическое отклонение признака у;
r ху – коэффициент корреляции между признаками х и у.
Так, если σу – среднеквадратическое отклонение числа простудных заболеваний = 8,65,
rху – коэффициент корреляции между числом простудных заболеваний (у) и среднемесячной температурой воздуха в осенне-зимний период (х) равен – 0, 96, то , где
σRy/x – сигма (среднеквадратическое отклонение) регрессии;
σу - среднеквадратическое отклонение признака у;
r ху – коэффициент корреляции между признаками х и у.
Так, если σу – среднеквадратическое отклонение числа простудных заболеваний = 8,65,
rху – коэффициент корреляции между числом простудных заболеваний (у) и среднемесячной температурой воздуха в осенне-зимний период (х) равен – 0, 96, то
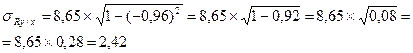
|
| 7. Назначение сигмы регрессии | Дает характеристику меры разнообразия результативного признака ( у). Например, характеризует разнообразие числа простудных заболеваний при определенном значении среднемесячной температуры воздуха в осеннне-зимний период. Так, среднее число простудниых заболеваний при температуре воздуха х1 = – 6˚ может колебаться в пределах от 15,78 заболеваний до 20,62 заболеваний. При х2 = – 9˚ среднее число простудных заболеваний может колебаться в пределах от 21,18 заболеваний до 26,02 заболеваний и т.д. Сигма регрессии используется при построении шкалы регрессии, которая отражает отклонение величин результативного признака от среднего его значения, отложенного на линии регрессии. |
| 8. Данные, необходимые для расчета и графического изображения шкалы регрессии. | а) коэффициент регрессии – Ry/x ; б) уравнение регрессии – y = My + Ry/x (x–Mx); в) сигма регрессии - σ Ry/x . |
| 9. Последователь- ность расчетов и графического изображения шкалы регрессии | а) определить коэффициент регрессии по формуле ( см. п. 3 блока информации). Например, следует определить, насколько в среднем будет меняться масса тела (в определенном возрасте в зависимости от пола), если средний рост изменится на 1 см. б) по формуле уравнения регрессии (см п.4 блока информации) определить, какой будет в среднем, например, масса тела ( у1 , у2 , ,у3…)* для определнного значения роста (х1 , х2 , х3 …). При этом средние значения массы тела и роста (Mx, и My) для определенного возраста и пола известны. в) вычислить сигму регрессии, зная соответствующие величины σу и r ху и подставляя их значения в формулу (см. п. 6 блока информации). г) на основании известных значений х1, х2, х3 и соответствующих им средних значений у1, у2, ,у3, а также наименьших (у – σRy/x) и наибольших (у + σRy/x) значений (у) построить шкалу регрессии. Для графического изображения шкалы регрессии на графике сначала отмечаются значения х1 , х2 , х3 (ось ординат), т.е. строится линия регресии, например, зависимости массы тела (у ) от роста (х). Затем, в соответствующих точках у1, у2, ,у3 отмечаются числовые значения сигмы регрессии, т.е. на графике находят наименьшее и наибольшее значения у1 , у2, у3. |
| 10. Практическое использование шкалы регрессии | Разрабатываются нормативные шкалы и стандарты, в частности, по физическому развитию. По стандартной шкале можно дать индивидуальную оценку развития детей. При этом физическое развитие оценивается как гармоничное, если, например, при определенном росте масса тела ребенка находится в пределах одной сигмы регрессии к средней расчетной единице массы тела – (у) для данного роста (х) (у ± 1 σRy/x). Физическое развитие считается дисгармоничным по массе тела, если масса тела ребенка для определенного роста находится в пределах второй сигмы регрессии (у ± 2 σRy/x). Физическое развитие будет резко дисгармоничным как за счет избыточной, так и за счет недостаточной массы тела, если масса тела для определенного роста находится в пределах третьей сигмы регрессии (у ± 3 σRy/x). |
Задача-эталон
По результатам статистического исследования физического развития мальчиков 5-ти лет известно, что их средний рост (х) равен 109 см, а средняя масса тела (у) равна 19 кг. Коэффициент корреляции между ростом и массой тела составляет + 0,9, средние квадратические отклонения представлены в таблице.
Требуется:
1) рассчитать коэффициент регрессии,
2) по уравнению регрессии определить, какой будет ожидаемая масса тела мальчиков 5-ти лет при росте, равном х1 = 100 см, х2 = 110 см, х3= 120 см;
3) рассчитать сигму регрессии и построить шкалу регрессии и результаты ее решения представить ее графически,
4) сделать соответствующие выводы.
Условие задачи и результаты ее решения представлены в сводной таблице. Этапы расчетов представлены в табл. 4.7.1.
Таблица 4.7.1
| Условия задачи | Результаты решения задачи | ||||||||
| Уравнение регрессии | Сигма регрес-сии | Шкала регрессии (ожидаемая масса тела (в кг)) | |||||||
| М | σ | r ху | Ry/x, | х | y | σ Ry/x | у – σRy/x | у + σRy/x | |
| Рост (х) | 109 см | ± 4,4 см | +0,9 | 0,16 | 100 см | 17,56 кг | ± 0,35 кг | 17,21 кг | 17,91 кг |
| Масса тела (у) | 19 кг | ±0,8 кг | 110 см | 19,16 кг | 18,81 кг | 19,51 кг | |||
| 120 см | 20,76 кг | 20,41 кг | 21,11 кг |
Решение
1) Коэффициент регрессии:
Ry/x = rxy х (σy/σx) = +0,9 х (0,8 / 4,4) = 0,16 кг/см.
Таким образом, при увеличении роста мальчиков 5 лет на 1 м масса тела увеличивается на 0,16 кг.
2) Уравнение регрессии:
y = My + Ry/x (x–Mx )
| х1 = 100 см х2 = 110 см х3 = 120 см | у1 = 19 + 0,16 (100-109) = 17,56 кг у2 = 19 + 0,16 (110-109) = 19,16 кг у3 =19 + 0,16 (120-109) =20, 76 кг |
3) Сигма регрессии:
σ Ry/x = σ у 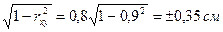
4) Шкала регрессии:
| рост | Среднее значение массы тела | Наименьшее значение массы тела | Наибольшее значение массы тела |
| х | y | у – σRy/x | у + σRy/x |
| 100 см 110 см 120 см | 17,56 кг 19,16 кг 20, 76 кг | 17,21 кг 18,81 кг 20,41 кг | 17,91 кг 19,51 кг 21,11кг |
5) Графическое изображение регрессии:
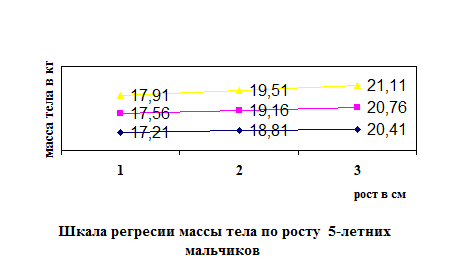
Вывод: Таким образом, шкала регрессии в пределах расчетных величин массы тела позволяет определить ее при любом другом значении роста или оценить индивидуальное развитие ребенка. Для этого следует восстановить перпендикуляр к линии регрессии.
Контрольные вопросы
1. Дайте определение «регрессии». В чем сущность метода регрессии?
2. Дайте определение коэффициента регрессии.
3. Какие данные нужно иметь, чтобы рассчитать коэффициент регрессии?
4. Какой можно сделать вывод, если коэффициент регрессии веса по росту равен 0,26 кг/см?
5. Для чего используется формула уравнения регрессии?
6. Для какой цели нужно рассчитать сигму регрессии?
7. Как построить и использовать шкалу регрессии физического развития
Тестовые задания
Выберите один или несколько правильных ответов:
1. Укажите правильное определение регрессии. Регрессия – это функция позволяющая …
а) по величине одного признака определить среднюю величину другого признака;
б) по средней величине одного признака определить среднюю величину другого признака, корреляционно связанного с первым;
в) определить, как количественно меняется одна величина при изменении другой, корреляционно связанной с ней, на единицу измерения.
2. Какая из ниже перечисленных величин применяется для определения размера одного признака при изменении другого на единицу измерения:
а) среднеквадратическое отклонение;
б) коэффициент корреляции;
в) коэффициент регрессии;
г) коэффициент вариации.
3. При изучении физического развития 5-летних девочек определена расчетным путем зависимость массы тела от роста (при росте 80 см, 85 см и 90 см).
Без специальных измерений массы тела можно определить ее величину при любом другом значении роста в границах от 80 см до 90 см.
С этой целью применяется:
а) коэффициент регрессии;
б) уравнение регрессии (линия регрессии);
в) шкала регрессии.
4. С помощью коэффициента регрессии можно определить:
а) без специальных измерений среднюю величину одного признака, зная среднюю величину другого;
б) абсолютную величину, на которую в среднем изменяется признак при изменении другого признака на установленную единицу измерения;
в) как количественно меняются величины одного признака по мере изменения величин другого признака.
5. Индивидуальная оценка физического развития детей и подростков проводится по:
а) линии регрессии;
б) шкале регрессии;
в) коэффициенту регрессии.
Ситуационные задачи
Задача 1
При изучении физического развития 7-летних мальчиков определена зависимость массы тела от роста (r ху = + 0,7).
1. Какой параметр необходимо рассчитать, для того чтобы можно было без специальных измерений массы тела определить, как будет меняться вес при изменении роста ребенка на 1 см.
2. Можно ли на основании имеющейся в условии задачи информации и названного Вами параметра построить шкалу регрессии?
Задача 2
В воздухе рабочей зоны одного из чехов предприятия при неисправной вентиляции среднее содержание пыли составляет 12 мг/м3. Заболеваемость болезнями органов дыхания рабочих возросла (r ху = + 0,7).
1. С помощью какого параметра можно определить, как будет меняться число заболеваний при увеличении количества пыли в воздухе рабочей зоны на 1 мг/м3?
2..Достаточно ли тогда будет данных условия задачи для построения уравнения регрессии?
Задача 3
В детском саду города Н. проводилось изучение физического развития детей старшего дошкольного возраста. При этом индивидуальные параметры роста и вес детей сильно различались.
1. С помощью какой методики врач оценивает индивидуальной развитие ребенка?
2. Какая величина позволяет конкретно оценивать гармоничность физического развития каждого ребенка?
Задача 4
При изучении распространенности гипертонической болезни у лиц в возрасте 40-49 лет был определен коэффициент регрессии , равный 3 мм. рт. ст.
1. Что означает коэффициент регресии?
2. Какова цель его практического применения в данном случае?
Задача 5
При проведении профилактических осмотров врач установил увеличение частоты сердечных сокращений студентов в зависимости от длительности нагрузки
(r ху = + 0,85).
1. Достаточно ли этого параметра для индивидуальной оценки частоты сердечных сокращений любого студента пришедшего на прием, в зависимости от дневной нагрузки?
2. Обоснуйте свой вывод.
Список литературы
Основная:
1. Власов В.В. Эпидемиология. - М.: ГЭОТАР-МЕД, 2004. - 464.
2.Лисицын Ю.П. Общественное здоровье и здравоохранение. Учебник для вузов. – М.:ГЭОТАР – МЕД, 2002.- 520 с.
3. Медик В.А., Юрьев В.К. Курс лекций по общественному здоровью и здравоохранению: Часть 1. Общественное здоровье. - М.: Медицина, 2003. - 368 с.
4. Социальная медицина и организация здравоохранения (Руководство в 2-х томах). Миняев В.А., Вишняков Н.И. и др. - СПб, 1998. - 528 с.
5.Социальная гигиена и организация здравоохранения (Учебное пособие). Кучеренко В.З., Агарков Н.М. и др. – Москва, 2000. – 432 с.
Дополнительная:
1. С. Гланц. Медико-биологическая статистика. Пер с англ. - М., Практика, 1998. –459 с. – С. 225-250.
Динамические ряды
Введение
В практической и научно-практической деятельности врачу нередко приходится анализировать происходящие во времени изменения в состоянии здоровья отдельных групп населения, в деятельности медицинских учреждений, в экспериментальных исследованиях. Выявление основой тенденции изучаемого явления вне влияния «случайных» факторов позволяет определять закономерности изменений явления и на этой основе осуществлять прогнозирование.
Цель изучения темы
На основании анализа уровней динамического ряда уметь делать выводы о закономерностях и тенденциях в состоянии здоровья населения и деятельности медицинских организаций и учреждений службы Роспотребнадзора.
По окончании изучения данной темы студент должен:
Уметь:
· обосновывать необходимость выравнивания динамического ряда, выбирать адекватный метод;
· выравнивать или преобразовать динамический ряд;
· представлять графически выровненный или преобразованный ряд;
· применять показатели изменений явлений для анализа динамического ряда;
· делать заключение о закономерностях изменений в изучаемом явлении или признаке.
Знать:
· определение и условия составления динамического ряда;
· типы рядов;
· методы выравнивания рядов и условия их применения;
· показатели изменений явлений в динамике, их назначение.
Дата добавления: 2020-11-18; просмотров: 731;











