Природа адсорбционных сил
Физическая адсорбция происходит под действием Ван-дер Ваальсовых сил межмолекулярного взаимодействия, которое складывается из ориентационных, индукционных и дисперсионных сил.
Ниже показана природа взаимодействия в зависимости от характера адсорбента и адсорбата. Полярным веществом называется вещество, обладающее интенсивным полем межмолекулярных сил.
| Адсорбент | Адсорбат | Силы взаимодействия |
| полярный полярный неполярный неполярный | полярный неполярный полярный неполярный | ориентационные индукционные дисперсионные |
Дисперсионные силы проявляются между мгновенными диполями, возникающими при сближении молекул за счет флуктуаций электронной плотности. Резонанс таких флуктуаций приводит к уменьшению общей энергии системы, обусловленному притяжением атомов. Потенциал межмолекулярного взаимодействия определяется выражением: 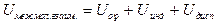 .
.
Если оценить вклад каждого из трех типов взаимодействий - ориентационного, индукционного и дисперсионного в общую энергию притяжения молекул, то оказывается, что доля индукционного эффекта составляет не более 5%. Доля ориентационного эффекта зависит от дипольных моментов взаимодействующих молекул. Для таких сильно полярных молекул, как аммиак и вода, ориентационный эффект равен дисперсионному. Следовательно, для неполярных и слабополярных молекул основным типом межмолекулярного взаимодействия является дисперсионное.
Различные виды межмолекулярного взаимодействия характеризуются одним и тем же законом изменения энергии притяжения от расстояния между молекулами 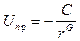 , где
, где 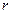 - расстояние между центрами атомов или молекул,
- расстояние между центрами атомов или молекул, 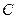 - константа, в которую входят характеристики молекул или атомов, соответствующие для каждого эффекта.
- константа, в которую входят характеристики молекул или атомов, соответствующие для каждого эффекта.
На очень близких расстояниях при перекрывании электронных оболочек атомов, возникает отталкивание, называемое борновским отталкиванием и описываемое эмпирическим соотношением:
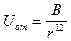
Полная энергия адсорбционного взаимодействия определяется уравнением Леннард-Джонса 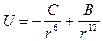 , где
, где 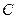 - константа межмолекулярного притяжения,
- константа межмолекулярного притяжения, 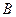 - константа борновского отталкивания, происходящего при перекрывании электронных орбит,
- константа борновского отталкивания, происходящего при перекрывании электронных орбит, 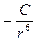 - энергия межмолекулярного (дисперсионного) притяжения,
- энергия межмолекулярного (дисперсионного) притяжения, 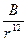 - энергия борновского отталкивания, которое происходит при малых
- энергия борновского отталкивания, которое происходит при малых 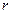 и обусловлено запретом Паули. Потенциал притяжения всегда отрицателен, а потенциал отталкивания - положителен.
и обусловлено запретом Паули. Потенциал притяжения всегда отрицателен, а потенциал отталкивания - положителен.
Межмолекулярные силы действуют на малых расстояниях порядка 10-9 м. При адсорбции дисперсионные силы действуют одновременно между молекулами адсорбата и поверхностью, т.е. многими атомами адсорбента. дисперсионные силы обладают свойством аддитивности, происходит суммирование адсорбционных сил, и суммарный потенциал адсорбции определяется выражением 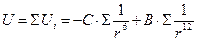 .
.
В результате суммирования парных взаимодействий, т. е. тройного интегрирования по объему адсорбента, степень 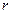 уменьшается, и межмолекулярное взаимодействие увеличивается. Поэтому адсорбционные силы значительны, и действуют на больших расстояниях по сравнению с межмолекулярными силами
уменьшается, и межмолекулярное взаимодействие увеличивается. Поэтому адсорбционные силы значительны, и действуют на больших расстояниях по сравнению с межмолекулярными силами 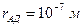 .
.
Энергия притяжения пир адсорбции зависит от расстояния в третьей степени вместо шестой, как это имеет место при взаимодействии двух атомов. Такая зависимость указывает на более медленное уменьшение энергии притяжения при адсорбции и на дальнодействие адсорбционых сил. Полная потенциальная энергия взаимодействия при адсорбции выражается уравнением
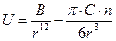 ,
,
где n - число атомов в единице объема адсорбента. Важными практическим выводом при рассмотрении природы адсорбционных сил является вывод о том, что, когда преобладают дисперсионные силы, наблюдается лучшая адсорбция в трещинах и порах, т.к. вблизи адсорбированной молекулы находится большое число атомов твердого тела. Если преобладают электростатические силы, то в трещинах и порах заряды компенсируют друг друга, и наибольший потенциал оказывается на выступах, где и будет преобладать адсорбция, особенно при образовании водородных связей.
Изотермы адсорбции
Вид изотермы адсорбции изображен на рис. 3.10.
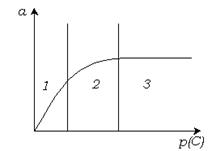
Рис. 3.10. Изотерма адсорбции 1 типа.
На кривой имеется три участка, расположенных в области низких, средних и высоких давлений. При малых 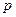 наблюдается линейна зависимость, т. к. поверхность адсорбента свободна, идет активное заполнение поверхности. В этой области адсорбция прямо пропорциональна давлению в соответствии с законом Генри:
наблюдается линейна зависимость, т. к. поверхность адсорбента свободна, идет активное заполнение поверхности. В этой области адсорбция прямо пропорциональна давлению в соответствии с законом Генри: 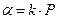 . Уравнение Генри можно получить путем рассмотрения адсорбции из газовой фазы на основе кинетического подхода.
. Уравнение Генри можно получить путем рассмотрения адсорбции из газовой фазы на основе кинетического подхода.
Рассмотрим динамическую картину адсорбционного процесса, поведение молекул в поверхностном слое, т.е. кинетику адсорбции.
Кинетические закономерности адсорбции определяют скорость установления равновесия при адсорбции, или сокращенно, скорость адсорбции. При столкновении с поверхностью молекула либо отражается от поверхности под углом, равном углу падения, либо некоторое время остается на поверхности, затем десорбируется. Чем больше времени молекула находится на поверхности, тем длительнее устанавливается равновесие. иными словами, скорость установления равновесия V увеличивается с уменьшением времени пребывания молекулы на поверхности t.
Величина адсорбции 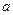 равна произведению времени пребывания молекулы на поверхности
равна произведению времени пребывания молекулы на поверхности 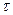 на число молекул, контактирующих с поверхностью в единицу времени. В этом и состоит динамическое уравнение адсорбции, которое записывается следующим образом:
на число молекул, контактирующих с поверхностью в единицу времени. В этом и состоит динамическое уравнение адсорбции, которое записывается следующим образом:
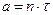
Из кинетической теории следует, что 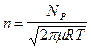
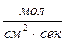 . При относительной влажности 10%
. При относительной влажности 10% 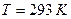 ,
, 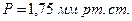 , число молекул воды, сталкивающихся с поверхностью в секунду равно 10.
, число молекул воды, сталкивающихся с поверхностью в секунду равно 10.
Площадь занимаемой молекулой воды на поверхности равна 10 Å2 , т. е. 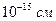 , следовательно
, следовательно 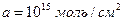 . Это означает, что
. Это означает, что 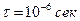 , а скорость установления равновесия крайне велика, монослой образуется практически мгновенно. А за время пребывания на поверхности молекулы адсорбата обмениваются тепловой энергией с поверхностью адсорбента. Таким образом, без адсорбции теплообмен был бы невозможен. Роль адсорбции в теплообмене составляет одно из важнейших ее проявлений в технических и природных процессах.
, а скорость установления равновесия крайне велика, монослой образуется практически мгновенно. А за время пребывания на поверхности молекулы адсорбата обмениваются тепловой энергией с поверхностью адсорбента. Таким образом, без адсорбции теплообмен был бы невозможен. Роль адсорбции в теплообмене составляет одно из важнейших ее проявлений в технических и природных процессах.
Я.И.Френкель в 1924 году получил выражение для зависимости 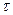 от
от 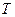 .
.
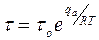
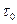 - константа, равная периоду колебаний в решетке адсорбента порядка
- константа, равная периоду колебаний в решетке адсорбента порядка 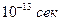 . Как видно из уравнения,
. Как видно из уравнения, 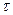 сильно зависит от
сильно зависит от 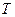 и
и 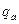 , т. к. они стоят в показателе степени.
, т. к. они стоят в показателе степени.
Ниже приведены значения 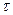 , вычисленные для различных
, вычисленные для различных 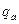 при комнатной температуре.
при комнатной температуре.
| Физическая адсорбция | Хемосорбция | ||
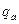 , кДж/моль , кДж/моль
| 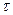 , с , с
| 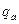 , кДж/моль , кДж/моль
| 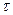 , с , с
|
| 1,6 | 1,1×10-12 1,3×10-12 1×10-10 3×10-6 | 2×10-2 1×102 6×105 4×109 1017 10126 |
Последнее значение 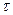 , больше возраста Земли и Солнечной системы.При
, больше возраста Земли и Солнечной системы.При 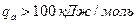 молекула живет на месте недели, годы или тысячелетия, поэтому хемосорбция в большинстве случаев является локализованной.
молекула живет на месте недели, годы или тысячелетия, поэтому хемосорбция в большинстве случаев является локализованной.
При адсорбции газов на гладкой поверхности равновесие устанавливается очень быстро, в течение долей секунды. При адсорбции на твердой пористой поверхности адсорбция замедляется вследствие проникновения адсорбата в поры адсорбента, контролируемого диффузией.
Объединяя уравнения (), () и (), получим закон Генри:
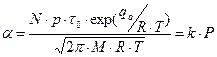
Участок 2, соответствующий средним давлениям является криволинейным, т.к. на этом участке достигается промежуточная степень заполнения поверхности адсорбента.
Изотерма адсорбции имеет вид параболы и описывается эмпирическим уравнением Фрейндлиха: 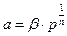 , где b и
, где b и 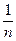 - константы, не имеющие физического смысла, но имеющие математический смысл. Эти константы не зависят от концентрации адсорбата. Это уравнение хорошо описывает среднюю часть изотермы. На начальном, линейном участке изотермы
- константы, не имеющие физического смысла, но имеющие математический смысл. Эти константы не зависят от концентрации адсорбата. Это уравнение хорошо описывает среднюю часть изотермы. На начальном, линейном участке изотермы 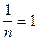 , и а пропорциональна
, и а пропорциональна 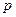 . На третьем участке
. На третьем участке 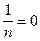 и
и 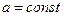 . Следовательно, показатель степени
. Следовательно, показатель степени 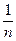 характеризует кривизну криволинейного участка изотермы адсорбции. Это правильная дробь, характеризующая степень приближения изотермы к прямой. Чем больше значение
характеризует кривизну криволинейного участка изотермы адсорбции. Это правильная дробь, характеризующая степень приближения изотермы к прямой. Чем больше значение 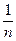 , тем круче криволинейный участок изотермы адсорбции. Для решения уравнения Фрейндлиха применяют логарифмирование. После логарифимирования уравнение принимает вид
, тем круче криволинейный участок изотермы адсорбции. Для решения уравнения Фрейндлиха применяют логарифмирование. После логарифимирования уравнение принимает вид 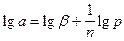 . Из графической зависимости находят константы b и
. Из графической зависимости находят константы b и 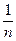 . Отрезок, отсекаемый прямой линией на оси ординат, равен
. Отрезок, отсекаемый прямой линией на оси ординат, равен 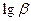 , а
, а 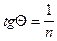 (рис. 3.11)
(рис. 3.11)
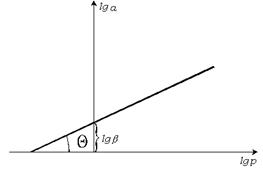
Рис. 3.11. Решение уравнения Фрейндлиха.
Я.Б.Зельдович показал, что при экспоненциальном распределении неоднородностей поверхности и среднем заполнении уравнение Фрейндлиха может быть получено теоретически.
Существует 5 основных типов изотерм адсорбции (рис. 3.12)
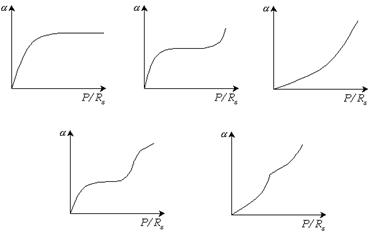
Рис. 3.12. Изотермы физической адсорбции.
Изотерма адсорбции 1 типа описывается уравнением Ленгмюра:
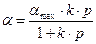
Этот тип изотермы соответствует мономолекулярной адсорбции. Остальные типы изотерм соответствуют полимолекулярной адсорбции: 2 – S-образная кривая с линейным участком в области средних давлений; 3 – кривая, вогнутая к оси адсорбции без перегибов с монотонным увеличением 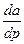 ; 4, 5 – кривые типов 2, 3, осложненные капиллярной конденсацией, сопровождающей полимолекулярную адсорбцию.
; 4, 5 – кривые типов 2, 3, осложненные капиллярной конденсацией, сопровождающей полимолекулярную адсорбцию.
Кинетика адсорбции
Кинетика адсорбции подчиняется уравнению первого порядка. Чем больше насыщение поверхности, т. е. меньше разность ( 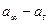 ), тем меньше скорость адсорбции.
), тем меньше скорость адсорбции.
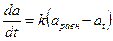
С повышением температуры скорость адсорбции увеличивается, а равновесная адсорбция уменьшается (рис. 3.13).
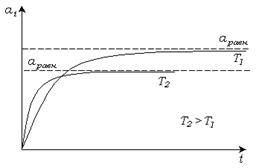
Рис. 3. 13. Кинетика адсорбции.
Константа 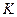 зависит от теплоты адсорбции, температуры и коэффициента диффузии адсорбата. Температурный коэффициент адсорбции мал, т. к. энергия активации физической адсорбции равна 0.
зависит от теплоты адсорбции, температуры и коэффициента диффузии адсорбата. Температурный коэффициент адсорбции мал, т. к. энергия активации физической адсорбции равна 0.
Дата добавления: 2020-11-18; просмотров: 1235;











