Согласованная фильтрация радиоимпульсов
В случае полосовых сигналов цифровой модуляции (АФМ-М, ФМ-М, КАМ-M и др.) канальные символы строятся на основе импульса-переносчика
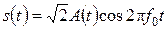 . (8.1)
. (8.1)
Сигнал s(t) является полосовым. Его спектр сосредоточен вокруг частоты f0. Необходимо выполнить оптимальную фильтрацию сигнала s(t), поступающего вместе с помехой n(t), и взять отсчет. Считаем, что помеха – белый шум, его спектр сосредоточен в полосе пропускания канала связи.
Первый способ выполнения СФ – использовать полосовой фильтр, АЧХ которого описывается соотношением (4.13). Инженерная практика показала, что полосовые фильтры имеют невысокую точность реализации.
Второй способ состоит в следующем: сначала выполняется когерентное (синхронное) детектирование суммы сигнала и помехи z(t) = s(t) + n(t), а затем – фильтрация импульса A(t) с помехой низкочастотным согласованным фильтром (рис. 8.1). Схема восстановления несущего колебания (ВН) вырабатывает колебание 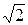 cos 2pf0t, необходимое для работы детектора.
cos 2pf0t, необходимое для работы детектора.
Для анализа прохождения шума через синхронный детектор полосовой шум представим квадратурными составляющими
n(t) = 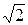 Nc(t)cos 2pf0t +
Nc(t)cos 2pf0t + 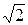 Ns(t)sin 2pf0t, (8.2)
Ns(t)sin 2pf0t, (8.2)
где 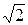 Nc(t) – амплитуда косинусной составляющей помехи;
Nc(t) – амплитуда косинусной составляющей помехи;
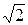 Ns(t) – амплитуда синусной составляющей помехи.
Ns(t) – амплитуда синусной составляющей помехи.
 |
На выходе перемножителя получим
uпер(t) = [А(t) + Nc(t)] + [А(t) + Nc(t)]cos 2p2f0t. (8.3)
Первое слагаемое в выражении (8.3) – низкочастотная составляющая, а второе слагаемое – сигнал балансной модуляции с частотой несущего колебания 2f0. В системах передачи частота несущего колебания существенно больше максимальной частоты спектра сигнала А(t), и спектры двух слагаемых в (8.3) не перекрываются. Для получения сигнала А(t) после перемножителя необходимо включить ФНЧ, пропускающий А(t) и ослабляющий А(t) cos 2p2f0t. Т.е., требуется фильтр с частотой среза большей, чем максимальная частота в спектре сигнала А(t). Роль этого фильтра будет выполнять СФ, выполняющий оптимальную фильтрацию сигнала А(t). На выходе СФ за счет импульса А(t) получим импульс P(t) (раздел 5).
Обсудим прохождение шума через синхронный детектор и согласованный фильтр. Шум n(t) белый в полосе пропускания канала связи Fк со средней частотой f0. Средняя мощность шума определяется Pn = N0Fк. Эта мощность делится поровну между косинусной и синусной составляющими. Так, мощность косинусной составляющей
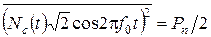 . (8.4)
. (8.4)
Выполнив усреднение левой части равенства (8.4), получим
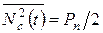 . (8.5)
. (8.5)
Шум Nc(t) является белым в полосе частот (0, Fк/2). Его удельная мощность равна
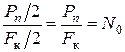 . (8.6)
. (8.6)
Из анализа преобразований сигнала и помехи синхронным детектором видно, что на входе фильтра, согласованного с А(t), действует сигнал А(t) и белый шум с удельной мощностью N0. Эта фильтрация рассмотрена в разделе 5. СФ обеспечивает отношение мгновенной мощности сигнала к средней мощности шума
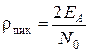 . (8.7)
. (8.7)
Определим энергию сигнала s(t)
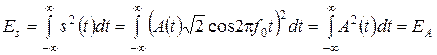 . (8.8)
. (8.8)
Таким образом, схема, приведенная на рис. 8.1, обеспечивает отношение сигнал/шум
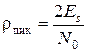 , (8.9)
, (8.9)
т.е. является фильтром, согласованным с полосовым сигналом s(t).
Именно такая схема согласованной фильтрации полосовых сигналов используется в демодуляторах двумерных сигналов цифровой модуляции для оптимальной фильтрации сигналов. При использовании двух таких схем с опорными колебаниями cos 2pf0t и sin 2pf0t происходит разделение косинусного и синусного радиоимпульсов и их следующая раздельная обработка.
Контрольные вопросы
1. Опишите два способа согласованной фильтрации радиоимпульсов.
2. Объясните назначение схемы восстановления несущего колебания.
9. Оптимальные демодуляторы одномерных
полосовых сигналов
Рассмотрим одномерные сигналы. Это сигналы АМ-M и ФМ-2. Канальные символы описываются
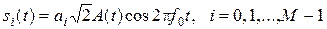 , (9.1)
, (9.1)
где 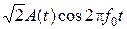 – радиоимпульс с определенными временными и спектральными характеристиками, максимальное значение и энергия которого равны 1;
– радиоимпульс с определенными временными и спектральными характеристиками, максимальное значение и энергия которого равны 1;
аі – коэффициенты, отображающие n = log2M переданных бит согласно модуляционному коду.
Выше было найдено, что основными элементами оптимального демодулятора являются: согласованный фильтр, дискретизатор и схема решения. Выше было сказано, что оптимальную фильтрацию радиоимпульсов следует выполнять схемой, которая содержит синхронный детектор и низкочастотный согласованный фильтр. Для работы синхронного детектора необходимое колебание 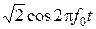 , вырабатываемое схемой восстановления несущего колебания (ВН). Работой дискретизатора управляют импульсы, поступающие от схемы тактовой синхронизации (ТС). Поэтому схема демодулятора имеет вид, показанный на рис. 9.1.
, вырабатываемое схемой восстановления несущего колебания (ВН). Работой дискретизатора управляют импульсы, поступающие от схемы тактовой синхронизации (ТС). Поэтому схема демодулятора имеет вид, показанный на рис. 9.1.
 |
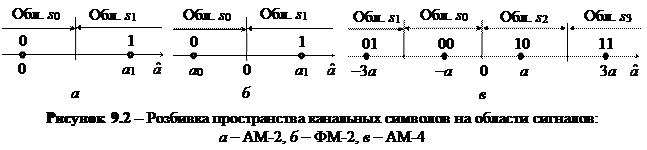
Правило вынесения решения формулируется на основе разбивки пространства канальных символов на М непересекающихся областей si, i = 0, …, М – 1; каждая область si – это совокупность точек, которые ближе к сигналу si(t), чем к другим сигналам. Схема решений выдает решение битами согласно модуляционному коду.
Контрольные вопросы
1. Объясните назначение отдельных блоков оптимального демодулятора сигналов АМ-M и ФМ-2.
2. Сформулируйте правило вынесения решения на основе разбивки пространства канальных символов на М областей.
10. Оптимальные демодуляторы двумерных
полосовых сигналов
В случае двумерных сигналов ФМ-M (M ³ 4), АФМ-M, КАМ-M канальные символы описываются
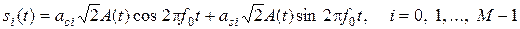 , (10.1)
, (10.1)
где асі и аsі – пары коэффициенты, которые отображают n = log2M передаваемых бит согласно модуляционному коду.
Канальные символы состоят из косинусных и синусных импульсов. Их необходимо разделить. Это осуществляется с помощью двух синхронных детекторов, которые отличаются опорными колебаниями – если опорное колебание 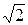 cos2pf0t, то детектор не реагирует на синусную составляющую входного сигнала, если опорное колебание
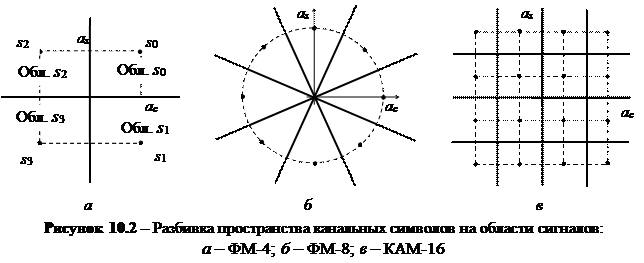
cos2pf0t, то детектор не реагирует на синусную составляющую входного сигнала, если опорное колебание 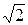 sin 2pf0t, то детектор не реагирует на косинусную составляющую входного сигнала. Поэтому с помощью двух детекторов осуществляется разделение косинусного и синусного импульсов и последующая их раздельная обработка в двух подканалах демодулятора (рис. 10.1): согласованная фильтрация и дискретизация. Оценки коэффициентов
sin 2pf0t, то детектор не реагирует на косинусную составляющую входного сигнала. Поэтому с помощью двух детекторов осуществляется разделение косинусного и синусного импульсов и последующая их раздельная обработка в двух подканалах демодулятора (рис. 10.1): согласованная фильтрация и дискретизация. Оценки коэффициентов 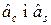 поступают на схему решения.
поступают на схему решения.
Как и в случае одномерных сигналов, правило вынесения решений формулируется на основе разбивки пространства сигналов на М непересекающихся областей si, i = 0, …, М – 1; каждая область si – это совокупность точек, которые ближе к сигналу si(t), чем к другим сигналам. Отличие заключается в том, что пространство сигналов двумерное. Если точка ( 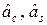 ) попала в область сигнала si, то выносится решение о том, что передавался сигнал si. Схема решения выдает решение битами согласно модуляционному коду.
) попала в область сигнала si, то выносится решение о том, что передавался сигнал si. Схема решения выдает решение битами согласно модуляционному коду.
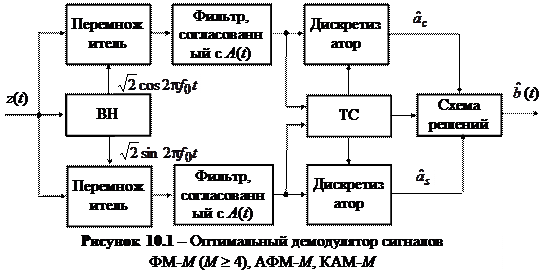
На рис. 10.2 показанная разбивка пространств канальных символов на области сигналов. Границы областей показаны жирными линиями. В случае сигнала ФМ-4 области сигналов – 4 квадранта; в случае сигнала ФМ-8 области сигналов – 8 секторов; в случае сигнала КАМ-16 области сигналов образованы вертикальными и горизонтальными прямыми. Благодаря простоте разбивки пространства двумерных сигналов КАМ-М на области сигналов они получили самое широкое распространение среди сигналов АФМ-М.
 |
К двумерным сигналам относятся также сигналы ЧМ-2. Канальные символы описываются
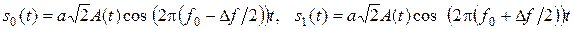 , (10.2)
, (10.2)
где Df – разнос частот.
Если разнос частот удовлетворяет условию Df = k/(2Т), где k = 1, 2, …, то сигналы ортогональные, и они могут быть разделены синхронными детекторами (аналогично разделению косинусного и синусного импульсов). Схема оптимального демодулятора сигнала ЧМ-2 подобна схеме, приведенной на рис. 10.1, но отличается опорными колебаниями в синхронных детекторах (рис. 10.3).
 | |||
 |

На рис. 10.4 показанная разбивка пространства канальных символов ЧМ-2 на области сигналов. Граница областей показана жирной линией. Из этого рисунку видно, что для вынесения решения о переданном сигнале достаточно сравнить оценки амплитуд сигналов s0(t) и s1(t): если 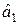 >
> 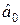 , то выносится решение
, то выносится решение 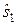 и наоборот.
и наоборот.
Контрольные вопросы
1. Объясните назначение отдельных блоков оптимального демодулятора двумерных сигналов КАМ-M и ФМ-М.
2. Сформулируйте правило вынесения решения на основе разбивки пространства канальных символов на М областей.
11. Вероятность ошибки при оптимальной демодуляции
одномерных сигналов цифровой модуляции
Как отмечалось в разд. 2, критерием оптимальности демодулятора является минимум полной вероятности ошибки решения относительно канального символа Рош. Но для пользователей количественной мерой помехоустойчивости цифровой системы передачи является вероятность ошибки бита р. В двоичных системах передачи вероятности Рош и р совпадают. В случае многоуровневых видов модуляции сначала находят Рош, затем рассчитывают р, зная модуляционный код.
В.А. Котельников ввел термин «потенциальная помехоустойчивость приема» – это максимальная помехоустойчивость, которую обеспечивает оптимальный демодулятор. В сущности, это помехоустойчивость используемого модулированного сигнала при заданных характеристиках канала связи.
Анализ вероятности ошибки начнем из рассмотрения одномерных двоичных сигналов. Воспользуемся результатами, полученными в разд. 2. На рис. 2.1, б для одномерного двоичного сигнала показаны сигнальное созвездие и условные плотности вероятности оценки 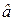 . Было сформулировано правило вынесения решения по результатам сравнения оценки
. Было сформулировано правило вынесения решения по результатам сравнения оценки 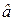 с граничным значением l: если
с граничным значением l: если 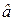 > l, то передавался символ s1(t), а если
> l, то передавался символ s1(t), а если 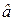 < l, то передавался символ s0(t). Оптимальное значение l находится посредине между а1 и а0:
< l, то передавался символ s0(t). Оптимальное значение l находится посредине между а1 и а0:
l = 0,5(а1 + а0). (11.1)
При этом вероятности ошибок при передаче сигналов s0(t) и s1(t) одинаковы и определяются выражением
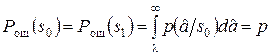 . (11.2)
. (11.2)
Условная плотность вероятности 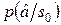 имеет нормальное распределение вероятностей со средним значением равным a0. С учетом этого (11.2) запишется
имеет нормальное распределение вероятностей со средним значением равным a0. С учетом этого (11.2) запишется
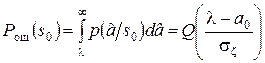 , (11.3)
, (11.3)
где sz – СКО шума на выходе согласованного фильтра, определенное раньше соотношением (5.14).
Примем в рассмотрение расстояние между сигналами
d = (а1 – а0). (11.4)
Из соотношений (11.1) и (11.4) получим
l = а0 + 0,5d (11.5)
С учетом (5.14) и (11.5) соотношение (11.3) дает вероятность ошибки канального символа в двоичной системе передачи
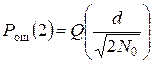 . (11.6)
. (11.6)
Из определения гауссовой Q-функции 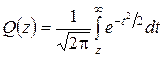 вытекает, что, чем большее значение аргумента, тем меньшее значение функции Q(z). Вероятность ошибки канального символа (11.6) будет уменьшаться при увеличении расстояния между сигналами d и уменьшении удельной мощности шума N0 на входе демодулятора.
вытекает, что, чем большее значение аргумента, тем меньшее значение функции Q(z). Вероятность ошибки канального символа (11.6) будет уменьшаться при увеличении расстояния между сигналами d и уменьшении удельной мощности шума N0 на входе демодулятора.
Дальше задача заключается в том, чтобы выразить расстояние между сигналами в (11.6) через физические параметры сигнала, действующего на входе демодулятора. Такими параметрами являются: средняя мощность модулированного сигнала Ps и скорость цифрового сигнала R или обратная к ней величина – длительность двоичного символа Тб = 1/R.
 Упражнение 11.1. Найдем вероятность ошибки для одномерных двоичных сигналов ФМ-2 и АИМ-2. На рис. 11.1 приведены сигнальные созвездия сигналов ФМ-2 и АИМ-2. Поскольку базисная функция нормирована, то выполняется равенство (5.12), и Еб = а2. Отсюда d = 2а = 2
Упражнение 11.1. Найдем вероятность ошибки для одномерных двоичных сигналов ФМ-2 и АИМ-2. На рис. 11.1 приведены сигнальные созвездия сигналов ФМ-2 и АИМ-2. Поскольку базисная функция нормирована, то выполняется равенство (5.12), и Еб = а2. Отсюда d = 2а = 2 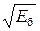 . Вероятность ошибки бита определяется
. Вероятность ошибки бита определяется
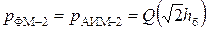 , (11.7)
, (11.7)
где  – отношение сигнал/шум.
– отношение сигнал/шум.
 Упражнение 11.2. Найдем вероятность ошибки для двоичного сигнала АМ-2. На рис. 11.2 приведено сигнальное созвездие сигнала АМ-2. Поскольку базисная функция нормирована, то выполняется равенство (5.12), и Е1 = а2, а Е0 = 0. Еб = 0,5(Е1 + Е0) = 0,5а2. Отсюда d = а =
Упражнение 11.2. Найдем вероятность ошибки для двоичного сигнала АМ-2. На рис. 11.2 приведено сигнальное созвездие сигнала АМ-2. Поскольку базисная функция нормирована, то выполняется равенство (5.12), и Е1 = а2, а Е0 = 0. Еб = 0,5(Е1 + Е0) = 0,5а2. Отсюда d = а = 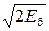 .
.
Вероятность ошибки бита определяется
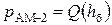 . (11.8)
. (11.8)
Перейдем к многопозиционным системам передачи, т.е. М > 2. Если канальные символы равновероятны, то вероятность ошибки канального символа определяется
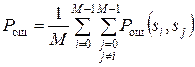 . (11.9)
. (11.9)
где Pош(si, sj) – вероятность ошибки в двоичной системе, использующей сигналы si и sj, а ошибка состоит в вынесении решения о передаче 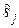 , если было передано si. Чтобы упростить расчеты, учитывают переходы лишь в ближайшие сигналы (это допустимо при высоких отношениях сигнал/шум, которые соответствуют вероятности ошибки Рош < 10–2). Переход от ошибки канального символа Рош к ошибке двоичного символа р выполняется легко, если используется модуляционный код Грея:
, если было передано si. Чтобы упростить расчеты, учитывают переходы лишь в ближайшие сигналы (это допустимо при высоких отношениях сигнал/шум, которые соответствуют вероятности ошибки Рош < 10–2). Переход от ошибки канального символа Рош к ошибке двоичного символа р выполняется легко, если используется модуляционный код Грея:
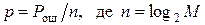 . (11.10)
. (11.10)
 Упражнение 11.3. Найдем вероятность ошибки для многопозиционных одномерных сигналов АМ-М и АИМ-М. На рис. 11.3 приведены сигнальные созвездия сигналов АМ-4 и АИМ-4. Аналогично строятся созвездия при М > 4. Задачу будем решать для произвольного М (М – целая степень числа 2).
Упражнение 11.3. Найдем вероятность ошибки для многопозиционных одномерных сигналов АМ-М и АИМ-М. На рис. 11.3 приведены сигнальные созвездия сигналов АМ-4 и АИМ-4. Аналогично строятся созвездия при М > 4. Задачу будем решать для произвольного М (М – целая степень числа 2).
Коэффициенты аі принимают значение 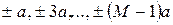 . Определим среднюю энергию канального символа
. Определим среднюю энергию канального символа
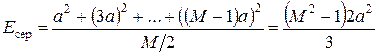 . (11.11)
. (11.11)
Учтем, что
d = 2a и 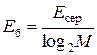 . (11.12)
. (11.12)
На основе (11.11) и (11.12) получим выражение для квадрата расстояния
 . (11.13)
. (11.13)
При анализе вероятности ошибки достаточно учесть переходы лишь в ближайшие канальные символы, поэтому
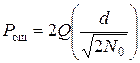 . (11.14)
. (11.14)
Учитывая (11.10), (11.13) и (11.14) получим выражение вероятности ошибки двоичного символа
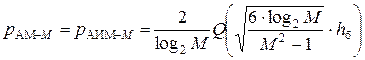 . (11.15)
. (11.15)
Контрольные вопросы
1. Запишите и объясните формулу вероятности ошибки канального символа в двоичной системе передачи.
2. Объясните, что представляет собой величина 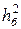 .
.
3. Объясните, какие упрощения допускают при анализе помехоустойчивости многопозиционных сигналов.
12. Вероятность ошибки при оптимальной демодуляции
двумерных сигналов цифровой модуляции
При анализе помехоустойчивости двумерных сигналов может возникнуть одна из двух ситуаций.
1. Линия, которая соединяет сигналы si и sj, входящие в формулу (11.9), совпадает с одной из осей координат пространства сигналов. В этом случае вероятность ошибки в двоичной системе, использующей сигналы si и sj, определяется формулой (11.6), как и в случае одномерных сигналов.
2. Линия, которая соединяет сигналы si и sj, входящие в формулу (11.9), не совпадает ни с одной из осей координат пространства сигналов (рис. 12.1). На этом рисунке показаны шумовые компоненты оценок: 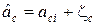 и
и 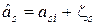 , где zс и zs – гауссовские независимые величины с нулевым средним и СКО
, где zс и zs – гауссовские независимые величины с нулевым средним и СКО 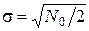 – формула (5.14). На основе рис. 12.1 условие возникновения ошибки – вынесение решения о передаче
– формула (5.14). На основе рис. 12.1 условие возникновения ошибки – вынесение решения о передаче 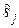 , если было передано si
, если было передано si
 Pош(si, sj) = Р {h > d/2}, (12.1)
Pош(si, sj) = Р {h > d/2}, (12.1)
где h = zс cos a +zs cos (90°– a) гауссовская случайная величина. Ее дисперсия
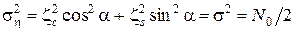 . (12.2)
. (12.2)
Таким образом, и в случае ситуации 2 вероятность ошибки (12.1) определяется формулой (11.6), как и в случае одномерных сигналов.
Упражнение 12.1. Найдем вероятность ошибки для многопозиционного двумерного сигнала ФМ-4 (рис. 12.2): координаты канальных символов ±а, а расстояния между ближайшими символами d = 2a. Энергии канальных символов одинаковые 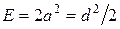 . Энергия сигнала на бит
. Энергия сигнала на бит

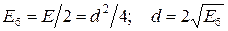 . (12.3)
. (12.3)
Из рис. 12.2 видно, что достаточно учесть переходы лишь в два ближайших канальных символа, поэтому, учитывая формулу (11.6)
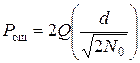 . (12.4)
. (12.4)
Учитывая формулы (11.10) и (12.4), получим выражение для вероятности ошибки двоичного символа при ФМ-4
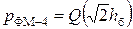 . (12.5)
. (12.5)
 Упражнение 12.2. Найдем вероятность ошибки для многопозиционного сигнала ФМ-М. Точки сигнального созвездия находятся на окружности радиуса а с угловым шагом 2p/М. Ясно, что достаточно учесть переходы лишь в два ближайших канальных символа. На рис.12.3 приведен фрагмент сигнального созвездия сигнала ФМ-М. Выразим расстояние между ближайшими точками через радиус окружности. Поскольку d/2 = a×sin(p/M), то d = 2a sin(p/M). Энергии канальных символов одинаковые: Е = а2. Энергия сигнала на бит определяется
Упражнение 12.2. Найдем вероятность ошибки для многопозиционного сигнала ФМ-М. Точки сигнального созвездия находятся на окружности радиуса а с угловым шагом 2p/М. Ясно, что достаточно учесть переходы лишь в два ближайших канальных символа. На рис.12.3 приведен фрагмент сигнального созвездия сигнала ФМ-М. Выразим расстояние между ближайшими точками через радиус окружности. Поскольку d/2 = a×sin(p/M), то d = 2a sin(p/M). Энергии канальных символов одинаковые: Е = а2. Энергия сигнала на бит определяется 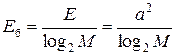 и расстояние
и расстояние 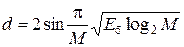 .
.
Используя формулы (11.10) и (12.4), получим выражение для вероятности ошибки двоичного символа при ФМ-М для М ³ 4
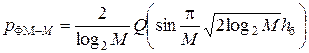 . (12.5)
. (12.5)
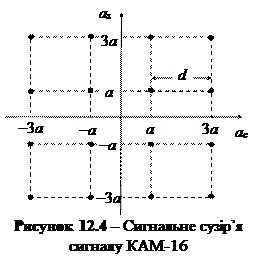 Упражнение 12.3. Найдем вероятность ошибки для многопозиционных двумерных сигналов КАМ-16 (рис. 12.4). Возьмем одну из четырех точек, которые размещены возле начала координат. Для любой из них видно, что достаточно учесть переходы лишь в четыре ближайших канальных символа, поэтому, учитывая формулу (11.6)
Упражнение 12.3. Найдем вероятность ошибки для многопозиционных двумерных сигналов КАМ-16 (рис. 12.4). Возьмем одну из четырех точек, которые размещены возле начала координат. Для любой из них видно, что достаточно учесть переходы лишь в четыре ближайших канальных символа, поэтому, учитывая формулу (11.6)
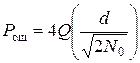 . (12.6)
. (12.6)
Найдем среднюю энергию канального символа
Еср = (4×2а2 + 8×10а2 + 4×18а2)/16 = 10а2. (12.7)
Энергия сигнала на бит определяется 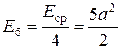 и расстояние
и расстояние 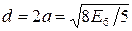 .
.
Используя формулы (11.10) и (12.6), получим выражение для вероятности ошибки двоичного символа при КАМ-16
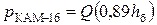 . (12.8)
. (12.8)
Можно получить общую формулу вероятности ошибки бита для сигналов КАМ-М (М ³ 16) при условии, что log2M является четным числом
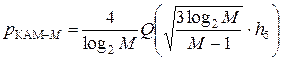 . (12.9)
. (12.9)
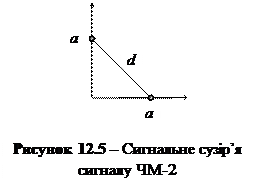 Упражнение 12.4. Найдем вероятность ошибки для двоичного сигнала ЧМ-2 (рис. 12.5): координаты канальных символов равны а, а расстояние между символами d =
Упражнение 12.4. Найдем вероятность ошибки для двоичного сигнала ЧМ-2 (рис. 12.5): координаты канальных символов равны а, а расстояние между символами d = 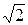 a. Энергии канальных символов одинаковые
a. Энергии канальных символов одинаковые 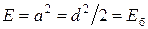 .
.
По формуле (11.6) получим
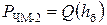 . (12.10)
. (12.10)
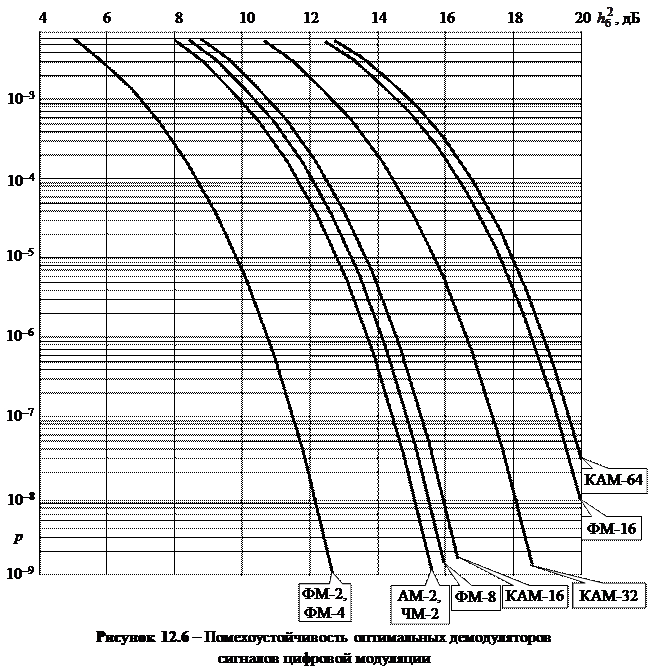
Полученные в разд. 11 и 12 формулы позволяют определить вероятности ошибки бита р при заданном отношении сигнал/шум 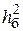 или необходимое отношение сигнал/шум при заданной вероятности ошибки бита. Анализ помехоустойчивости удобно проводить, используя графики зависимости р = f (
или необходимое отношение сигнал/шум при заданной вероятности ошибки бита. Анализ помехоустойчивости удобно проводить, используя графики зависимости р = f ( 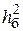 ) (рис. 12.6). При построении графика отношение сигнал/шум принято выражать в децибелах и использовать для него линейный масштаб. Для вероятности ошибки используют логарифмический масштаб.
) (рис. 12.6). При построении графика отношение сигнал/шум принято выражать в децибелах и использовать для него линейный масштаб. Для вероятности ошибки используют логарифмический масштаб.
Из приведенных на рис. 12.6 данных вытекает, что наивысшая помехоустойчивость свойственна сигналам ФМ-2 и ФМ-4.
Контрольные вопросы
1. Запишите и поясните формулы вероятности ошибки двоичного символа сигналов ФМ-4, ФМ-8, КАМ-16. Сравните помехоустойчивость.
2. Объясните, почему с ростом числа позиций сигнала ухудшается помехоустойчивость.
Дата добавления: 2016-07-27; просмотров: 2906;











