Согласованный фильтр при небелом шуме
Есть сумма сигнала и помехи z(t) = s(t) + n(t). Сигнал s(t) детерминированный, помеха n(t) характеризуется спектральной плотностью мощности Gn(w), –¥ < w < ¥, которая не является постоянной величиной. Необходимо найти передаточную функцию фильтра H(jw), согласованного с сигналом s(t), т.е. фильтр, который обеспечивает максимальное отношение сигнал/помеха в отсчетный момент.
Из разд. 4 известна передаточная функция согласованного фильтра при белом шуме:
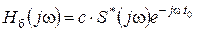 . (7.1)
. (7.1)
Воспользуемся этим результатом. Пропустим сигнал z(t) через обеляющий фильтр с передаточной функцией H1(jw). Найдем АЧХ обеляющего фильтра, который преобразует помеху с неравномерным спектром в белый шум:
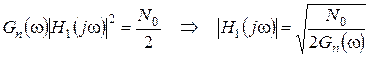 , (7.2)
, (7.2)
где N0/2 – удельная мощность белого шума.
Пусть S(jw) – спектральная плотность сигнала s(t). После обеляющего фильтра спектральная плотность полезного сигнала s1(t) определяется S(jw)H1(jw). На основе соотношения (7.1) запишем передаточную функцию фильтра, согласованного с сигналом s1(t)
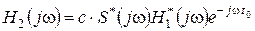 . (7.3)
. (7.3)
Каскадно соединенные обеляющий фильтр и фильтр, согласованный с сигналом s1(t), образуют согласованный фильтр при небелом шуме с передаточной функцией
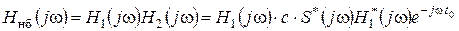 . (7.4)
. (7.4)
После подстановки выражения для ïH(jw)ï2 с соотношение (7.2) получим (множитель N0/2 отнесем к произвольному коэффициенту с):
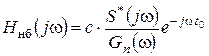 . (7.5)
. (7.5)
Из полученного выражения следует, что значение АЧХ СФ при небелом шуме в сравнении со значениями АЧХ СФ при белом шуме меньше на тех частотах, на которых удельная мощность помехи больше. Требования к ФЧХ СФ при небелом шуме такие же, как и требования к ФЧХ СФ при белом шуме.
Отметим, что реализация СФ при небелом шуме не требует использования обеляющего фильтра. Обеляющий фильтр необходим для выполнения выкладок (7.2) – (7.5).
Контрольные вопросы
1. Что такое обеляющий фильтр?
2. Запишите и объясните формулу АЧХ обеляющего фильтра.
Дата добавления: 2016-07-27; просмотров: 2265;











