Системы восстановления несущего колебания
Система восстановления несущего колебания (ВН) демодуляторов полосовых сигналов цифровой модуляции предназначена для формирования опорного гармонического колебания, фаза которого совпадает с фазой несущей, на основе которой сформирован демодулируемый сигнал.
Уже в 30-е годы прошлого столетия стало ясно, что сигналы ФМ-2 имеют наивысшую помехоустойчивость. Для применения этих сигналов в системах передачи необходимо было решить задачу восстановления несущего (опорного) колебания в демодуляторе, которое необходимое для работы синхронного детектора. В те годы была предложена схема восстановления несущего колебания с умножением частоты на 2 (рис. 13.1).
 |
В случае ФМ-2 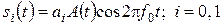 . Коэффициенты ai заданы сигнальным созвездием (рис. 11.1). Канальные символы:
. Коэффициенты ai заданы сигнальным созвездием (рис. 11.1). Канальные символы:
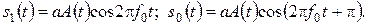 (13.1)
(13.1)
Много десятилетий использовались «слабо» фильтрованные импульсы A(t), которые были близки по форме к П-импульсу на интервале длительностью Т
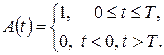 (13.2)
(13.2)
После умножения частоты на 2, как сигнал s1(t), так и сигнал s0(t) дают  . Узкополосный фильтр имеет среднюю частоту полосы пропускания 2f0. Он предназначен для ослабления помех. Делитель частоты на 2 может выдать одно из двух возможных опорных колебаний:
. Узкополосный фильтр имеет среднюю частоту полосы пропускания 2f0. Он предназначен для ослабления помех. Делитель частоты на 2 может выдать одно из двух возможных опорных колебаний:
- случай 1: 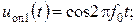
- случай 2: 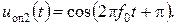
Оба колебания возможны, так как результат зависит от того, которые начальные условия сложатся в схеме делителя. Говорят, что опорное колебание имеет неопределенность фазы порядка 180°.
В случае 1 реализуется алгоритм оптимальной демодуляции сигнала
ФМ-2. В случае 2 на выходе перемножителя, а затем и согласованного фильтра, и дискретизатора будут напряжения, противоположные тем, которые имеют место в случае 1. Схема решения будет выносить инверсные решения: вместо 1 выдает 0 и наоборот. Такое явление получило название инверсная (обратная) робота демодулятора. Оказалось, что и в процессе работы демодулятора могут происходить случайные скачкообразные переходы от колебания uоп1(t) к колебанию uоп2(t) и наоборот.
В демодуляторе сигнала ФМ-4 необходимо использовать умножитель частоты на 4, фильтр со средней частотой полосы пропускания 4f0 и делитель частоты на 4. После делителя частоты возникает одно из опорных колебаний, которые отличаются по фазе с шагом 90°. Имеет место неопределенность фазы опорного колебания порядка 90°.
Устранить проявление неопределенности фазы опорного колебания в демодуляторе удается при использовании разностного (относительного) кодирования. Такие методы передачи получили название фазоразностной (относительной фазовой) модуляции.
Выше рассмотрена система ВН с возведением в степень. Однако она хорошо работает, когда амплитуда импульса A(t) близка к прямоугольной форме. Ныне используются импульсы Найквиста – импульсы с существенно сглаженной формой A(t). При такой форме импульса система ВН с возведением в степень работает плохо.
Опорное колебание необходимое для работы синхронного детектора (рис. 13.2). Пусть на вход детектора поступает сигнал ФМ-2. Канальный символ описывается
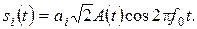 (13.3)
(13.3)
Если фаза колебания от генератора
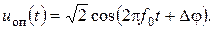 (13.4)
(13.4)
отличается от фазы несущей входного сигнала на величину Dj, то сигнал на выходе синхронного детектора получает множитель cosDj:
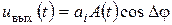 . (13.5)
. (13.5)
Поскольку максимальное значение косинуса равняется единице и достигается лишь в случае Dj = 0, наличие разности фаз приводит к уменьшению уровня сигнала на выходе детектора. Если же Dj = p/2, то сигнал на выходе детектора вообще отсутствует: 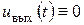 .
.
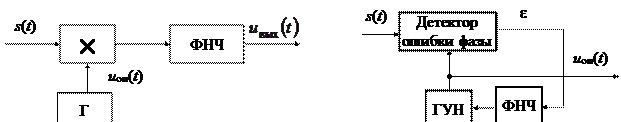 |
Ныне система ВН – это система фазовой автоматической подстройки частоты (ФАПЧ) (рис. 13.3) со специальным детектором ошибки фазы, которая способна работать в условиях отсутствия несущей в спектре сигнала. Здесь ГУН – генератор, управляемый напряжением. При появлении напряжения ошибки фазы e, этим напряжением подстраивается частота и фаза колебания, производимого ГУНом, так, чтобы уменьшить величину ошибки фазы.
Рассмотрим построение детектора ошибки фазы в случае сигнала ФМ-2. Схема детектора содержит еще один дополнительный синхронный детектор, опорным колебанием которого является 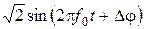 . Напомним, что работу синхронного детектора можно рассматривать как вычисление проекции s(t) на uоп(t). Два синхронных детекторы отличаются опорными колебаниями, сдвинутыми по фазе на 90°. Поэтому получаемые напряжения с выходов синхронных детекторов являются квадратурными составляющими детектируемого сигнала.
. Напомним, что работу синхронного детектора можно рассматривать как вычисление проекции s(t) на uоп(t). Два синхронных детекторы отличаются опорными колебаниями, сдвинутыми по фазе на 90°. Поэтому получаемые напряжения с выходов синхронных детекторов являются квадратурными составляющими детектируемого сигнала.
На рис. 13.4 показано сигнальное созвездие демодулируемого сигнала ФМ‑2 и вычисленные квадратурные составляющие в момент отсчета при условии, что демодулируется канальный символ с амплитудой а: I – синфазная составляющая, Q – квадратурная составляющая. На рис. 13.4, а ошибка фазы опорного колебания Dj = 0; при этом синхронные детекторы вычисляют I = а, Q = 0. На рис. 13.4, б ошибка фазы опорного колебания Dj > 0; при этом синхронные детекторы вычисляют I = а×cosDj, Q < 0. На рис. 13.4, в ошибка фазы опорного колебания Dj < 0; при этом синхронные детекторы вычисляют I = а×cosDj, Q > 0.
Видим, что знак значения Q соответствует ошибке фазы: а именно, если Q < 0, то Dj > 0 и необходимо уменьшать частоту и фазу ГУН, если же Q > 0, то Dj < 0 и необходимо увеличивать частоту и фазу ГУН. Таким образом, значение Q можно принять в качестве ошибки фазы e. Но ситуация со знаком Q противоположная при демодуляции канального символа с амплитудой –а.
Костас предложил в качестве ошибки фазы опорного колебания в демодуляторе сигнала ФМ-2 использовать
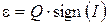 . (13.6)
. (13.6)
На рис. 13.5 показанная схема демодулятора сигнала ФМ-2 с раскрытой схемой восстановления несущего колебания.
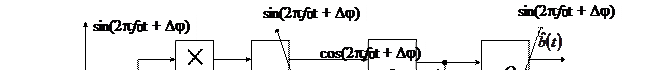
Для построения системы ВН демодулятора сигнала ФМ-4 используется детектор ошибки фазы, вычисляемой по алгоритму Костаса
 . (13.7)
. (13.7)
Здесь признаком ошибки фазы опорного колебания есть неравенство модулей квадратурных составляющих I и Q. Такой же алгоритм вычисления ошибки фазы используется и в демодуляторах сигналов КАМ-М.
Контрольные вопросы
1. Поясните работу схемы восстановления несущего колебания с умножением частоты.
2. Поясните, что такое неопределенность фазы опорного колебания.
3. Поясните, что такое детектор ошибки Костаса.
Дата добавления: 2016-07-27; просмотров: 2888;











