Фазоразностная модуляция

Устранить инверсную работу демодулятора ФМ-2 позволяет переход к разностному методу передачи, при котором передаваемые двоичные символы (биты) отображаются не в начальные фазы канальных символов (как при
ФМ-2), а в разность фаз соседних во времени канальных символов. Формирование модулированного сигнала таким способом называется фазоразностной модуляцией – ФРМ-2.

Принцип формирования и демодуляции сигналов ФРМ-2 отображен на рис. 14.1. Модулятор сигнала ФРМ-2 состоит из разностного кодера (РК) и модулятора сигнала ФМ-2, а демодулятор сигнала ФРМ-2 – из демодулятора сигнала ФМ-2 и разностного декодера (РД).

Разностный кодер модема ФРМ-2 работает по правилу

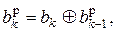(14.1)

где b_k – бит 1 или 0 на входе кодера на k-ом тактовом интервале;

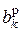– символ 1 или 0 на выходе кодера на k-ом тактовом интервале;

Å – знак сложения по модулю 2.

Разностный декодер модема ФРМ-2 работает по правилу

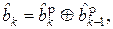(14.2)

где 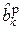– символ 1 или 0 на входе разностного декодера на k-ом тактовом интервале;

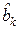– бит 1 или 0 на выходе разностного декодера на k-ом тактовом интервале.

Начальная фаза восстановленного несущего колебания в демодуляторе может совпадать с начальной фазой демодулируемого сигнала ФМ-2 или отличаться от нее на угол p. В общем виде можно записать, что фаза опорного колебания приобретает сдвиг p×p (p = 0 или 1 – значения, которые описывают сдвиг фазы). Считая, что помех в канале связи нет, символы на выходе демодулятора ФМ-2 будут определяться соотношением

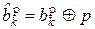(14.3)

для всех k. Подставив выражение (14.3) в формулу (14.1), легко убедиться, что бит 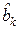не зависит от р.

Пример кодирования и декодирования произвольной последовательности бит приведен в табл. 14.1. Таблица иллюстрирует кодирование, начиная с k = 1. Поскольку при кодировании на k-ом тактовом интервале принимает участие предыдущий кодированный символ, то во второй строке произвольно принято 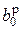= 0. Строка 3 повторяет строка 2 – демодуляция без обратной работы. Результат декодирования приведен в строке 4. Строка 5 содержит инверсию строки 2 – демодуляция с обратной работой. После декодирования восстановленный сигнал (строка 6) совпадает с исходным сигналом (строка 1). Таким образом, передача с разностным кодированием устраняет обратную работу демодулятора ФМ-2.

В случае М-ой фазовой модуляции по той же причине, что и в случае ФМ-2, имеет место неопределенность фазы порядка 2p/М. Аналогично ФРМ-2 информация отображается в разность фаз соседних канальных символов и имеет место ФРМ-М. При М > 2 разностный кодер и декодер работают из М-ми символами. Переход от бит цифрового сигнала к М-ым канальным символам происходит в кодере модуляционного кода.

При передаче цифровых сигналов сигналами ФМ-4 используются 4 канальных символа

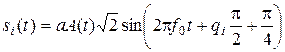, (14.4)

где q_i – четверичные символы, принимающие значения 0, 1, 2, 3;

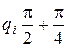– начальные фазы канальных символов, принимающие значения p/4, 3p/4, 5p/4, 7p/4.

Начальная фаза восстановленного в демодуляторе опорного колебания однозначно определенной быть не может – она определяется с точностью до p/2. Это обусловлено симметрией сигнального созвездия ФМ-4: при демодуляции неизвестно, какой из четырех сигналов считать “нулевым”.

Чтобы устранить влияние неопределенности фазы опорного колебания при демодуляции сигнала ФМ-4, переходят к модуляции ФРМ-4. Принцип формирования и демодуляции сигналов ФРМ-4 отображен на рис. 14.2. Модулятор сигнала ФРМ-4 состоит из кодера модуляционного кода, разностного кодера и модулятора сигнала ФМ-4, а демодулятор сигнала ФРМ-4 – из демодулятора сигнала ФМ-4, разностного декодера и декодера модуляционного кода. На этом рисунке и ниже по тексту нижний индекс k определяет номер тактового интервала, а сдвиг q может принимать значения 0, 1, 2 и 3.

Разностный кодер при ФРМ-4 реализует правило кодирования четверичных символов:

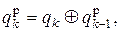(14.5)

где Å – сложение по модулю 4 (остаток от деления на 4 арифметической суммы слагаемых).

Разностный декодер реализует правило декодирования четверичных символов:

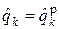y 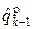, (14.6)

где y – вычитание по модулю 4 (остаток от деления разности на 4).

Начальная фаза опорного колебания в демодуляторе может совпадать с начальной фазой демодулируемого сигнала ФМ-4 или отличаться от нее на угол p×p/2 (p = 0, 1, 2 или 3 – значение, описывающее сдвиг фазы). Считая, что помехи в канале связи нет, символы на выходе демодулятора ФМ-4 будут определяться соотношением

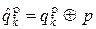(14.7)

для всех k. Таким образом, из-за неопределенности фазы когерентного колебания в демодуляторе сигнала ФМ-4 все символа 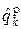получают приращение p. Если подставить выражение (14.7) в формулу (14.6), то легко убедиться, что символ 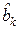не зависит от р.

При ФРМ-4 благодаря вычитанию в декодере значения p неопределенность фазы снимается. Поскольку для исключения неопределенности фазы значение 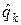определяется как разность двух соседних символов, то при кодировании значение 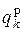формируется как сумма предыдущего значения 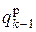и передаваемого символа q_k.

Правила сложения по модулю 4 приведены в табл. 14.2, а правила вычитания по модулю 4 – в табл. 14.3.

При передаче цифрового сигнала сигналом ФМ-4 переход от пар бит b₁b₂ к четверичным символам q на каждом тактовом интервале осуществляется согласно модуляционному коду Грея, пример которого приведен в табл. 14.4.

Поскольку при демодуляции сигнала ФМ-4 наиболее вероятные ошибки – это переходы в ближайшие сигналы, то при использовании кода Грея такие переходы приводят к ошибке лишь в одном бите, и, тем самым, минимизируется вероятность ошибки бита.

В табл. 14.5 приведен пример кодирования и декодирования при передаче цифрового сигнала методом ФРМ-4. Принято, что значение p = 3, а 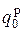= 1. Переход от пар бит к четверичным символам осуществляется согласно табл. 14.4. Из данных табл. 14.5 вытекает, что принятые биты совпадают с переданными.

Предположим, что из-за действия помехи демодулятор ФМ-2 выносит ошибочное решение на k-м тактовом интервале. Каждый символ, поступающий на вход разностного декодера, при декодировании используется дважды – на k-м и на (k + 1)-м тактовых интервалах. Поэтому, если решение демодулятора на (k – 1)-м и на (k + 1)-м тактовых интервалах верные, то на выходе разностного декодера появятся два ошибочных бита. Итак, разностный декодер размножает ошибки.

Вероятность ошибки бита при передаче методами ФРМ-2 и ФРМ-4 в области малых значений вероятности ошибки (р << 1) запишется

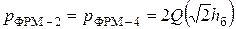. (14.8)

На завершение рассмотрения ФРМ-М отметим, что в русскоязычной литературе такой способ передачи называют также относительной фазовой модуляцией ОФМ-М).

Таблица 14.5 – Пример разностного кодирования и декодирование четверичных символов

Номер тактового интервала k
Последовательность переданных бит
Последовательность символов qk
Последовательность символов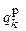
Последовательность символов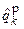
Последовательность символов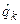
Последовательность принятых бит

Контрольные вопросы

1. Объясните принцип формирования и демодуляции сигнала ФРМ-2.

2. Объясните принцип формирования и демодуляции сигнала ФРМ-4.

3. Как определяется помехоустойчивость систем передачи методами ФРМ-2 и ФРМ-4?

15. Некогерентная демодуляция сигналов
цифровой модуляции

До сих пор мы рассматривали схемы демодуляторов, которые реализуют когерентную демодуляцию. Демодуляция сигналов называется некогерентной, если в демодуляторе не используются сведения о начальных фазах демодулируемых сигналов. Очевидно, что это возможно, по крайней мере, при демодуляции сигналов АМ-2 и ЧМ-2, в которых информация заложена в амплитуде и частоте канальных символов, соответственно, а не в их начальных фазах.

Цель использования некогерентной демодуляции – упрощение схемы демодулятора благодаря отсутствию схемы восстановления несущего колебания. Так, в случае сигнала АМ-2 схема демодулятора имеет вид (рис. 15.1).

Принципиальное отличие схемы некогерентного демодулятора (рис. 15.1) от когерентного – отсутствие синхронного детектора, который содержит схему восстановления несущего колебания. Вместо синхронного детектора используется детектор огибающей (ДО). При аналоговой реализации схема ДО выполнялась очень просто (рис. 15.2). При процессорной реализации огибающая вычисляется как корень квадратный из суммы квадратов квадратурных составляющих сигнала. Полосовой фильтр к детектору должен пропускать сигнал и ослаблять помехи на частотах, которые находятся вне полосы частот сигнала. Другие элементы схемы такие же, как и в схеме когерентного демодулятора.

Схема, приведенная на рис. 15.1, может использоваться и для демодуляции сигналов АМ-М, когда М > 2, но с ограничением на параметры: информационные коэффициенты a_i должны быть неотрицательными, так как выходное напряжение ДО не зависит от фазы канального символа. Созвездие сигнала АМ-4, для которого возможная некогерентная демодуляция, приведено на рис. 15.3.

Анализ помехоустойчивости системы передачи при некогерентной демодуляции затруднен, так как распределение помехи на выходе ДО существенным образом отличается от нормального. Однозначно можно сказать, что отношение сигнал/шум на выходе ДО в 2 раза меньше, чем на выходе синхронного детектора. Окончательная формула для вероятности ошибки бита на выходе демодулятора

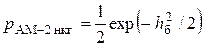. (15.1)

Канальные символы (радиоимпульсы) при ЧМ-2 отличаются частотами:

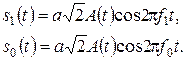(15.2)

В схеме когерентного демодулятора сигнала ЧМ-2 канальные символы разделяются синхронными детекторами. В схеме некогерентного демодулятора для их разделения используются полосовые фильтры (рис. 15.4).

Полосовые фильтры имеют средние частоты полос пропускания f₁ и f₀. Схема справа от детекторов огибающей в точности такая же как и в схеме когерентного демодулятора. Формула для вероятности ошибки бита на выходе демодулятора ЧМ-2 такая же, как и при АМ-2:

р_{ЧМ-2 нкг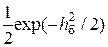} = . (15.3)

Возможна некогерентная демодуляция и сигнала ФРМ-2 в том понимании как определено выше понятие «некогерентная демодуляция» в начале подраздела. При ФРМ-2 информация заложена не в начальных фазах канальных символов, а в разность фаз соседних во времени символов. Поэтому можно, не зная начальные фазы канальных символов, выполнить демодуляцию путем сравнения фаз соседних символов. Схема некогерентного модулятора сигнала ФРМ-2 приведена на рис. 15.5.

В схеме демодулятора используется схема задержки на тактовый интервал. Можно считать, что на перемножителе выполнен синхронный детектор, где опорным колебанием является предыдущий канальный символ. Полярность напряжения на выходе перемножителя (и на выходах следующих блоков) зависит от разности фаз перемножаемых колебаний:

случай 1 – одинаковые фазы соседних символов:

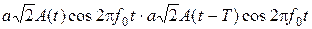= a²A(t)A(t – T) + a²A(t)A(t – T)cos2p2f₀t;

случай 2 – фазы соседних символов отличаются на p:

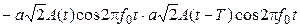= – a²A(t)A(t – T) – a²A(t)A(t – T)cos2p2f₀t.

Первые слагаемые создают на выходе СФ напряжения, полярность которых зависит от того, одинаковые или противоположные фазы перемножаемых колебаний. Из изложенного видно, что:

1) правило вычисления решений схемой решения (СР):

если 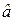> 0, то 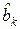= 0,

если 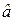< 0, то 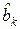= 1;

2) относительный декодер не требуется.

Распределение мгновенных значений шума на выходе перемножителя не является гауссовским из-за присутствия компоненты, порожденной произведением шумов n(t) и n(t – T). Анализ вероятности ошибки затруднен. Окончательная формула для вероятности ошибки бита на выходе демодулятора имеет вид:

Р_{ФРМ-2 нкг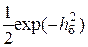} = . (15.4)

Отметим, что широко используется следующая терминология: некогерентную демодуляцию сигнала ФРМ-2 называют приемом по методу сравнения фаз; когерентную демодуляцию сигнала ФРМ-2 называют приемом по методу сравнения полярностей.

Сравним помехоустойчивость когерентных и некогерентных демодуляторов двоичных сигналов. Для сравнения используем зависимости р = 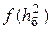(рис. 15.6).

Из рисунка видно, что при переходе от когерентной демодуляции к некогерентной для сохранения вероятности ошибки необходимо увеличить отношение сигнал/шум приблизительно на 1 дБ.

Некогерентная демодуляция широко использовалась многие десятилетия, когда аппаратура выполнялась на радиолампах и транзисторах. Ныне некогерентная демодуляция используется ограниченно, например, если в канале связи быстро изменяется начальная фаза сигнала – радиосвязь между объектами, которые взаимно быстро перемещаются.

Контрольные вопросы

1. Объясните принцип некогерентной демодуляции сигналов АМ-2, ЧМ-2 и ФРМ-2.

2. Сравните помехоустойчивость когерентного и некогерентного способов демодуляции сигналов АМ-2, ЧМ-2 и ФРМ-2.