Матричное представление линейных кодов

В п. 2.3.2 образующая матрица (2.13) составлена путем простого подбора КВ в соответствии с предъявляемыми к ним требованиями. Такое решение задачи приемлемо при небольшом объеме кода, но становится малопригодным при его существенном увеличении. Соответственно, возникнут трудности и при составлении контрольной матрицы H.

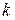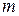Для упрощения указанных операций групповые коды удобно задавать матрицами, размерность которых определяется параметрами кода и . Число строк матрицы равно 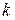, число столбцов равно .

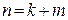Теорией и практикой установлено, что для упрощения процесса кодирования наиболее удобно, чтобы порождающая матрица 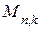состояла из двух матриц: единичной матрицы размерности 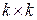и дописываемой справа матрицы-дополнения (контрольной подматрицы) размерности 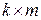, которая соответствует 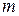проверочным разрядам:

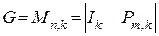(2.22)

Единичной матрицей I называется квадратная матрица, у которой по одной из диагоналей расположены только единицы, а все остальные элементы равны нулю.

При составлении матрицы 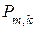рекомендуется из всех возможных m-значных кодовых комбинаций в качестве строк матрицы 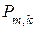выбирать комбинации, обладающие наибольшим весом. Это обеспечивает требуемое кодовое расстояние между КВ матрицы 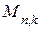, а использование в 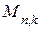единичной матрицы 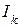гарантирует их линейную независимость.

По известной матрице 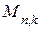контрольная матрица Н определяется в соответствии с выражением:

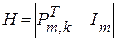, (2.23)

где 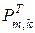– транспонированная матрица 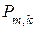(в транспонированной матрице строками являются столбцы, а столбцами – строки исходной матрицы );

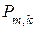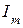– единичная матрица размером .

Пример. Построить контрольную матрицу Н для линейного 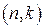-кода, исправляющего все одиночные ошибки, если требуемый объем кода Q=25.

Решение:

1. Определяем требуемое число информационных разрядов

,

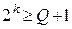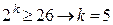
2. Определяем требуемое число контрольных разрядов m в соответствии с (2.11):

.

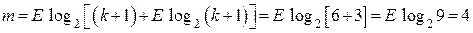Следовательно, . Код .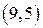

Строим матрицу 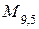в соответствии с (2.22):

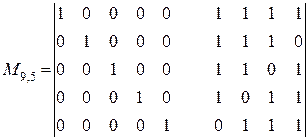(2.24)

По известной матрице 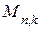строим контрольную матрицу в соответствии с (2.23):

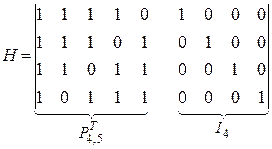(2.25)

Циклические коды

Групповой год называется циклическим, если все КВ, составляющие образующую матрицу, могут быть получены циклическим сдвигом одной образующей комбинации кода.

При циклическом сдвиге все символы кодовой комбинации перемещаются справа налево на одну позицию, причем крайний левый символ каждый раз переносится в конец комбинации.

Запишем, например, образующую (производящую) матрицу G, получающуюся при циклическом сдвиге комбинации 0 0 1 0 1 1:

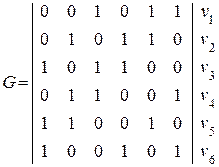(2.26)

КВ, входящие в образующую матрицу G, являются разрешенными. Остальные разрешенные КВ получаются путем суммирования по модулю 2 всех возможных комбинаций КВ, входящих в образующую матрицу G.

При описании циклических кодов n-разрядные кодовые комбинации представляются в виде многочленов фиктивной переменной x, в которых коэффициентами при переменной x являются цифры 0 и 1, составляющие КВ. Например, КВ 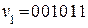в виде многочлена представляется так:

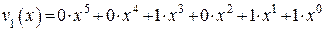
Члены с нулевыми коэффициентами при записи опускаются, т.е. 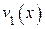имеет вид: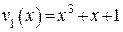

В общем случае, если число элементов КВ равно n, соответствующий ему многочлен имеет вид:

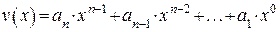, (2.27)

где 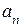, ,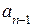…, 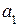– – коэффициенты, принимающие значения 0 и 1.

Наибольшая степень x в слагаемом с ненулевым коэффициентом называется степенью многочлена.

Замена кодовых комбинаций многочленами позволяет заменить действия над КВ действиями над многочленами, с которыми можно производить все обычные алгебраические операции, за исключением операций сложения и умножения.

Теория циклических кодов базируется на теории групп и теории колец, где определены операции символического сложения и умножения.

Сложение, как уже отмечалось, должно осуществляться по модулю 2.

Операция символического умножения задается так:

- многочлены перемножаются по обычным правилам, но с приведением подобных членов по модулю 2;

- если старшая степень произведения не превышает 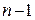, то оно и является результатом символического умножения;

- если старшая степень произведения больше или равна n, то многочлен произведения делится на многочлен 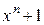(сам остаток в этом случае называется вычетом).

Учитывая изложенные особенности операций сложения и умножения многочленов, правила циклического сдвига КВ образующей матрицы можно сформулировать следующим образом.

Циклический сдвиг КВ с нулем в старшем разряде (слева) равносилен умножению многочлена, отображающего этот КВ, на x.

Циклический сдвиг КВ с единицей в старшем разряде равносилен умножению многочлена, отображающего этот КВ, на х с одновременным вычитанием из результата многочлена .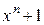

Пусть исходным является вектор 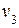матрицы (2.26). Тогда, согласно сформулированному правилу,

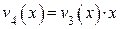
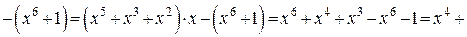
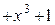(знак перед 1 заменен с «–» на «+» потому, что «–» здесь не имеет смысла). .

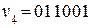В случаях, когда степень произведения равна n, операция вычитания из произведения многочлена 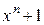эквивалентна делению этого произведения на 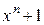, что предусмотрено общим правилом символического умножения.

За разрешенные кодовые комбинации в циклических кодах принимаются комбинации, которые делятся без остатка на некоторый заранее выбранный образующий многочлен.

При декодировании принятый КВ делится на образующий многочлен. Если принятый КВ имеет ошибку, то деление производится с остатком. Сам факт появления остатка свидетельствует об ошибке, а анализ остатка позволяет локализовать и исправить ошибку.

Из сказанного следует, что образующий многочлен в циклических кодах выполняет такую же роль, что и контрольная матрица в рассмотренных выше линейных кодах.