Синдромный метод декодирования
Декодирование линейных кодов, так же как и кодирование, основано на использовании контрольной матрицы 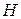 . Наиболее распространенным методом декодирования является метод синдромного декодирования. Данный метод основан на использовании так называемых синдромов ошибок, представляющих собой m-значные двоичные числа, разряды которых являются скалярными произведениями векторов ошибок на векторы контрольной матрицы.
. Наиболее распространенным методом декодирования является метод синдромного декодирования. Данный метод основан на использовании так называемых синдромов ошибок, представляющих собой m-значные двоичные числа, разряды которых являются скалярными произведениями векторов ошибок на векторы контрольной матрицы.
Вектор ошибки представляет собой n-значное двоичное число, содержащее 1 в разряде, где есть ошибка, и 0 во всех остальных разрядах. В качестве примера найдем синдром ошибки в 3-м разряде:
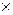
| – 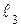
| 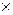
| – 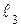
| 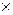
| – 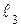
| |||||
– 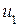
| – 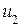
| – 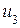
| ||||||||
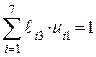
| 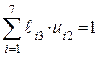
| 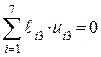
|
Итак, синдромом ошибки в 3-м разряде является комбинация 110. Действуя аналогично, можно найти синдромы ошибок во всех остальных разрядах. Характерным является то, что синдром ошибки i-го разряда совпадает с i-м столбцом контрольной матрицы, поэтому в запоминающем устройстве декодера достаточно хранить только контрольную матрицу.
При приеме с помощью принятого КВ и векторов контрольной матрицы вычисляется синдром. Если ошибки нет, то синдром будет нулевой. Во всех остальных случаях получается синдром, совпадающий с синдромом ошибки в соответствующем разряде. Это следует из того, что искаженную кодовую комбинацию 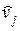 можно представить как сумму по модулю 2 вектора ошибки
можно представить как сумму по модулю 2 вектора ошибки 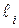 и неискаженного КВ
и неискаженного КВ 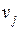 , т.е.
, т.е. 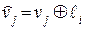 . Умножив искаженный КВ на векторы контрольной матрицы
. Умножив искаженный КВ на векторы контрольной матрицы 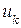 ,
, 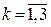 , получим:
, получим:
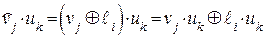 .
.
Но 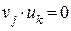 в силу ортогональности разрешенных КВ и векторов контрольной матрицы. Следовательно,
в силу ортогональности разрешенных КВ и векторов контрольной матрицы. Следовательно, 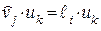 , что и требуется. Таким образом, определив синдром принятой комбинации можно однозначно указать номер разряда, в котором произошла ошибка.
, что и требуется. Таким образом, определив синдром принятой комбинации можно однозначно указать номер разряда, в котором произошла ошибка.
Пример 1
Из канала связи поступила комбинация 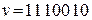 . Контрольная матрица имеет вид:
. Контрольная матрица имеет вид:
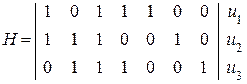 (2.19)
(2.19)
Определить, какое число передавалось.
Решение
1. Определяем синдром:
| – 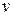
| 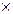
| – 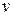
| 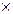
| – 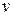
| |||||
– 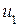
| – 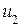
| – 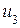
| ||||||||
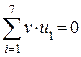
| 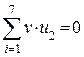
| 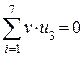
|
Итак, синдром ошибки 000, значит, передача прошла без искажений.
2. По матрице  определяем расположение контрольных разрядов и отбрасываем их:
определяем расположение контрольных разрядов и отбрасываем их:
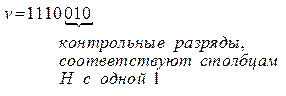
3. Находим десятичный эквивалент:
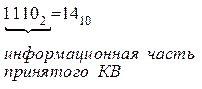
Пример 2.
Из канала связи поступила комбинация 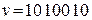 . Контрольная матрица та же, что и в примере 1. Определить, какое число передавалось.
. Контрольная матрица та же, что и в примере 1. Определить, какое число передавалось.
Решение
1. Определяем синдром:
| – 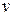
| 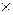
| – 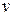
| 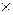
| – 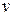
| |||||
– 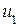
| – 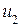
| – 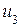
| ||||||||
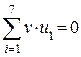
| 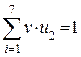
| 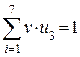
|
Итак, синдром ошибки 011. Не нулевой, следовательно, есть ошибка.
2. По контрольной матрице выясняем, что синдром совпадает со вторым столбцом, значит, ошибочным является 2-ой разряд принятого КВ.
3. Инвертируем искаженный разряд: 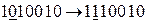 .
.
4. Отбрасываем контрольные символы и переводим информационную часть в десятичное число: 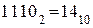 .
.
Дата добавления: 2019-02-08; просмотров: 1160;











