Построение эффективного кода по методам Шеннона-Фано и Хаффмена

Из теоремы Шеннона следует, что для обеспечения минимальной средней длины кодовых комбинаций эффективный код должен строиться так, чтобы символы кодовых комбинаций были равновероятны и статистически независимы друг от друга. Если требования независимости и равновероятности символов по каким-либо причинам невыполнимы, то, чем лучше они выполняются, тем ближе код к оптимальному. Именно эти соображения и используются при построении эффективного кода по методикам Шеннона-Фано и Хаффмена.

Код Шеннона-Фано строится следующим образом. Буквы первичного алфавита вписываются в таблицу в порядке убывания вероятностей. Затем они разделяются на две группы так, чтобы суммы вероятностей появления знаков в каждой из групп были по возможности одинаковы. Для всех букв верхней группы в качестве первого символа кодовой комбинации принимается 1, а для букв нижней группы – 0. В дальнейшем каждая из полученных групп разбивается на две по возможности равновероятных подгруппы и символ 1 или 0 (в зависимости от подгруппы) берется вторым элементом кодовой комбинации и т.д. Процесс повторяется до тех пор, пока в каждой подгруппе останется по одной букве.

Пример 1

Построить по методике Шеннона-Фано эффективный код для букв первичного алфавита, 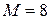. Вероятности появления букв в сообщениях:

; ;

.

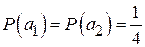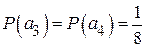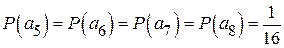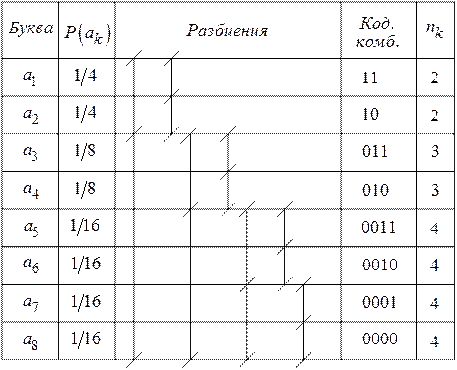
Процедура построения кода и результат приведены в таблице 2.1.

Из таблицы видно, что ни одна более длинная кодовая комбинация не является продолжением более короткой, следовательно, полученный код является разделимым.

Таблица 2.2

Процедура построения кода

Для определения того, является ли полученный код оптимальным или нет, необходимо сравнить значения реально полученной средней длины кодовой комбинации, вычисляемой в соответствии с (2.4), с минимально достижимой по теореме Шеннона. Имеем:

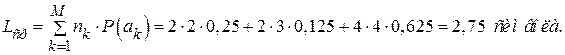
Так как вторичный код является двоичным , то минимальная средняя длина кодовой комбинации, определяемая по (2.5) и выраженная в символах, численно будет совпадать с энтропией первичного алфавита, выраженной в битах:

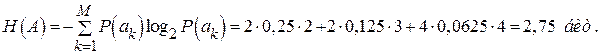
Таким образом, реально полученная средняя длина кодовой комбинации в точности равна энтропии первичного алфавита, выраженной в битах, следовательно, построенный код является оптимальным.

Для построения эффективного кода по методике Хаффменабуквы первичного алфавита вписываются в столбец в порядке убывания вероятностей (последнее не является обязательным, но желательно) и строится кодовое дерево в следующей последовательности. Сначала две буквы с наименьшими вероятностями объединяются в новую букву с вероятностью, равной сумме вероятностей объединенных букв. В дальнейшем новая буква и оставшиеся исходные буквы рассматриваются как равноценные и выполняется такая же процедура объединения. Этот процесс продолжается до тех пор, пока не получается единственная вспомогательная буква с вероятностью, равной 1.

При каждом парном объединении одна из ветвей кодового дерева обозначается символом 1, а другая 0. Код для каждой буквы представляет собой последовательности нулей и единиц, обозначающих ветви кодового дерева, по которым нужно пройти от вершины кодового дерева до данной буквы.

Пример 2

Для передачи сообщений используется алфавит из 5 знаков. Вероятности появления знаков: 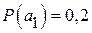; ; 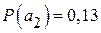; 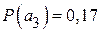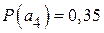. Определить вероятность появления знака 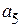и закодировать знаки первичного алфавита эффективным кодом по методике Хаффмена.

Решение. Эффективному кодированию подлежат только знаки, составляющие полную группу событий, т.е. 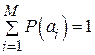. Следовательно, .

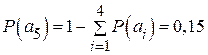Строим кодовое дерево:

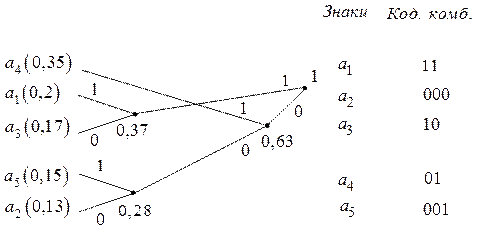
Проверка построенного кода на оптимальность осуществляется так же, как и в примере 1.