Примеры решения задач теории информации и кодирования
1. 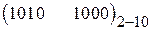 =
= 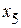
10 8
Задача поставлена некорректно, так как в десятичной системе коэффициент 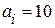 быть не может
быть не может 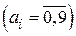 .
.
2. 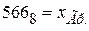
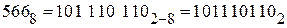
5 6 68
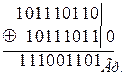
3. 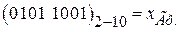
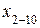 |
– | 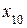 |
– | 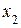 |
– | 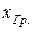 |
Схема решения:
| -58 | ||||||
| -28 | ||||||
| -14 | ||||||
| -6 | ||||||
| -2 | ||||||
1). 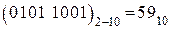 2).
2).
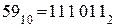
3). 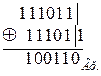
4. 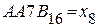 А=10, В=11.
А=10, В=11.
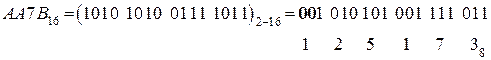
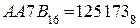
5. 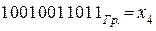
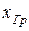 |
– | 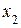 |
– | 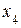 |
Схема:
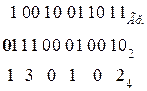
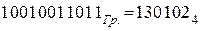
6. 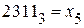 Задача поставлена некорректно, так как в троичной системе коэффициента
Задача поставлена некорректно, так как в троичной системе коэффициента 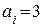 быть не может
быть не может 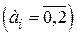 .
.
7. 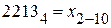
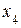 |
– | 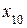 |
– | 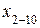 |
Схема:
1). По схеме Горнера: 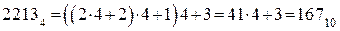
2). 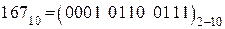
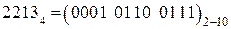
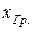 |
– | 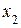 |
– | 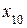 |
– | 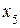 |
8. 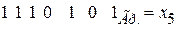 Схема:
Схема:
1). 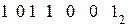
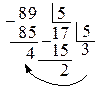 2).
2). 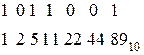 – по схеме Горнера
– по схеме Горнера
3). 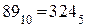
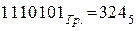
Пример задания по контрольной работе – часть 1
1. 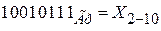
2. 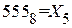
3. 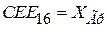
4. 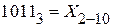
5. 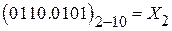
Контрольная работа – часть 2
В контрольную работу включены задачи из следующих разделов теории информации и кодирования:
1. измерение информации (аддитивная мера Хартли);
2. избыточность сообщений (абсолютная и информационная);
3. эффективное кодирование по методам Шеннона-Фано и Хаффмена;
4. кодирование и декодирование кодов, обнаруживающих ошибки (коды: с проверкой на четность; с числом единиц, кратным 3; корреляционный; комбинированный инверсный).
Краткие теоретические сведения
Информация по мере Хартли приведена в разделе 1.2 настоящих методических указаний (1.4).
Дата добавления: 2019-02-08; просмотров: 764;











