Классификация помехоустойчивых кодов

В настоящее время помехоустойчивые (корректирующие) коды используются как для обнаружения ошибок, так и для их исправления. Классификация корректирующих кодов представлена на рис. 2.1.

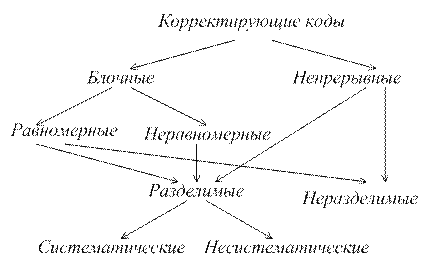
Рис. 2.1. Классификация корректирующих кодов

Как видно из рис. 2.1, все корректирующие коды делятся на два больших класса – блочные и непрерывные.

Блочные коды – коды, в которых каждому знаку сообщения в соответствие ставится кодовая комбинация из n символов, т.е. блок из n символов.

Блочный код называется равномерным, если значение n остается постоянным для всех знаков сообщения. В противном случае код называется неравномерным.

Непрерывные коды представляют собой непрерывную последовательность элементов, не подразделяемую на блоки. Процессы кодирования и декодирования здесь имеют непрерывный характер.

Блочные и непрерывные коды, в свою очередь, могут быть разделимыми и неразделимыми.

При кодировании разделимыми кодами в выходных последовательностях символов можно разграничить информационные символы и проверочные. В неразделимых кодах такое разграничение невозможно.

Разделимые коды делятся на систематические и несистематические.

Систематическими называются коды, в которых контрольные (проверочные) элементы представляют собой различные линейные комбинации информационных элементов. Несистематические коды таким свойством не обладают.

В настоящее время среди корректирующих кодов наибольшее распространение имеют блочные разделимые систематические коды.

2.2.6. Общие принципы использования избыточности
при построении корректирующих кодов

Предположим, что на вход кодера (кодирующее устройство) подана безизбыточная кодовая комбинация, состоящая из 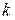информационных символов. В кодере по определенному алгоритму к поступившим 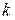символам добавляется 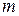контрольных символов. В результате на выходе кодера будет получена n-значная комбинация, где .

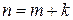При двоичном кодировании число различных кодовых комбинаций на входе кодера равно 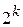, а возможное число n-значных кодовых комбинаций – 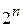. Очевидно, что из теоретически возможного множества n-значных комбинаций на выходе кодера реально существуют только 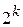комбинаций, соответствующих входным. Эти комбинации составляют подмножество разрешенных кодовых комбинаций. Остальные 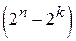возможных комбинаций для передачи не используются и образуют подмножество запрещенных кодовых комбинаций.

В процессе передачи информации по каналу связи в результате действия помех любая из 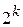разрешенных комбинаций может трансформироваться в любую из множества 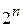. Таким образом, число возможных исходов передачи будет равно 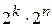. Из них:

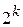случаев безошибочной передачи;

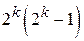случаев перехода одних разрешенных комбинаций в другие разрешенные комбинации, что соответствует необнаруживаемым ошибкам;

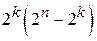случаев перехода в запрещенные кодовые комбинации, что соответствует обнаруживаемым ошибкам.

На приемной стороне множества разрешенных и запрещенных кодовых комбинаций известны, поэтому сам факт появления комбинации в подмножестве запрещенных является фактом обнаружения ошибки. Однако локализовать и исправить ошибку при этом невозможно.

Для исправления ошибки все множество запрещенных комбинаций разбивается на 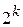непересекающихся подмножеств 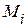, , 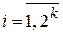каждое из которых ставится в соответствие одной из разрешенных комбинаций 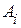. При получении запрещенной комбинации, принадлежащей подмножеству 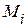, принимается решение, что передавалась комбинация 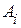. В данном случае ошибка будет исправлена, когда запрещенная комбинация действительно образовалась из разрешенной комбинации .

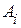Способ разбиения запрещенных кодовых комбинаций на непересекающиеся подмножества при данном виде исправления ошибок зависит от того, какие ошибки должны исправляться корректирующим кодом.

Большинство корректирующих кодов предназначено для исправления взаимно независимых ошибок определенной кратности или пакетов ошибок.

Кратностью ошибки называется количество искаженных символов в кодовой комбинации. При взаимно независимых ошибках вероятность искажения любых 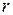символов в n-разрядной кодовой комбинации равна:

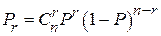(2.6)

где 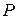– вероятность искажения одного символа.

Так как 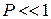, то из (2.6) следует, что наиболее вероятны ошибки малой кратности, т.е. при взаимно независимых ошибках наиболее вероятен переход в кодовую комбинацию, отличающуюся от данной в наименьшем числе символов.

Под пакетом ошибок подразумевается следующее. В реальных каналах связи длительность импульсов помехи часто превышает длительность одного символа, в результате одновременно могут исказиться несколько расположенных рядом символов кодовой комбинации.

Длиной пакета (пачки) ошибок называется число следующих друг за другом символов, левее и правее которых в кодовой комбинации искаженных символов не содержится.

Пример:

1 0 0	1 0 0 1 1 1 0	0 0 1	– исходная кодовая комбинация
1 0 0	0 1 0 0 1 0 1	0 0 1	– искаженная кодовая комбинация
	длина пакета ошибок

Теоретические исследования в области помехоустойчивого кодирования показали, что корректирующая способность кода прежде всего определяется кодовым расстоянием кода. Кодовое расстояние двух любых комбинаций характеризует степень различия этих комбинаций и равно числу символов, в которых комбинации отличаются одна от другой. Чтобы определить кодовое расстояние ( 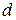), достаточно сложить кодовые комбинации по модулю 2 и подсчитать число единиц в сумме. Например:

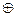
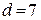
Под кодовым расстоянием кода подразумевается минимальное кодовое расстояние, определенное по множеству всех разрешенных комбинаций данного кода.

Рассмотрим на примере трехзначных кодовых комбинаций зависимость корректирующей способности кода от .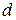

Пусть 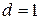. В этом случае все кодовые комбинации из множества 000, 001, 010, 011, 100, 101, 110, 111 являются разрешенными и любая одиночная ошибка переводит одну разрешенную комбинацию в другую разрешенную. Это случай равнодоступного кода, не обладающего корректирующей способностью.

Если 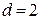, тогда множество всех возможных комбинаций 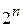, , 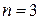разбивается на два непересекающихся подмножества: разрешенное и запрещенное. Пусть подмножество разрешенных комбинаций составляют комбинации 000, 011, 101, 110, 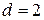. Тогда комбинации 001, 010, 100, 111 составят подмножество запрещенных кодовых комбинаций. Анализируя выделенные подмножества, можно видеть, что в данном случае однократная ошибка всегда переводит комбинацию из подмножества разрешенных в подмножество запрещенных, т.е. при 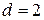код способен обнаруживать все одиночные ошибки.

В общем случае при необходимости обнаруживать ошибки кратности 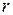кодовое расстояние кода должно быть больше 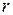по крайней мере на 1, т.е.

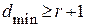(2.7)

Исправлять ошибки код с 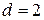не может, т.к. одна и та же запрещенная комбинация в данном случае может быть получена при однократной ошибке из различных разрешенных комбинаций. Для исправления одиночной ошибки каждой разрешенной кодовой комбинации необходимо сопоставить свое подмножество запрещенных комбинаций. Чтобы эти подмножества не пересекались, кодовое расстояние применяемого кода должно быть не менее 3.

При 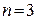из множества всех возможных комбинаций 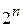можно выделить только две возможные комбинации с 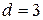, т.е. подмножество разрешенных кодовых комбинаций содержит не более 2-х комбинаций. Каждой из выбранных разрешенных комбинаций в соответствие ставится свое подмножество запрещенных кодовых комбинаций, отличающихся от разрешенной только в одном символе. Например, если в качестве разрешенных выбраны комбинации 000 и 111, то подмножество запрещенных кодовых комбинаций для 000 будет 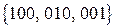, а для 111 – .

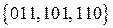Итак, код с 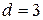способен исправлять однократную ошибку. В общем случае для исправления ошибки кратности минимальное кодовое расстояние между разрешенными кодовыми комбинациями, т.е. кодовое расстояние кода должно удовлетворять соотношению:

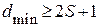(2.8)

В точке приема декодирование может производится таким образом, что принятая кодовая комбинация отождествляется с той разрешенной, которая отличается от полученной в наименьшем числе символов. Такое декодирование называется декодированием по методу максимального правдоподобия. Этот метод эффективно используется при обнаружении и исправлении ошибок заданной кратности, однако при исправлении пакетов ошибок более эффективными являются другие методы.

Если уровень помех в канале будет больше предполагаемого, то эффективность применения этого кода резко снизится.