Задачи на меру Хартли

Задачи на меру Хартли

1. Чему равно максимальное количество информации, переносимое 2 сообщениями 5-значного 8-ричного кода?

Решение: количество информации, переносимое 1 сообщением, определяется выражением: 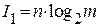. По условию задачи: , ,

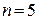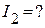
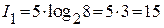бит. Количество информации, переносимое 2 сообщениями: бит.

2. Определить объем используемого алфавита, если известно, что 16-значное сообщение, составленное из этого алфавита, несет в себе 32 бита информации.

Решение: по условию задачи n=16, I=32 бита, m=?

, ; . .

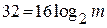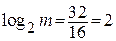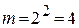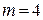3. Чему равна длина сообщения, составленного из 4-буквенного алфавита, если известно, что количество информации, переносимое 1 сообщением, равно 20 бит?

Решение: по условию задачи I=20 бит, m=4, n=?

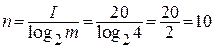; n=10.

Задачи на избыточность сообщений

1. Абсолютная избыточность сообщений, составленных из m-буквенного алфавита, равна 0,7 бит, а среднее количество информации, переносимое одним знаком сообщения, – 1,3 бита. Определить объем используемого алфавита.

Решение: абсолютная избыточность определяется выражением (2.1). 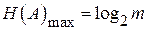, где 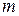– объем используемого алфавита. 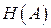определяет среднее количество информации. переносимое одним знаком сообщения. По условию задачи 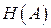=1,3 бит. Следовательно, 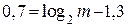. . m=4.

2. Информационная избыточность сообщений, составленных из 8-буквенного алфавита, равна 0,3. Определить среднее количество информации, приходящееся на 1 знак такого сообщения.

Решение: информационная избыточность определяется выражением 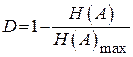; 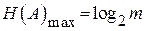. По условию задачи m=8; D=0,3. Следовательно, 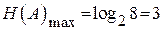. Среднее количество информации, приходящееся на 1 знак такого сообщения, 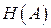= = 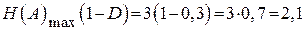бит.

3. В общем виде (не делать вычислений) записать выражения для информационной избыточности сообщений, составленных из алфавита п.2 (в п.2.1 приводятся вероятности появления букв, подлежащих эффективному кодированию).

Решение: информационная избыточность

=

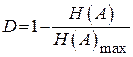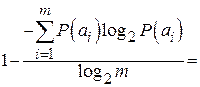
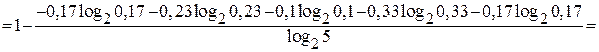
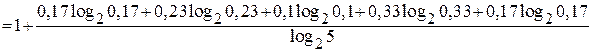
Задачи на эффективное кодирование

1. Закодировать по методике Хаффмена следующие буквы первичного алфавита 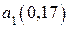, , 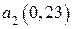, , 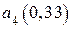. В скобках указаны вероятности появления букв в сообщении. Вероятность 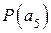определить.

Решение: эффективное кодирование применимо только к знакам, составляющим полную группу событий, т.е. 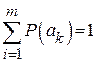. Следовательно, 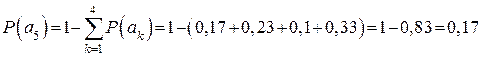. Располагаем подлежащие кодированию знаки в порядке убывания вероятностей и строим кодовое дерево.

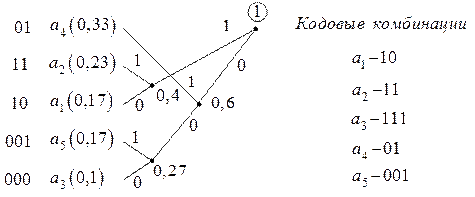
2. Закодировать по методике Шеннона-Фано следующие буквы первичного алфавита 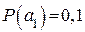, , 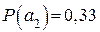, , 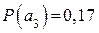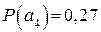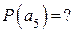. Вероятность 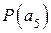определить.

Решение:

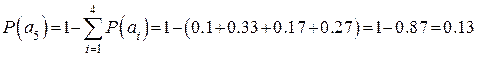
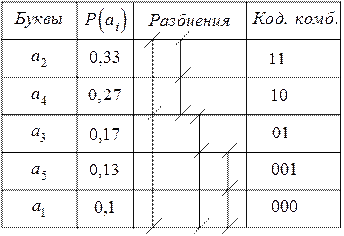
Задачи на кодирование обнаруживающими кодами

1.Закодировать кодом с проверкой на четность следующие комбинации:

а). 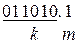; б).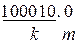

При любом числе информационных символов всегда контрольный символ выбирается таким, чтобы обеспечить четность 1 в полной комбинации.

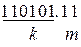2.Закодировать кодом с числом 1 кратным 3 следующие комбинации: а). ; б). ; с).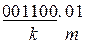

В данном коде всегда m=2, которые выбираются так, чтобы обеспечить вес полной комбинации кратным 3.

3.Корреляционный код (код с удвоением элементов). Каждый информационный символ представляется двумя символами: 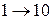, 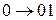. Если информационная комбинация имеет вид 01101, то в корреляционном коде ей будет соответствовать комбинация 0110100110.

4.В комбинированном инверсном коде 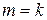. Кодирование осуществляется в следующей последовательности: сначала подсчитывается вес (число 1) в информационной части. Если он оказывается четным, тогда контрольная часть повторяет информационную, если нечетным – контрольная часть получается в результате инвертирования информационной:

1).

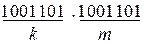
2).

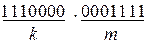
Задачи на декодирование обнаруживающих кодов

Во всех задачах на декодирование формулировка одинакова – приводится комбинация, поступившая из канала связи, указывается тип кода, используемого при кодировании, и предлагается определить число, переданное в канал связи.

Решение:

1. Если поступила комбинация в коде с проверкой на четность, нужно подсчитать число 1 в полной комбинации. Если оно оказалось нечетным, следовательно, произошла ошибка, которую данный код исправить не может (код только обнаруживает ошибки). Определить число, переданное в канал связи, невозможно.

Если число 1 в принятой комбинации четно, следовательно, ошибки нет. Контрольный разряд при этом отбрасывается (он не несет информации о числе), а оставшуюся информационную часть нужно перевести в десятичный код.

2. Если поступившая комбинация закодирована кодом с числом 1, кратным 3, проверяется вес полной комбинации на кратность 3. Если условие выполняется, контрольные разряды (два) отбрасываются, а оставшуюся часть переводят в десятичный код. В противном случае комбинация бракуется.

3. В случае применения корреляционного кода нужно последовательно, начиная со старших разрядов, проверять пары поступающих символов на четность. Если в результате этой проверки (например, с помощью сумматора по mod 2) во всех парах регистрируется нечетность (единицы), тогда четные символы отбрасываются, а оставшаяся информационная часть переводится в десятичный код. Если хотя бы в одной паре будет зафиксирована четность (0), комбинация бракуется.

4. Пример декодирования комбинации комбинированного инверсного кода приведен выше, где рассмотрен вопрос о его кодировании и декодировании. Следует помнить, что при отсутствии ошибки результатом декодирования будут 0 во всех разрядах. В этом случае контрольная часть отбрасывается, а информационная часть переводится в десятичный код.

Если в результате декодирования получены единицы и один 0, следовательно, произошла однократная ошибка в информационной части. Индикатором ошибочного разряда является 0. Данный разряд нужно инвертировать и исправленную таким образом информационную часть перевести в десятичный код.

Если в результате декодирования получены все 0 и одна 1, значит произошла однократная ошибка в контрольной части. Следовательно, информационная часть достоверна и ее следует перевести в десятичный код.

В случае, когда происходит многократная ошибка, результат декодирования не будет совпадать ни с одним из рассмотренных выше.