Коды, обнаруживающие ошибки

Код с проверкой на четность

Указанный код имеет в каждой кодовой комбинации всего один избыточный символ, т.е. 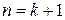. Общее число возможных выходных кодовых комбинаций в данном случае равно 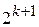. За подмножество разрешенных кодовых комбинаций можно принять, например подмножество 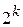комбинаций, содержащих четное число единиц. Тогда подмножество оставшихся 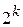комбинаций, содержащее нечетное число единиц, будет представлять собой подмножество запрещенных. При кодировании к каждой последовательности из 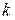информационных символов добавляется один символ (0 или 1), выбираемый таким образом, чтобы общее число единиц в последовательности оказалось четным. В таком случае искажение одного, а также любого нечетного числа символов переводит разрешенную кодовую комбинацию в подмножество запрещенных комбинаций с нечетным числом единиц и, таким образом, ошибка обнаруживается.

Код относится к классу разделимых и систематических. Проверочный символ в данном случае получается в результате суммирования информационных символов по модулю 2.

Пример

Пусть безизбыточная кодовая комбинация имеет вид .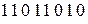

Проверочный символ 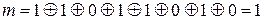, а кодовая комбинация на выходе кодера –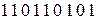

Код с числом единиц, кратным трем

Этот код образуется путем добавления к 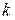информационным символам двух контрольных символов (m = 2), имеющих такие значения, при которых сумма единиц в разрешенных комбинациях кратна трем.

Пример

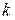
m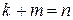

На приемной стороне вес полученных кодовых комбинаций проверяется на кратность 3 (вес кодовой комбинации – число ненулевых символов в комбинации).

Такой код позволяет обнаруживать все одиночные ошибки и любое четное количество ошибок одного типа (например, переход от 0 к 1).

Код относится к классу разделимых и систематических.

Корреляционный код

Корреляционный код по-другому называют кодом с удвоением элементов. Здесь каждый символ двоичного безизбыточного кода кодируется двумя элементами, причем 1 преобразуется в 10, а 0 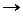01. Таким образом, вместо комбинации 01101, например, в канал связи передается 01.10.10.01.10. Ошибка обнаруживается, если в парных элементах будут содержаться одинаковые символы, т.е. 11 или 00 вместо 10 и 01. При правильном приеме четные элементы отбрасываются и остается первоначальная комбинация.

Код обладает высокой помехоустойчивостью, так как ошибка не обнаруживается только тогда, когда два рядом стоящих различных элемента, соответствующих одному информационному символу, будут искажены так, что 1 перейдет в 0, а 0 – в 1. Очевидно, что вероятность появления такого события невысокая.

Корреляционный код относится к группе разделимых и систематических.

Комбинированный инверсный код.

В таком коде к исходной 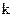-разрядной комбинации добавляется еще 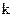контрольных символов. Правило образования кода следующее: если в исходной комбинации четное число единиц, то добавляемая комбинация повторяет исходную, если нечетное, то дополнительная комбинация – инвертированная исходная.

Пример

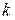
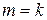
		Инверсный код
1 1 0 0 0 1	0 0 1 1 1 0	1 1 0 0 0 1 0 0 1 1 1 0
0 0 1 0 1 0	0 0 1 0 1 0	0 0 1 0 1 0 0 0 1 0 1 0

Прием комбинированного инверсного кода осуществляется в два этапа.

На 1-ом этапе суммируются единицы в первой (основной) группе символов 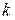. Если число единиц в этой части комбинации четное, то последующие контрольные символы принимаются без изменения; если число символов окажется нечетное, то контрольные символы инвертируются.

На 2-ом этапе контрольные символы 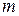сравниваются с информационными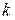 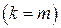путем суммирования по модулю 2. Если передача прошла без ошибок, то результат суммирования будет нулевым. В противном случае в сумме по модулю 2 появляются единицы, что и является индикатором ошибки.

Корректирующая способность кода очень высокая. Например, если в информационной части исказилось нечетное число разрядов, то ошибка будет не обнаружена только в случае, когда в проверочной части разряды, соответствующие ошибочным информационным, сохраняются неизмененными., а все остальные разряды инвертируются. Если же в информационной части искажается четное число разрядов, то ошибка не обнаруживается, когда будут искажены одноименные разряды и в проверочной части. Вероятность появления таких событий мала.

Рассматриваемый код способен не только обнаруживать многократные ошибки, но и исправлять однократные. При этом индикатором ошибочного разряда в информационной части является 0 при 1 во всех остальных разрядах суммы по 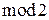, а индикатором ошибочного разряда в проверочной части является 1 при 0 во всех остальных разрядах указанной суммы.

Пример

Пусть исходная комбинация имеет вид:

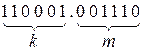
Предположим, что произошла однократная ошибка в информационной части, т.е. принята комбинация

После декодирования получаем:

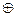
							– чт
							Вывод: ошибка в 4-м разряде информационной части

Если принята комбинация 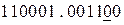, т.е. произошла ошибка в контрольной части, после декодирования получаем:

							– нч
							Вывод: ошибка в 5-м разряде проверочной части.

Комбинированный инверсный код относится к группе разделимых и систематических.