Теоретические основы эффективного кодирования

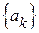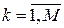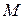Пусть требуется передать достаточно длинное сообщение, составленное из ансамбля знаков , , где – объем первичного алфавита: .

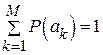При кодировании каждому знаку первичного алфавита ставится в соответствие своя кодовая комбинация во вторичном алфавите, содержащем 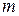символов. Обозначим через 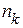длину кодовой комбинации, соответствующей знаку 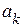, а через 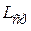– среднюю длину кодовой комбинации при выбранном способе кодирования. Тогда:

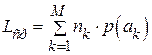(2.4)

При эффективном кодировании стремятся к тому, чтобы 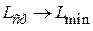. Это значит, что при определенном объеме передаваемой информации необходимо увеличивать ее количество на каждый символ сигнала, т.е. повышать, как обычно говорят, «плотность» упаковки информации.

Теоретической основой для определения минимально возможной средней длины кодовых комбинаций служит теорема Шеннона о кодировании при отсутствии помех. Теорема читается так: при кодировании множества сигналов с энтропией 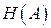в алфавите, насчитывающем 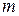символов, при условии отсутствия помех, средняя длина кодовых комбинаций не может быть меньше частного от деления указанной энтропии на количество информации в одном символе, т.е.

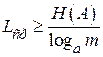(2.5)

Справедливость теоремы Шеннона можно видеть из следующих рассуждений.

Очевидно, что кодирование будет тем эффективнее, чем большее количество информации будет приходиться на каждый символ кодовой комбинации. Так как во вторичном алфавите 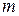символов, а максимальное количество информации в символе будет в случае, когда вероятности появления символов одинаковы, то максимально возможное количество информации, приходящееся на 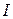символ кодовой комбинации, будет равно .

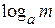Дополнительное сокращение времени, затрачиваемого на передачу сообщения, можно достигнуть с помощью специального кода, позволяющего вести передачу без промежутков между кодовыми комбинациями. Чтобы на приемной стороне можно было отличить одну комбинацию от другой, т.е. чтобы код был разделимым (однозначно декодируемым), он должен строиться так, чтобы ни одна более длинная кодовая комбинация не являлась продолжением более короткой. Например, при указанном кодировании нельзя применять комбинации 110 и 11010, так как вторая комбинация получена из первой путем добавления 10.