Регресія, що проходить через початок координат

Бувають випадки, коли PRF з двома змінними зображають у вигляді

.

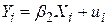(4.1.1)

У цій моделі параметр 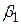, визначаючий точку перетину з віссю ординат, відсутній або дорівнює нулю. Така модель називається регресією, що проходить через початок координат.

Як ілюстрацію розглянемо модель оцінки капітальних активів ( Capital Asset Pricing Model) CAPM сучасної теорії портфеля, яка може бути подана у формі “ризик-премія”:

,

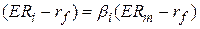(4.1.2)

де 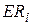– очікувана норма прибутку за цінними паперами i;

– очікувана норма прибутку на ринку портфеля, як наприклад фондовий індекс;

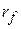– безризикова норма прибутку;

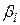– коефіцієнт, що являє собою міру систематичного ризику, тобто ризику, який не може бути виключений за допомогою диверсифікації. Це така міра впливу ринку на норму прибутку i-го цінного паперу. При 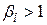говорять, що цінні папери нестійкі або агресивні, а при 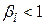- що вони захищені.

Якщо ринки капіталів працюють ефективно, то згідно з CAPM очікувана премія за ризик за і-ми цінними паперами 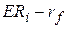дорівнює добутку відповідного 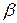-коефіцієнта на премію за ризик на ринку 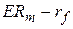. На рис.4.1 зображена лінія ринку цінних паперів.

Рівняння (4.1.2.) часто записують у вигляді

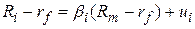
(4.1.3)

або

.

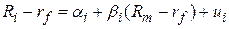(4.1.4)

Остання модель носить назву моделі ринку. Якщо САРМ виконується, то очікується, що 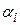повинен дорівнювати нулю.

Відзначимо, що в наведених рівняннях (4.1.3) і (4.1.4) залежна змінна Y є 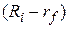, а пояснююча змінна Х є 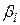, а не 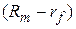. Отже, для складання рівняння регресії (4.1.4) необхідно спочатку оцінити 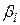, які звичайно виводяться з рівняння характеристичної лінії.

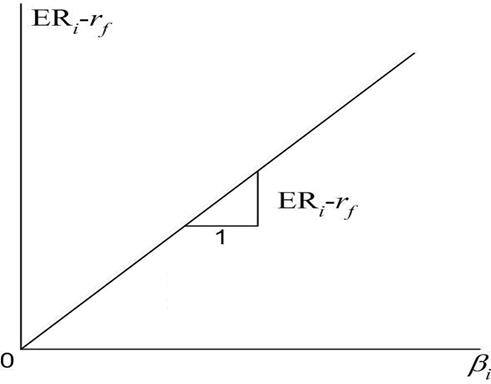
Рис.4.1. Лінія ринку цінних паперів

Як нам провести оцінку моделі, подібної (4.1.1), і які при цьому виникають особливості? Щоб відповісти на це питання, запишемо спочатку SRF моделі (4.1.1):

.

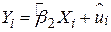(4.1.5)

Застосуємо метод найменших квадратів до (4.1.5), отримаємо таку формулу для 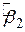і його дисперсії:

, ,

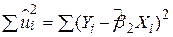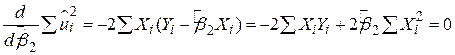звідси

.

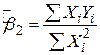(4.1.6)

Підставимо в (4.1.6) (4.1.5), одержимо

.

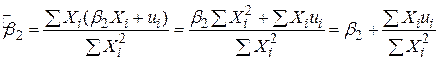Враховуючи незміщеність оцінки 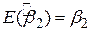, одержимо

.

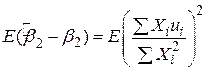Піднесемо у квадрат вираз, узятий у дужки в правій частині вищенаведеного рівняння. Оскільки 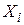передбачаються нестохастичними, використовуючи властивість гомоскедастичності і некорельованості відхилень 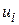, одержуємо

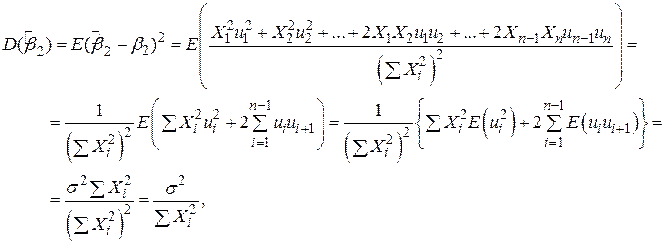
тобто

,

(4.1.7)

де оцінкою 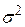служить

.

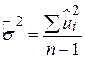(4.1.8)

Зауважимо, що при виведенні рівняння для визначення 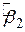, легко отримується рівність

.

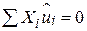Подібна рівність була виконана і для моделі, що містить 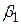. Нагадаємо, що для моделі, яка містить 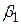, крім того виконувалася рівність 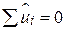. З вищезазначеного зрозуміло, що для регресії, яка проходить через початок координат, сума залишків 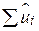не обов’язково дорівнює нулю.

Пригадаємо також, що 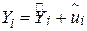. Підсумовуючи обидві частини рівності за всією вибіркою і розділивши потім на її обсяг, одержуємо

.

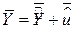Оскільки для моделі, що проходить через початок координат 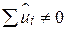, а отже і 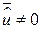, то

.

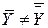Таким чином, у цьому випадку середнє фактичних значень Y не дорівнює середнім значенням за регресією. У цьому відмінність від властивостей моделі, що містить .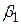

Цікаво порівняти формули (4.1.6)–(4.1.8) з отриманими для моделі з 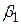, а саме з формулами (2.1.9), (2.3.1) і (2.3.5).

У моделі з 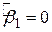є декілька моментів, про які слід згадати. 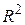, коефіцієнт детермінації, у випадку з 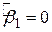може бути негативним. Тому, обчислений звичайним способом, він може не відповідати своєму значенню для регресії, що проходить через початок координат.

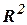для регресії, що проходить через початок координат

Як ми тільки що відзначили, звичайний коефіцієнт детермінації 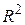, розглянутий нами раніше для моделі, що містить коефіцієнт 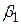, не придатний для регресії, що проходить через початок координат. Але можна обчислити так званий raw 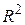(сирий) для такої моделі, якщо застосувати формулу

.

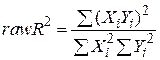(4.1.9)

Хоча цей raw 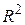задовольняє умову 0< 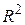<1, його не можна порівнювати безпосередньо зі звичайним 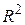. Тому деякі автори не наводять його для моделі з .

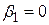Ураховуючи ці особливості, необхідно бути дуже обережним при використанні моделі з 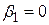. Якщо немає дуже вагомих підстав, краще використовувати звичайну модель, у якій наявний коефіцієнт 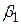. Це має подвійну перевагу. По-перше, якщо 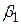включений у модель, але виявиться статистично не значимим (тобто таким, що статистично дорівнює нулю), то для практичних застосувань ми маємо регресію, що проходить через початок координат. Друге, і більш важливе зауваження, якщо в моделі насправді наявний 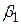, але ми не включили його і використовуємо модель з 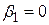, то ми допускаємо помилку специфікації моделі.