Тест на нормальність
Хоча в літературі обговорюється ряд тестів перевірки на нормальність, обмежимося розглядом двох: 1) тест  якості підгонки і 2) тест Jarque-Bera. Обидва ці тести використовують залишки
якості підгонки і 2) тест Jarque-Bera. Обидва ці тести використовують залишки 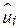 і розподіл імовірності
і розподіл імовірності  .
.
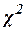 тест якості підгонки. Цей тест проводять таким чином. Спочатку ми отримуємо рівняння регресії, а також залишки
тест якості підгонки. Цей тест проводять таким чином. Спочатку ми отримуємо рівняння регресії, а також залишки 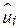 , підраховуємо стандартне відхилення
, підраховуємо стандартне відхилення 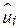 ((
(( 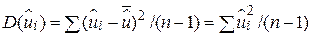 , оскільки
, оскільки 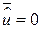 ). Потім упорядковуємо залишки і розміщуємо їх у різних групах (у нашому прикладі ми розміщуємо їх у шести групах), відповідних величині відхилення від нуля. Для нашого прикладу ми одержуємо такі дані (табл. 3.5).
). Потім упорядковуємо залишки і розміщуємо їх у різних групах (у нашому прикладі ми розміщуємо їх у шести групах), відповідних величині відхилення від нуля. Для нашого прикладу ми одержуємо такі дані (табл. 3.5).
Таблиця 3.5
Залишки для проведення  -тесту
-тесту
| Спостережувані залишки (Oi) | 0,0 | 2,0 | 3,0 | 4,0 | 1,0 | 0,0 |
| Очікувані залишки (Ei) | 0,2 | 1,4 | 3,4 | 3,4 | 1,4 | 0,2 |
| (Oi–Ei)2/Ei Sum=0,92 | 0,2 | 0,26 | 0,05 | 0,10 | 0,11 | 0,2 |
| (Oi–Ei)2/Ei Sum=0,92 | 0,2 | 0,26 | 0,05 | 0,10 | 0,11 | 0,2 |
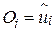 , де , де 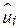 залишки за МНК залишки за МНК
|
У табл. 3.5 рядок, позначений як спостережувані залишки, дає частоту розподілу залишків для встановленого стандартного відхилення нижче і вище за нуль. У нашому прикладі немає залишків у два стандартних відхилення нижче нуля, 3 залишки між 1 і 2 стандартних відхилення нижче за нуль, 3 залишки між 0 і 1 стандартним відхиленням нижче за нуль, 4 залишки між 0 і 1 стандартним відхиленням вище за нуль, 1 залишок між 1 і 2 стандартними відхиленнями вище за нуль і жодного залишку, більшого за 2 стандартні відхилення вище за нуль.
Дані, поміщені в рядок очікуваних залишків, дають частоту розподілу залишків на основі передбачуваного закону розподілу ймовірності, у нашому випадку - нормального закону розподілу. У третьому рядку обчислюємо різницю між спостережуваними й очікуваними частотами, підносимо цю різницю у квадрат, ділимо результат на очікувану частоту і підсумовуємо. Алгебраїчний запис буде такий:
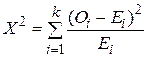 , ,
| (3.11.1) |
де 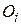 – спостережувана частота в класі або інтервалі i, Ei – очікувана частота в класі i на основі гіпотетичного розподілу, скажімо, нормального. Якщо різниця між спостережуваними й очікуваними частотами “мала”, то можна припустити, що відхилення
– спостережувана частота в класі або інтервалі i, Ei – очікувана частота в класі i на основі гіпотетичного розподілу, скажімо, нормального. Якщо різниця між спостережуваними й очікуваними частотами “мала”, то можна припустити, що відхилення 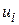 невеликі.
невеликі.
Дата добавления: 2016-07-27; просмотров: 1795;











