Сравнение двух дисперсий нормальных генеральных совокупностей

По независимым выборкам, объемы которых 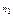и , и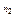звлеченным из нормальных генеральных совокупностей, найдены исправленные выборочные дисперси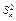и и .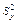

Требуется сравнить эти дисперсии.

Правило 1. Для того чтобы при заданном уровне значимости 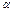проверить нулевую гипотезу H_о: D(X) = D(Y) о равенстве генеральных дисперсий нормальных совокупностей при конкурирующей гипотезе H₁: D(X)>D(Y), надо вычислить наблюдаемое значение критерия (отношение большей исправленной дисперсии к меньшей):

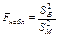
и по таблице критических точек распределения Фишера—Снедекора, по заданному уровню значимости 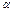и числам степеней свободы 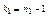, 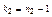(k₁ – число степеней свободы большей исправленной дисперсии) найти критическую точку 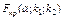. Если 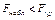нет оснований отвергнуть нулевую гипотезу. Если 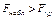– нулевую гипотезу отвергают.

Пример 9.3. По двум независимым выборкам, объемы которых 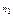=11 и 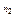=14, извлеченным из нормальных генеральных совокупностей X и Y, найдены исправленные выборочные дисперсии 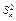= 0,76 и 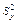= 0,38. При уровне значимости 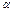= 0,05, проверить нулевую гипотезу H_о: D(X) = D(Y) о равенстве генеральных дисперсий, при конкурирующей гипотезе H₁: D(X)>D(Y).

Решение:

Найдем отношение большей исправленной дисперсии к меньшей:

.

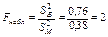По таблице (приложение 3), по уровню значимости 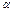= 0,05 и числам степеней свободы

,

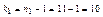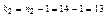
находим критическую точку

.

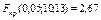Так как 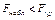– нет оснований отвергнуть гипотезу о равенстве генеральных дисперсий. Другими словами, выборочные исправленные дисперсии различаются незначимо.

Правило 2. При конкурирующей гипотезе H₁: D(X) 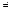D(Y), критическую точку 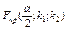ищут по уровню значимости 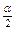(вдвое меньшему заданного) и числам степеней свободы k₁ и k₂ (k₁—число степеней свободы большей дисперсии). Если 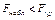нет оснований отвергнуть нулевую гипотезу. Если 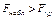– нулевую гипотезу отвергают.