Доверительные интервалы для оценки математического ожидания

нормального распределения при известном .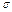

Пусть количественный признак X генеральной совокупности распределен нормально, причем среднее квадратическое отклонение 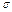этого распределения известно.

Требуется оценить неизвестное математическое ожидание а по выборочной средней 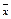. Тогда доверительные интервалы, покрывающие параметр а с надежностью 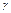, можно найти пользуясь формулами:

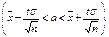
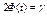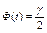где число t определяется из равенства или (по таблице Лапласа (приложение 2) находят аргумент t, которому соответствует значение функции Лапласа, равное ).

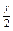Пример 8.1. Случайная величина X имеет нормальное распределение с известным средним квадратическим отклонением 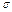= 3. Найти доверительные интервалы для оценки неизвестного математического ожидания а по выборочным средним 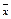, если объем выборки п = 36 и задана надежность оценки 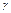= 0,95.

Решение.

Найдем t.

Из соотношения 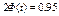получим 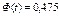. По таблице Лапласа находим t = l,96.

Найдем точность оценки:

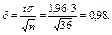
Доверительный интервал таков: ( 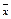– 0,98; 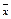+ 0,98). Например, если 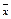= 4,1, то доверительный интервал имеет следующие доверительные границы:

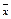– 0,98 = 4,1 – 0,98 = 3,12; 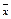+ 0,98 = 4,1 + 0,98 = 5,08.

Таким образом, значения неизвестного параметра а, согласующиеся с данными выборки, удовлетворяют неравенству 3,12 < а < 5,08.

Литература:

Гмурман, В. Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов/В. Е. Гмурман. — 9-е изд., стер. — М.: Высш. шк., 2003. — с.211 – 219.

Контрольные вопросы:

1. Как вы понимаете «найти статистическую оценку неизвестного параметра»?

2. Какие оценки называют несмещенными, эффективными?

3. Что представляет собой надежность оценки?

4. Что представляет собой доверительный интервал? Как его найти?