Правила комбинаторики

Подсчитать общее число возможных комбинаций помогает одно из важнейших правил комбинаторики — правило умножения: если первый элемент в комбинации можно выбрать m способами, после чего второй элемент — n способами, то общее число комбинаций из двух элементов будет m · n .

Пример 1.1. Подсчитаем количество двузначных чисел, которые можно составить из цифр 1, 2, 3. На первое место цифру можно выбрать тремя способами, после чего на второе место — тоже тремя способами. Значит, всего таких чисел по правилу умножения будет 3 · 3 = 9. Можно проверить ответ, выписав друг за другом все эти числа в порядке возрастания:

11, 12, 13;

21, 22, 23;

31, 32, 33.

В приведенном примере выбор второй цифры никак не связан с выбором первой. Но это далеко не всегда так.

Пример 1.2. Подсчитаем количество двузначных чисел, которые можно составить из цифр 1, 2, 3 так, чтобы все цифры были различны. На первое место цифру можно выбрать тремя способами, после чего на второе место — только двумя способами (ту цифру, которая на первом месте, использовать уже нельзя). Значит, всего таких чисел по правилу умножения будет 3 · 2 = 6. Вот эти числа:

12, 13;

21, 23;

31, 32.

Теперь в каждой из трех групп только по два элемента.

В данных примерах две принципиально различные схемы выбора элементов:

а) без возращения (повторений) элементов (это значит, что отбираются либо сразу все 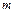элементов, либо последовательно по одному элементу, причем каждый отобранный элемент исключается из исходного множества);

б) с возвращением (повторением) элементов (выбор осуществляется поэлементно с обязательным возвращением отобранного элемента на каждом шаге и тщательном перемешиванием исходного множества перед следующим выбором).

Но бывают задачи, в которых после выбора одного из m объектов в качестве первого элемента комбинации нельзя однозначно сказать, сколькими способами можно выбрать второй элемент — это зависит от того, какой именно объект был выбран первым. Рассмотрим такую ситуацию на примере.

Пример 1.3. Подсчитаем количество двузначных чисел, которые можно составить из цифр 1, 2, 3 так, чтобы первая цифра была меньше второй. На первое место цифру можно выбрать тремя способами, а вот на второе место после этого:

– двумя способами, если первой цифрой была выбрана 1;

– одним способом, если 2;

– нулем способов, если 3.

Приходится применять комбинаторное правило сложения: разбить все комбинации на непересекающиеся классы, подсчитать количество комбинаций в каждом классе (например, по правилу умножения), а затем сложить эти количества.

В предыдущем примере количество комбинаций равно: 2 + 1 = 3.

Понятие факториала

п-факториал - произведение всех натуральных чисел от 1 до п включительно.

.

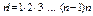Пример 1.4. 1) ,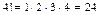

2) .

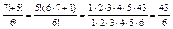Следует отметить, что 0! = 1.

Перестановки

Перестановки– комбинации из n элементов, которые отличаются друг от друга только порядком элементов. Общее число перестановок из n элементов обозначается 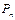и равно:

.

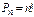Пример 1.5.Из букв A, B, C можно составить следующие перестановки:

ABC, ACB,

BAC, BCA,

CAB, CBA.

Всего перестановок 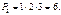Причем они отличаются друг от друга только порядком расположения букв.

Пример 1.6. Сколькими способами можно расставить на книжной полке собрание сочинений Диккенса, включающее 30 томов?

Решение:

Каждый такой способ — это перестановка из 30 элементов. Всего таких перестановок будет

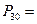30! = 265 252859 812191058636308 480 000000.

Число перестановок с повторениями можно найти применив формулу:

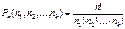
Размещения

Размещения – комбинации из n элементов по m элементов, которые отличаются друг от друга или самими элементами или их порядком.

Размещения обозначаются ,

где n – числи всех имеющихся элементов,

m – число элементов к каждой комбинации.

При этом полагают, что 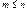. Число размещений можно вычислить по формулам:

.

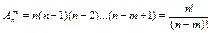Пример 1.7. Пусть имеются четыре буквы А, В, С, D. Составив все комбинации только из двух букв, получим: АВ, АС, АD,

ВА, ВС, ВD,

СА, СВ, СD,

DA, DB, DC.

Все полученные комбинации отличаются или буквами, или порядком (комбинации ВА и АВ считаются различными). Кратко это можно записать так:

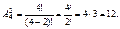
Пример 1.8. На книжную полку влезает только 8 любых томов из 30-томного собрания Диккенса. Сколькими способами можно заполнить этими томами такую полку?

Решение:

Каждый способ — это размещение из 30 элементов по 8. Всего таких размещений будет

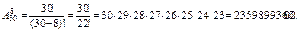
Число размещений с повторениями равно:

.

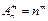Сочетания

Сочетания– все возможные комбинации из n элементов по m элементов, которые отличаются друг от друга по крайней мере хотя бы одним элементом.

Сочетания обозначаются 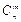и находятся по формуле:

.

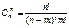Пример 1.9. Из четырех различных букв А, В, С, D можно составить следующие комбинации, отличающиеся друг от друга хотя бы одним элементом: АВ, АС, АD, ВС, ВD, СD.

Значит число сочетаний из четырех элементов по два равно 6.

Это можно найти и по вышеприведенной формуле:

Для сочетаний справедливы равенства:

,

,

.

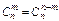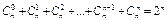Число перестановок, размещений и сочетаний связаны равенством:

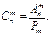
Литература:

1. Гмурман, В. Е. Теория вероятностей и математическая статистика: Учеб. пособие для вузов/В. Е. Гмурман. — 9-е изд., стер. — М.: Высш. шк., 2003. — с.22 – 23.

2. Гусак А.А. Теория вероятностей: справ. Пособие к решению задач / А.А. Гусак, Е.А. Бричикова. – 6-е изд. – Минск: ТетраСистемс, 2007. – с.13 – 21.

Контрольные вопросы:

1. В чем сущность комбинаторики?

2. Сформулируйте правило сложения.

3. Сформулируйте правило умножения.

4. В чем отличие выбора элементов с возращениями и без возращений?

5. Что называют перестановками?

6. По какой формуле вычисляют число перестановок из п различных элементов?

7. По какой формуле вычисляют число перестановок из п различных элементов с повторениями?

8. Что называют размещениями?

9. По какой формуле вычисляют число размещений из п различных элементов по m элементов?

10. Что называют сочетаниями?

11. По какой формуле вычисляют число сочетаний из элементов п различных элементов по m элементов?

12. Каким равенством связаны числа перестановок, размещений и сочетаний?

13. Чем отличаются сочетания от размещений? Что и во сколько раз больше?