Розрахунок повної кількості приходів робітників у комору

<16 17 181920 21 22 >

Кількість приходів в одиницю часу (за 15 хв.)	Кількість приходів, що спостерігається, %	Частота приходів, що спостерігається, %	Повна кількість приходів робітників (гр.1´гр.2)	Кількість приходів в одиницю часу (за 15 хв.)	Кількість приходів, що спостерігається, %	Частота приходів, що спостерігається, %	Повна кількість приходів робітників (гр.1 ´ гр.2)

						7,67
						6,67
		0,33
						5,33
		1,67				4,33
		2,67				3,67
		3,33				3,33
						2,67
		4,33				1,67
		5,33
						0,33
		6,67				0,33
		6,33				99,99

		8,33

Частота приходу двох робітників при 300 спостереженнях дорівнює 0,33 ´ ((1/300) ´ 100)), трьох – 1 ´((3/300 ´ 100))

Для визначення середньої кількості приходів в одиницю часу (l) обчислюється повна кількість приходів (N) як сума добутків кількості приходів (кількості робітників, що прийшли в комору) на кількість приходів, що спостерігається.

Таким чином, середня кількість вимог на обслуговування, тобто середня кількість приходів в одиницю часу (l), складе

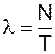(1.35)

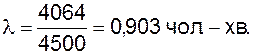
Щоб визначити розподіл імовірностей для тривалості обслуговування при припущенні, що закон розподілу експонентний, обчислимо середню тривалість одного обслуговування (Т_обсл) (вона дорівнює 1,6 хв.):

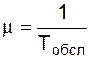(1.36)

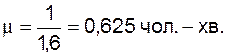
Після цього можна встановити інтенсивність обслуговування (µ).

У випадку, коли l < m , збільшення черги не виникає, тому що задоволення вимог відбувається не раніше їхнього надходження. У нашому прикладі l > m, (0,903 > 0,625) в коморі утвориться черга.

Точно визначити величину черги як випадкову не можна. Можна обчислити ймовірність того, що в момент часу (t) черга буде характеризуватися числом вимог Р_n (t):

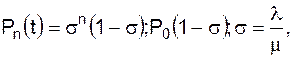(1.37)

де Р_n (t) – імовірність відсутності черги.

У тих випадках, коли s ³ 1, імовірність відсутності черги (s₀) звичайно береться з графіків (у нашому прикладі s = 1,445).

Для побудови таких графіків скористаємося таблицею значень Р₀ для різних значень s і n (n – кількість комірників в інструментальній коморі).

За даними табл. 1.11, у нашому випадку розглядається многолінійна система, коли n ³ 1 (кількість комірників перевищує одиницю).

Таблиця 1.11

Значення Р₀

						…
0,333	0,363	0,367	0,367	0,367	0,367	0,368
	0,111	0,130	0,134	0,135	0,135	0,135
		0,037	0,046	0,049	0,049	0,050
			0,013	0,016	0,017	0,018

Визначимо середній час чекання (Tс), що складається з середнього часу очікування обслуговування в черзі (Точ) і середнього часу обслуговування (Тобсл):

Тс = Точ + Тобсл . (1.38)

У тому випадку, коли в системі працює n комірників, середній час чекання в черзі визначиться за формулою:

при n = 2:

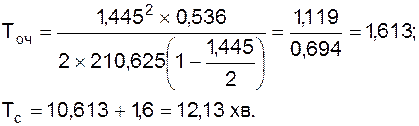
при n = 3:

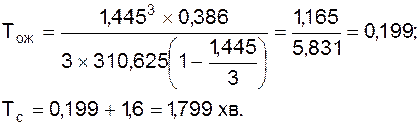
при n = 4:

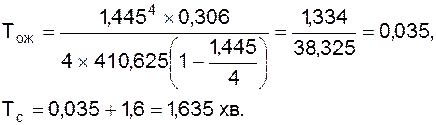
Припустимо, що у робітника витрати від простоїв складають 5, а утримання комірника – 4 гр. од. за одиницю часу. За період часу Т в систему надходить T заявок, тобто 1,445 T заявок.

Витрати внаслідок простою робітників при різному числі комірників, витрати на заробітну плату комірників, а також сумарні витрати і втрати наведені в табл. 1.12.

Таблиця 1.12

Витрати внаслідок простою робітників при різному числі комірників, витрати на заробітну плату комірників,
а також сумарні витрати і втрати

Кількість комірників	Втрати від простою робітників	Витрати на зміст комірників	Сумарні витрати і втрати
	3,213 ´1,445 ´ 5Т = 23,214Т	8Т	31,214Т
	1,799 ´ 1,445 ´ 5Т = 12,998Т	12Т	24,998Т
	1,635 ´ 1,445 ´ 5Т = 11,813Т	16Т	27,813Т

З табл. 1.12 випливає, що економічно вигідніше в інструментальній коморі мати трьох комірників, оскільки сумарні витрати і втрати будуть найменшими (min 24,998T).

Порядок обчислення показника якості обслуговування з явними втратами покажемо на прикладі для умов найпростішого потоку вимог.

Стіл замовлень при великому універсамі обладнаний чотирма телефонами. Середнє число викликів протягом години складає 96, середній час, витрачений на прийом одного замовлення – 2 хв. Потрібно визначити, наскільки завантажені приймальники замовлень, яка ймовірність відмови в обслуговуванні.

Ступінь завантаженості приймальників визначається за формулою:

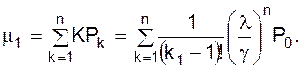(1.39)

За умовами прикладу n = 4 (4 телефони, 4 приймальника замовлень), l = 96 (число викликів протягом години); середній час, витрачений на прийом одного замовлення, складає 2 хв, чи 2/60 = 1/30 одиниці часу; значення параметра g = 1 : 1/30 = 30, отже, l/g = 96/30 = 3,2. Рівень імовірностей Р₀, Р₁, Р₂, Р₃наведені в табл. 1.10. Значення членів другого стовпця знайдено за формулою:

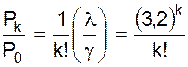. (1.40)

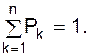
Як видно звідси,

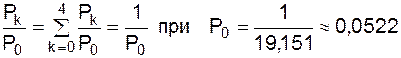
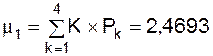Помножуючи кожне зі значень P_k на Р₀ = 0,0522, одержимо величину Р_k. Потім, помножуючи значення членів третього стовпця на значення членів першого стовпця (на 0), другого (на 1) тощо і підсумовуючи їх, одержимо математичне очікування кількості зайнятих приймальників (табл. 1.13).

Отже, кожен приймальник замовлень буде зайнятий у середньому 0,62 роб./дн. (2,4693/4)

Відповімо на друге питання: яка ймовірність відмовлення в обслуговуванні?

Для цього знайдемо ймовірність того, що всі приймальники будуть зайняті в момент звертання чергового клієнта:

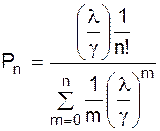. (1.41)