Мінімізація кількості внутрішніх станів автомата.

Ідея формальної процедури мінімізації кількості станів полягає в визначенні еквівалентних станів, де два стани є еквівалентними, якщо неможливо визначитись з різницею в їх функціонуванні, розглядаючи лише поточні і майбутні стани виходів автомата. Пара еквівалентних станів може бути замінена одним.

Існують детальні процедури, які дозволяють формально розв’язувати задачу мінімізації кількості станів, але на практиці вони рідко використовуються. Реально це обумовлено тим, що досвідчені інженери з електроніки проектують цифрові автомати з мінімальною кількістю станів без будь-яких проблем, не використовуючи формальні процедури. Більш того, часто мають місце ситуації, коли збільшення кількості станів не ускладнює проект, а, навпаки, спрощує його, і мінімізуючи процедури не надають необхідної користі.

Як правило, ПТП містить ряд збиткових внутрішніх станів, усунення яких не порушить алгоритму роботи автомата, але, в той же час, дозволить спростити його функціональну схему. В ряді випадків наявність збиткових станів не є очевидним фактом, тому для їх виявлення необхідно проводити детальний аналіз ПТП.

Скорочення частини станів асинхронного автомата базується на виявленні еквівалентних і псевдоеквівалентних станів, а також на виявленні і об’єднанні сумісних внутрішніх станів автомата (рядків ПТП).

Еквівалентними станами автомата називаються стійкі стани, які задовольняють наступним умовам:

1. Їм відповідає один і той же стан входу (тобто вони знаходяться в одному і тому ж стовбці ПТП);

2. Їм відповідає один і той же стан виходу (однакові вихідні сигнали автомата);

3. Будь-якій послідовності станів входу автомата відповідає одна і та ж сама послідовність станів його виходу, незалежно від того, який зі стійких станів автомата прийнято за початковий.

Розглянемо приклад.Автомат заданий ПТП, що приведена в табл. 6.4. Визначити еквівалентні та псевдоеквівалентні стани і скоротити кількість рядків ПТП.

Таблиця 6.4.

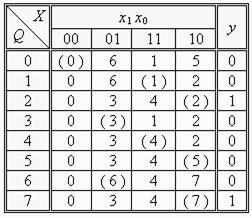
У відповідності до першої умови, еквівалентними можуть бути лише ті стани, які знаходяться в одному з стовбців таблиці, тобто стани (3) і (6); (1) і (4); (2) і (5); (2) і (7); (5) і (7).

З отриманих пар необхідно вибрати стани, що відповідають другій умові, тобто такі, яким відповідає один і той же стан виходу. Наприклад, стан 6 має значення виходу, що протилежний значенням (2) і (7). Тому можемо стверджувати, що стани (2) і (5), а також (5) і (7) не є еквівалентними. З пар станів, що залишилися – (3) і (6); (1) і (4); (2) і (7) – еквівалентними будуть ті стани, які відповідають ще й третій умові еквівалентності.

Для того, щоб два стійкі стани задовольняли третій умові еквівалентності, в одному і тому ж стовпці відповідних їм рядків повинні знаходитись одні і ті ж цифри або різні цифри, але визначаючі еквівалентні стани. У прикладі, що розглядається, еквівалентними будуть стійкі стани (2) і (7); (1) і (4); (3) і (6).

Після того, як еквівалентні стани виявлені, їх об’єднують. При цьому кожній групі еквівалентних станів приписують один номер, а всі рядки, в які входять еквівалентні стани однієї групи, замінюються одним рядком. У розгляданому прикладі стійкий стан (7) замінюється на (2); (6) – на (3); (4) – на (1). Так само перенумеровуються і нестійкі стани 7, 6 і 4 відповідно на 2, 3, 1.

В результаті отримуємо таблицю зі скороченою кількістю станів (табл. 6.5).

Таблиця 6.5.

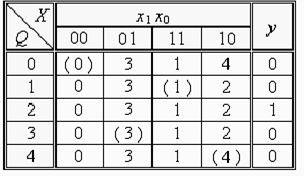
Для співпадіння номерів стійких станів з номерами рядків у табл. 6.5 необхідно стани 5 і (5) перенумерувати на 4 і (4).

Для неповністю визначеного автомата, окрім поняття еквівалентності, існує і використовується поняття псевдоеквівалентності станів. Псевдоеквівалентними називаються такі два стійкі стани автомата, яким:

· відповідає один і той самий стан входу автомата;

· відповідають стани виходів автомата, між якими немає протиріччя;

· будь-якій послідовності станів входу автомата відповідають непротирічні послідовності станів його виходу, незалежно від того, який з цих стійких станів взятий за початковий. Іншими словами, серед пар послідовностей станів входу і виходу, що починаються з цих стійких станів, не повинно бути таких, що мають протиріччя.

Після об’єднання еквівалентних і псевдоеквівалентних станів завжди отримується таблиця, в кожному рядку якої, як і в ПТП, знаходиться лише один стійкий стан. Скорочення кількості рядків, порівняно з ПТП, відбувається за рахунок зменшення кількості стійких станів. Але після об’єднання стійких станів можливо виконати подальше спрощення таблиці переходів за рахунок об’єднання сумісних внутрішніх станів автомата.

Під сумісним внутрішнім станом розуміють два або більше станів, яким відповідають рядки з розміщенням цифр в них, яке не має протиріччя, тобто такі рядки, в одному і тому ж стовбці яких знаходяться однакові цифри (або в одному рядку цифра, а в іншому – риска).

Строчки таблиці переходів, що відповідають сумісним станам, можуть бути об’єднані в одну. В об’єднаній строчці повинні бути стійкими стани у будь-якій з об’єднаних строчок. Тобто, при об’єднанні сумісних станів отримуємо таблицю, в кожній строчці якої може бути декілька стійких станів. При об’єднанні сумісних станів буде отриманий автомат, еквівалентний вихідному.

Об’єднання строчок з поєднаними стійкими станами виконується на основі наступних правил:

· дві або більше строчок можуть бути об’єднані, якщо значення вихідних змінних (станів виходу) для цих строчок не мають протиріччя для автомата Мура і можуть бути будь-якими для автомата Мілі, а номери станів, що записані в одних і тих же стовпцях, співпадають між собою, або з прочерком;

· при об’єднанні станів з однаковими номерами в дужках і без них результуючий стан повинен бути у дужках;

· якщо при об’єднанні станів в одному з рядків знаходиться прочерк, а в іншій – номер стану, то в скороченій таблиці пишеться номер стану.

Слід відмітити, що виявляти і об’єднувати еквівалентні і псевдоеквівалентні стани перед виявлення і об’єднанням сумісних станів немає потреби. Можна починати з виявлення і об’єднання сумісних внутрішніх станів. При цьому об’єднуються, якщо вони є, еквівалентні і псевдоеквівалентні стани. Більш того, у ряді випадків першочергове об’єднання псевдоеквівалентних станів недовизначеного автомата може ускладнити остаточне рішення, тобто може бути отриманий автомат з більшою кількістю внутрішніх станів, порівняно з автоматом, для якого зразу об’єднувались сумісні внутрішні стани.

Суттєву допомогу при аналізі сумісності строчок ПТП можуть надати діаграми (графи) сумісності внутрішніх станів, на яких сумісні стани розміщуються у вузлах, з’єднаних ненаправленими лініями. Множина внутрішніх станів є сумісною, якщо всі її стани є попарно сумісними. Таку множину можна замінити одним станом. Вибираючи мінімальну кількість таких множин, які охоплюють всі стани без їх повторення, отримують мінімальну кількість станів, яка достатня для реалізації автомата.

Для забезпечення знаходження максимальних множин сумісних станів іноді використовується трикутна таблиця сумісності, з правилами побудови якої можна ознайомитись, наприклад, в [Баранов С.И. Синтез микропрограммных автоматов (граф-схемы и автоматы). – Л.: Энергия, 1979. – 232 с.], [Трачик В. Дискретные устройства автоматики. – М.: Энергия, 1978. – 456 с.].

В якості прикладу розглянемо спосіб отримання скороченої (мінімальної) таблиці переходів з ПТП, що отримана для генератора з забороною (див. табл. 6.2). Аналіз цієї ПТП показує, що в ній відсутні еквівалентні і псевдоеквівалентні стани. Сумісними будуть наступні множини станів: { (0), (2) }; { (2), (5) }; { (2), (3), (5) }. Діаграма сумісності зображена у вигляді ненаправлених графів на рис. 6.3.

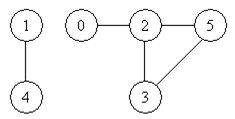
Рис.6.3. Діаграма сумісності станів

Аналіз діаграми сумісності показує, що є можливість виділити дві групи множин сумісності:

1. { (0), (2) }; { (1), (4) }; { (3), (5) };

2. { (0) }; { (1), (4) }; { (2), (3), (5) }.

В обох випадках кількість множин дорівнює трьом. Це означає, що в скороченій таблиці переходів повинно бути три внутрішніх стани.

Скорочена таблиця переходів, яка побудована на основі першого варіанта об’єднання станів, приводиться в табл. 6.6. Вона містить три рядки, що дає можливість побудувати автомат з трьома внутрішніми станами.

Таблиця 6.6.

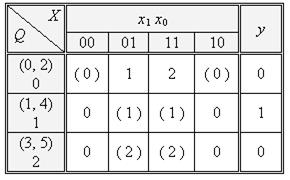
Об’єднання строчок слід виконувати у декілька етапів. Спочатку об’єднувані строчки зводяться в один, з меншим номером, і всі стани, що мають старші номери, замінюються на молодші. Так, при об’єднанні строчок 0 і 2 двійки другого стовпця замінюються на нулі. Якщо в одній з об’єднуваних строчок маємо невизначений стан, то при об’єднанні він замінюється визначеним (стовпець при 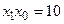має невизначений стан у другій строчці). Після об’єднання сумісних строчок виконується їх перейменування (в даному прикладі 3-я строчка замінюється на строчку з номером 2), а потім перейменовуються всі відповідні стани на нові номери (трійки замінюються на двійки).

Розглянемо ще один приклад. Автомат задається часовими діаграмами, що приведені на рис. 6.4. Побудувати початкову таблицю переходів, діаграму сумісності внутрішніх станів та мінімальну таблицю переходів.

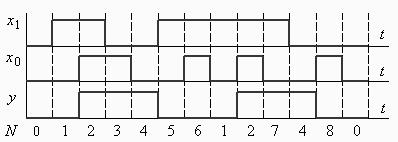
Рис.6.4.

Перенумеруємо всі комбінації вхідних сигналів 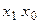і вихідного у, які мають місце на інтервалі повторюваності. Таких комбінацій маємо 9.

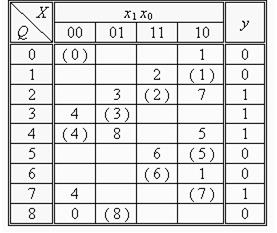
Таблиця 6.7.

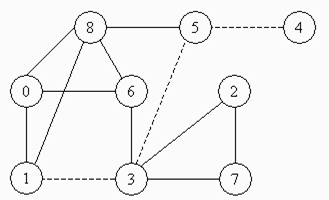Рис.6.5. Діаграма сумісності

Будуємо ПТП (табл. 6.7). Створена ПТП заповнена не повністю, частина кліток залишається вільною, що характеризує відповідні переходи як невизначені або недопустимі. Аналізуючи створену ПТП, бачимо, що в ній відсутні еквівалентні та псевдоеквівалентні внутрішні стани. Сумісними можуть бути стани (0) і (1); (1) і (6); (0) і (8); (2) і (3) і т.п. На основі сумісності станів будується діаграма сумісності по Муру (рис. 6.5), в якій пунктиром зображені зв’язки між станами для автомата Мілі. Аналіз діаграми сумісності дає можливість виділити дві наступні групи множин сумісності:

1. { (0), (1), (8) }, { (2), (3), (7) }, { (4), (5) }, { (6) };

2. { (0), (6), (8) }, { (1), (3) }, { (2), (7) }, { (4), (5) }.

В обох випадках кількість множин дорівнює чотирьом. Це говорить про те, що у скороченій таблиці переходів матимемо чотири внутрішні стани. При цьому синтезований пристрій проектуватиметься як автомат Мілі, і для його реалізації знадобляться два елементи пам’яті.

Якщо ж розглядати пристрій як автомат Мура, тобто не враховувати сумісність, позначену пунктирними лініями, то матимемо такі дві групи множин:

1. { (0), (1), (8) }, { (2), (3), (7) }, { (4) }, { (5) }, { (6) };

2. { (0), (6), (8) }, { (2), (3), (7) }, { (1) }, { (4) }, { (5) }.

В обох випадках мінімальна кількість множин сумісності рівна 5, а для реалізації автомата знадобиться вже три елементи пам’яті.

Скорочена таблиця переходів, побудована на основі першого варіанту об’єднання (при проектування як автомата Мілі) приведена в табл. 6.8.

Таблиця 6.8.

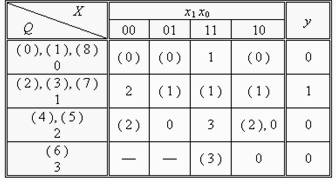
У приведеній таблиці множина { (0), (1), (8) } зображена у вигляді одного стану 0; множина { (2), (3), (7) } – зображена станом 1; множина { (4), (5) } – відповідно, станом 2; множина { (6) } – станом 3.