Векторные диаграммы переменных токов и напряжений

Из курса математики известно, что любую синусоидальную функцию времени, на­пример i(t)=I_msin(wt+a), можно изобразить вращающимся вектором при соблюдении следую­щих условий :

а) длина вектора в масштабе равна амплитуде функции I_m ;

б) начальное положение вектора при t = 0 определяется начальной фа­зой a ;

в) вектор равномерно вращается с угловой скоростью w, равной угло­вой частоте функции.

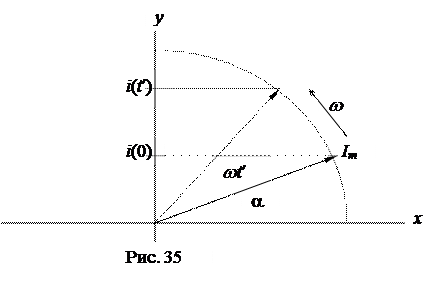При соблюдении названных условий проекция вращающегося вектора на вертикаль­ную ось y в системе координат х-у в любой момент времени t¢равна мгновенному значению функции i(t¢), следовательно i = I_m sin(wt+a)

Рассмотрим процессы в схеме электрической цепи рис. 36. Изобразим си­нусоидаль­ные функции токов и напряжений вращающимися векторами для произвольного момента времени, например t = 0 (рис. 37а). При рассмотрении установившегося режима в схеме мгно­венные значения функций не представ­ляют интереса, поэтому момент времени, для которого строится векторная диа­грамма, может быть выбран произвольно. Целесообразно один из век­торов принять начальным или исходным и совместить его на диаграмме с одной из осей ко­ординат (вектор Е на рис. 37б совмещен с осью y), при этом остальные векторы располагают по отношению к исходному вектору под углами, равными их сдвигам фаз.

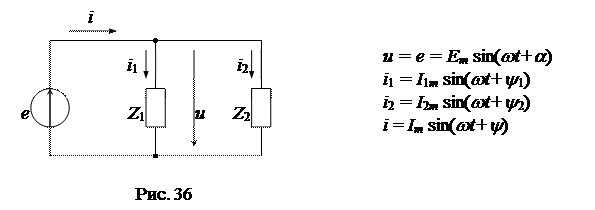
Так как на практике интерес представляют действующие значения токов и напряже­ний, то на векторных диаграммах длины векторов принимают рав­ными в выбранных мас­штабах их действующим значениям (рис. 37б).

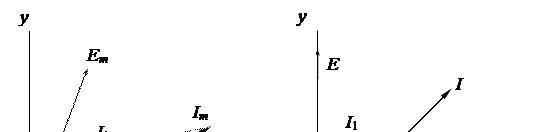Совокупность векторов, характеризующих процессы в цепи перемен­ного тока, по­строенных в выбранных масштабах и с соблюдением правильной их ориентации друг отно­сительно друга, называется векторной диаграммой.