Понятия обратимых и необратимых процессов 5 глава

Ядрышко - сферическая структура, функция которой - синтез рРНК, из которой состоят рибосомы. Транспорт рРНК в цитоплазму происходит через ядерные поры - отверстия в ядерной оболочке, посредством которых осуществляется контакт кариоплазмы с содержимым клетки.

Главными функциями ядра являются:

1) хранение генетической информации и передача ее дочерним клеткам в процессе деления;

2) контроль жизнедеятельности клетки путем определения, какие белки и в каких количествах должны синтезироваться.

4.4. Мембрана клетки как сферический конденсатор

Электрическое сопротивление 1 см мембраны составляет (10²…10⁶) ом, что в десятки миллионов раз больше сопротивления внеклеточной жидкости или цитоплазмы. Электроизоляционные свойства мембран значительно превосходят свойства технических изоляционных материалов. Напряженность электрического поля в мембране E=200·10³ В/м. В обычных диэлектриках пробой происходит при гораздо меньших напряженностях поля.

. Мембрану клетки можно представить в виде сферы. Немембранный слой имеет относительную диэлектрическую проницаемость ε от 2 до 6.

В таком случае емкость мембраны (Ф) можно найти по формуле

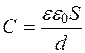, (4.1)

где ε – диэлектрическая проницаемость среды, Ф/м;

ε₀=8,84·10^-12 Ф/м - диэлектрическая проницаемость вакуума;

S – площадь сферы, м²;

d – разность радиусов внешней и внутренней сфер конденсатора, м.

,

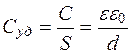откуда

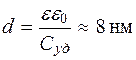. (4.2)

Таким образом, мембраны клетки принимают самое активное участие в ее жизнедеятельности.

Во-первых, вследствие проницаемости происходит перенос (транспорт) веществ в клетку и из нее.

Во-вторых, в клетке локализуются основные биоэлектрические процессы.

В-третьих, в мембранах митохондрий синтезируется АТФ - основной источник энергии в живом организме. Есть предположение, что репликация ДНК и хромосом также происходит с участием мембран.

К основным функциям мембран можно отнести следующие:

1) барьерная — обеспечивает управляемый (селективный), то есть избирательный обмен с окружающей средой;

2) матричная — обеспечивает взаимное расположение и ориентацию мембранных белков;

3) механическая — обеспечивает прочность внутриклеточных структур;

4) энергетическая — мембраны участвуют в синтезе универсальных аккумуляторов энергии АТФ в митохондриях, фотосинтезе и т.д.;

5) генераторная — мембраны участвуют в образовании электрических потенциалов;

6) рецепторная — формирует структуру клетки, осуществляют ее функции – механические, акустические и т.д.;

Многие заболевания связаны с нарушением структуры и функций клеточных мембран.

4.5. Физико-химические методы исследования клеточных мембран

Современное представление о строении биологических мембран связано с использованием физико-химических методов исследования. Большую роль в строении биологических мембран сыграла электронная микроскопия.

4.5.1. Электронная микроскопия

Свет обладает дуализмом. Наряду с электромагнитной теорией, свет представляет собой поток частиц - фотонов. Фотон - элементарная частица, обладающая волновыми свойствами:

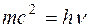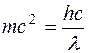; ; , (4.3)

где h=6,63·10^-34 Дж·с - постоянная Планка;

ν- частота светового пучка, с^-1;

λ- длина волны, м.

Де-Бройль Л. предположил, что все частицы обладают волновыми свойствами:

, или . (4.4)

Волновые свойства частиц были использованы для получения увеличенного изображения предмета. Как известно, предел разрешения оптического микроскопа определяется предельным значением длины волны света, воспринимаемого глазом. Для оптического микроскопа

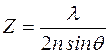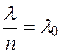; , или 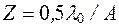, (4.5)

где Z - разрешающая способность микроскопа, то есть способность видеть две ближайшие точки предмета без искажения;

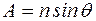- апертура;

n - показатель преломления объектива;

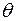-апертурный угол.

Таким образом, световой микроскоп не позволяет рассмотреть детали объекта меньше половины длины волны света, то есть около 200 нм. Следовательно, в оптическом микроскопе можно рассмотреть только отдельные клетки, то есть он совершенно не пригоден для изучения биологических мембран. Оптическая способность Z, как известно, ограничена явлением дифракции. Поэтому, чем меньше длина волны, по сравнению с размерами исследуемого объекта, тем меньше искажение ( ).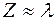

Обратимся к электронному микроскопу. Пусть электрон массой m и зарядом e, вылетающий из электронной пушки со скоростью v, имеет энергию

, (4.6)

отсюда .

Длина волны Де-Бройля будет

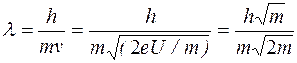, или . (4.7)

Для получения пучка электронов, который можно зафиксировать на экране осциллографа, необходимо U=1 кВ, тогда , что соответствует рентгеновским лучам. Это уже позволяет рассмотреть отдельные детали клеточных мембран. Недостатком электронной микроскопии является деформация объекта в процессе исследования, так как производится обезвоживание, закрепление ультратонких сред и т.д. С помощью электронной микроскопии удалось: 1) получить изображение биологических мембран; 2) рассчитать толщину мембраны.

Было получено трехслойное строение мембраны. Толщина ее, по расчетам многих авторов, 2…3 нм. Значительно изменилось представление о строении мембран. Была отвергнута "бутербродная модель", просуществовавшая более 40 лет. Новая информация о строении биологических мембран была получена с помощью метода, который называется "замораживание-скол-травление" и состоит в следующем:

1) клетку охлаждают до очень низкой температуры в жидком азоте;

2) охлаждение производят с большой скоростью (100 °C в секунду);

3) клетку раскалывают специальным ножом и помещают в вакууме. Лед возгоняется, освобождая поверхность скола (этот процесс называется травлением). После травления получают отпечаток сколотой поверхности;

4) скол фотографируют в электронном микроскопе. Таким образом можно фиксировать внутреннее строение мембраны.

Было доказано, что структурную основу биологической мембраны составляет двойной слой фосфолипидов, который инкрустирован поверхностными и интегральными белками. Молекула фосфолипидов представляет собой цилиндр, 1/3 которого гидрофильна (полярная головка), то есть может притягивать молекулы воды и образовывать водородные связи, 2/3 - гидрофобны. Белки, входящие в состав мембран, также весьма разнообразны. В их состав входит от 100 до 500 аминокислот. Белки занимают 75…80% поверхности мембран. Белковые молекулы покрывают мембрану с обеих сторон, придавая ей эластичность и устойчивость к механическим повреждениям. Как уже говорилось, принято разделять белки на интегральные и периферические. Интегральные белки имеют на поверхности большие гидрофильные участки и располагаются внутри мембран. Периферические находятся на ее поверхности. Доказано, что они могут менять степень погружения в липидный слой и перемещаться в плоскости мембраны (рис. 4.3).

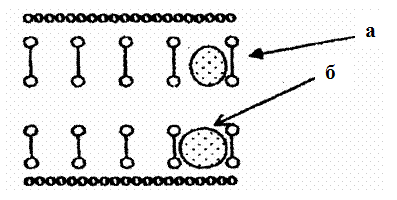
Рис. 4.3. Строение клеточной мембраны: а - интегральные белки; б - периферические белки

В тех местах, где интегральные белки пронизывают бислой, могут образовываться каналы (поры). Диаметр каналов 0,35…0,8 нм. В эритроцитах вся площадь каналов составляет 0,06% от поверхности мембраны. Полярная группа белков в каналах направлена в сторону отверстия канала, а неполярные вступают во взаимодействие с молекулами липидов. Таким образом, стенки каналов обладают электрическими зарядами. Это играет большую роль при прохождении ионов через канал. Разными физическими методами доказано, что длина липидных молекул ≈3 нм (это фиксировали с помощью электронного микроскопа) толщина бислоя 1 нм. Таким образом, толщина всей мембраны ≈ 8…10 нм. На одну молекулу белка приходится 75-90 молекул липидов.

4.5.2. Рентгеноструктурный анализ

Одним из физических методов, широко используемых для изучения строения клеточных мембран, является рентгеноструктурный анализ. Следует отметить, что в настоящее время естествознание пользуется двумя главными способами для изучения строения атома и молекулы. Это химический и оптический анализ. Химический анализ расшифровывает первичную структуру биополимеров, к которым относятся белки. Однако химическим путем нельзя установить пространственных строений белка или нуклеиновых кислот. Рентгенография же дает полную информацию о расположении атомов в молекулах и кристаллах. Рентгеновские лучи (электромагнитные волны λ=0,1 нм) рассеиваются на электронных облаках атомов. Интерференция волн, рассеянных веществом, приводит к возникновению дифракционной картины. Если рассеяние происходит на кристаллах, то дифракцию можно рассматривать как отражение рентгеновских лучей плоскостями кристаллической решетки.

Возбуждение рентгеновских лучей. Рентгеновские лучи возникают при бомбардировке какого-либо вещества быстро двигающимися электронами. В настоящее время рентгеновские лучи получают в специальных электровакуумных приборах – рентгеновских трубках. Рентгеновская трубка представляет собой стеклянный сосуд, из которого эвакуирован воздух (вакуум 10^-5 … 10^-7 мм рт. ст.).

В противоположные концы сосуда впаяны анод и катод. Катод сделан из вольфрамовой проволоки в виде спирали. Спираль накаливается электрическим током и является источником свободных электродов. Анод – массивный медный стержень, обращен­ный своим торцом к катоду. В торец анода впаивается тонкая пла­стинка какого-либо металла, называемая зеркалом анода. Схемы рентгеновской трубки и ее включения для генерирования рентгеновских лучей показаны на рис. 4.4.

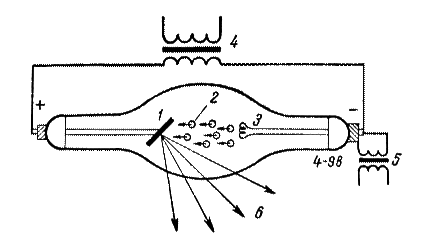
Рис. 4.4. Схема возбуждения рентгеновских лучей:

1 – анод; 2 – электроны; 3 – катод; 4 – высоковольтный трансформатор; 5 – трансформатор накала; 6 – рентгеновские лучи

к электродам трубки, свободные электро­ны, образовавшиеся Под действием электрического поля, образованного напряжением, приложенным на катоде в результате его нагревания, с большой скоростью будут перемещаться к аноду. Наталкиваясь на анод, электроны резко тормозятся, в результате чего и возникают рентгеновские лучи, состоящие из двух компонентов, так называемых тормозного и характеристического излучений.

Тормозной рентгеновский спектр. Скорость движения электрона в рентгеновской трубке, а, следовательно, и его кинетическая энергия определяются разностью потенциалов на участке анод – катод. Встречая на своем пути анод, электрон резко тормозится, его энергия движения переходит в энергию фотона, т. е. кванта лучистой энергии

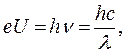(4.8)

где е – заряд электрона;

U – разность потенциалов;

h – постоянная Планка;

с – скорость света;

ν – частота электромагнитного колебания;

λ – длина волн.

Торможение электронов на аноде рентгеновской трубки может происходить по-разному: одни из них тормозятся мгновенно на самой поверхности анода, что соответствует фотону максимальной величины, другие, проникая в глубь анода и постепенно теряя свою энергию, например, на тепло, к моменту торможения будут обладать меньшей энергией.

Следовательно, при торможении электронов возникнут фотоны самой разнообразной энергии, а так как количество их, излучаемое в единицу времени, очень велико, то тормозной спектр будет состоять из непрерывного ряда длин волн с резкой границей в коротковолновой части. Характер распределения энергии в спектре торможения при различных напряжениях показан на рис. 4.5. Тормозное рентгеновское излучение называют сплошным или белым по аналогии с видимым светом.

Характеристический рентгеновский спектр. Из многочисленных исследований рентгеновского излучения было установлено, что, кроме неоднородных лучей торможения, при некоторых условиях возникают однородные лучи, длины волн которых зависят только от материала анода рентгеновской трубки и не зависят от приложенного к трубке напряжения. Этот вид рентгеновского излучения назвали характеристическим.

Рис. 4.5. Распределение интенсивности рентгеновских лучей в сплошном спектре

Характеристический рентгеновский спектр состоит из нескольких групп линий – серий, значительно отличающихся друг от друга по длине волны. Для более тяжелых элементов таких серий было найдено четыре: К, L, М, N (рис. 4.6).

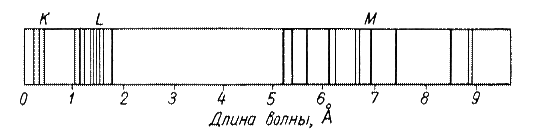
Рис. 4.6. Спектр характеристического рентгеновского излучения

Каждая серия состоит из определенного числа спектральных линий, которые обозначаются буквами греческого алфавита α, β и γ с индексами 1, 2 и т. д. (например, ).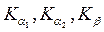

Характеристические спектры различных элементов примерно одинаковы по числу и взаимному расположению линий в сериях и отличаются друг от друга только длиной волны. С увеличением менделеевского числа весь спектр сдвигается в коротковолновую область.

Все линии любой серии возникают одновременно, как только напряжение на электродах рентгеновской трубки (а, следовательно, и энергия электронов) достигает определенной величины для этой серии. Это напряжение называют критическим потенциалом возбуждения данной серии U_k.

Закономерности характеристического спектра позволили создать теорию его возникновения, основанную на квантовой теории строения атома. Так, например, для возбуждения K-серии рентгеновского спектра необходимо удалить электрон с самого внутреннего уровня энергии К на периферию атома (рис. 4.7). Это удаление может быть произведено одним из электронов, бомбардирующих вещество анода рентгеновской трубки. При этом энергия врывающегося электрона должна быть равна или больше энергии связи электрона в слое К со своим ядром.

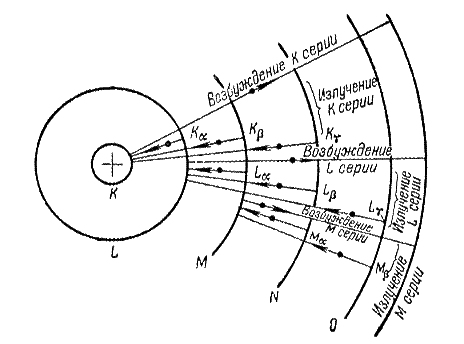
Рис. 4.7. Схема возникновения отдельных серий характеристического рентгеновского излучения

Освободившееся место в K-слое будет тотчас же заполнено за счет одного из электронов верхних слоев, в результате чего выделится рентгеновский фотон, энергия которого численно равна разности энергии уровня, из которого он вышел, и уровня, на который он перешел

hv = E₂ – E₁, (4.9)

где Е₂ — энергия электрона на более удаленной орбите;

Е₁ — энер­гия электрона на более близкой орбите.

Так как описанный выше процесс возбуждения K-серии наблюдается одновременно в громадном количестве атомов, а вероятность перехода электрона из вышерасположенных слоев в K-слой неодинакова, то все спектральные линии серии возникнут одновременно, а их интенсивность (определяемая вероятностью перехо­дов) будет различной.

На рис. 4.7 показана схема возникновения К- и L-серий рентгеновских лучей. В действительности характеристический рентгеновский спектр имеет более сложное строение. Практическое значение в рентгеноструктурном анализе имеют линии К-серии: 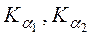и К_β. Анализы проводят на К_α-лучах с длиной волны λ_α, которую определяют как

К_β - лучи поглощаются селективным фильтром. В качестве фильтра берут вещество с порядковым номером на единицу меньше, чем порядковый номер вещества анода рентгеновской трубки. Если анод из кобальта, то фильтр должен быть из фольги железа, если анод из меди, то фильтр – из никеля и т. п. Приблизительное распределение энергии в рентгеновском спектре показано на рис. 4.8. В кристаллическом веществе пространственное расположение атомов и молекул периодично. На известных расстояниях и в определенных направлениях можно встретить химически одинаковые атомы. В качестве схемы строения кристаллического вещества принята пространственная решетка. Пространственную решетку можно представить себе состоящей из бесконечно большого числа совершенно одинаковых параллелепипедов, называемых элементарными ячейками. Форма и размер элементарной ячейки характеризуются шестью константами: длинами ребер а, b, с (период решетки или осевые единицы) и углами между ними α, β, γ (рис. 4.9).

Рис. 4.8. Распределение интенсивности рентгеновских лучей в характеристическом спектре

Для построения простой кубической решетки достаточно знать одну константу а, часто называемую постоянной решетки. Из рис. 4.9 и 4.10, а видно, что постоянная решетки характеризует расстояние между идентичными атомами по осям координат. Существуют и более сложные решетки, в которых частицы вещества расположены не только в вершинах параллелепипедов. Такие решетки можно рассматривать как совокупность нескольких простых решеток, сдвинутых определенным образом одна относительно другой. Так, например, наиболее часто встречаются кубические решетки двух типов, объемноцентрированные и гранецентрированные (элементарные ячейки этих решеток показаны на рис. 4.10, б, в).

Объемноцентрированную решетку можно представить, как две простые решетки, вложенные одна в другую, причем узловые атомы одной из них находятся в центре объема элементарной ячейки другой. Гранецентрированную решетку можно представить как четыре простые решетки, расположенные так, что каждая вершина второй, третьей и четвертой решеток находится в центре граней куба первой решетки.

Рис. 4.9. Пространственная кристаллическая решетка

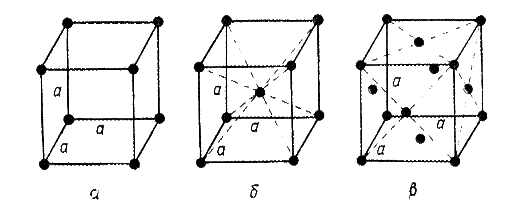
Рис. 4.10. Элементарная ячейка кубической решетки:

а – простая, или примитивная; б – объемноцентрированная; в – а гранецентрированные

Следовательно, количество атомов, приходящихся на одну элементарную ячейку, будет зависеть от типа решетки. На рис. 4.9 и 4.10, а показано, что в простой решетке на одну элементарную ячейку приходится только один атом, так как каждый атом в вершине куба относится одновременно к восьми соседним ячейкам (см. рис. 4.9). Поэтому данной элементарной ячейке будет принадлежать только один атом (или узел), а остальные семь атомов – соответственно семи соседним ячейкам. Тогда в объемноцентрированной и гранецентрированной решетках на одну ячейку будет приходиться соответственно два и четыре атома.

В пространственной решетке через отдельные группы атомов можно провести бесчисленное количество параллельных плоскостей. Совокупность параллельных атомных плоскостей называется семейством атомных плоскостей, а расстояние между ними – межплоскостным расстоянием d (рис. 4.11). Количество атомов, входящих в ту или иную плоскость, различно и тем меньше, чем меньше межплоскостное расстояние.

Положение любой атомной плоскости в пространственной решетке определяется при помощи трех простых целых чисел. Эти числа называются индексами плоскости (индексы Миллера) и представляют собой величины, обратные величинам отрезков, отсекаемых плоскостью на осях координат. Индексы плоскости обозначаются буквами h, k, l и заключаются в скобки.

Преимущества определения положения атомных плоскостей при помощи индексов (h, k, I), а не осевых отрезков, отсекаемых плоскостями на осях координат, будут очевидны, если учесть, что они всегда являются простыми целыми числами и величина их не зависит от внешних влияний (температура, растяжение, сжатие и т. п.), чего не наблюдается у осевых отрезков. Кроме того, индексы (h k I) наиболее просто определяют положение атомных плоскостей в кристаллической решетке.

Рис. 4.11. Различные семейства атомных плоскостей

Постоянная кубической решетки, межплоскостные расстояния и индексы плоскости связаны между собой следующим выражением

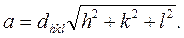(4.10)

Дифракция рентгеновских лучей. Прохождение рентгеновских лучей через кристаллическое вещество сопровождается отклонением их от первоначального направления. Это явление называется дифракцией рентгеновских лучей.

Под действием электромагнитного поля рентгеновских лучей электроны атомов, входящих в кристаллическую решетку вещества, начинают колебаться. Частота вынужденных колебаний электронов будет равна частоте электромагнитного поля первичного пучка рентгеновских лучей. Колеблющийся атом становится источником электромагнитных волн, распространяющихся от него во все стороны с частотой, равной частоте первичного пучка. Расположение атомов в любой кристаллической решетке закономерно и расстояния между ними в данном направлении одинаковы, поэтому лучи, рассеянные отдельными атомами, будут интерферировать между собой. Интенсивность их в одних направлениях будет получаться значительно больше, чем в других. Следовательно, для рентгеновских лучей кристалл является трехмерной дифракцион­ной решеткой.

Уравнение Вулъфа – Брегга. В 1913 г. русский физик Г. В. Вульф дал более простое и наглядное объяснение отклонению рентгеновских лучей при прохождении их через кристаллическое вещество. Он показал, что рассеивание рентгеновских лучей атомами можно рассматривать как отражение рентгеновских лучей от параллельных атомных плоскостей кристалла.

Пусть на кристалл падает пучок монохроматических рентгеновских лучей, образуя угол θ с одним из семейств атомных плоскостей (рис. 4.12, а). Луч S₁, попадая на атомную плоскость P₁,отразится от нее в направлении S. Второй луч S₂, пройдя первую атомную плоскость (на основании свойства рентгеновских лучей проникать через вещество), отразится от плоскости Р₂ и также выйдет в направлении S и т. п. Отраженные параллельными атомными плоскостями лучи будут интерферировать между собой и в зависимости от их фазового соотношения усиливать пли ослаблять друг друга. Отсюда следует, что в направлении S интенсивность рентгеновских лучей будет максимальной, когда лучи, отраженные отдельными атомными плоскостями, будут находиться водной фазе, т. е. когда разность их хода будет кратна длине волны.

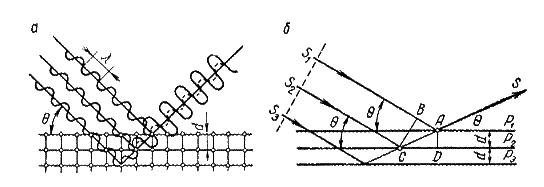
Рис. 4.12. Дифракция рентгеновских лучей

Фазовые соотношения отраженных лучей будут зависеть от длины волны λ, межплоскостного расстояния d и угла скольжения θ (рис. 4.12, а, б). Выразим математически эту зависимость.

В точках В и С лучи S₁ и S₂ находятся в одной фазе (так называемый фронт плоской волны). После отражения луча S₁ вточке А и луча S₂ в точке С оба они пойдут в одном направлении СAS. Луч S₂ пройдет путь, больший, чем луч S₁ на величину АС – АВ, называемую разностью хода. Отражение рентгеновских лучей в направлении СAS будет наблюдаться при разности хода кратной длине волны, т. е. при условии, что АС – АВ = пλ, где п – ряд целых чисел, т. е.

nλ = 2d sinθ. (4.11)

Таким образом, каждое семейство атомных плоскостей будет давать ряд отражений в зависимости от того, какие значения может принимать величина п (1, 2, 3 и т. д.), чтобы sin θ не превышал единицы. Соотношение (4.11), называемое уравнением Вульфа – Брегга, является основным расчетным уравнением рентгеноструктурного и рентгеноспектрального анализа.

При помощи этой формулы, зная межплоскостные расстояния и измерив каким-либо способом углы скольжения, можно вычислить длины волн отраженных рентгеновских лучей (рентгеноспектральный анализ). зная длину волны монохроматических или характеристических рентгеновских лучей и углы скольжения, можно вычислить межплоскостные расстояния (рентгеноструктурный анализ).

Метод Дебая – Шеррера. Первоначально для рентгенографических исследований применяли только крупные, хорошо сформированные одиночные кристаллы изучаемого вещества. Это было очень неудобно, так как не все вещества можно получить в виде крупных монокристаллов. Поэтому стали искать новый более доступный метод рентгенографического исследования. Такой метод, позволяющий выполнять рентгеноструктурные исследования с порошкообразным веществом, был разработан Дебаем и Шеррером.

Пусть некоторое семейство плоскостей в кристалле образует с падающим пучком монохроматических рентгеновских лучей угол θ, удовлетворяющий уравнению Вульфа – Брегга (рис. 4.13). Не меняя угла скольжения (т. е. сохраняя условие Вульфа – Брегга), будем вращать кристалл вокруг оси первичного пучка. Отраженный луч, очевидно, опишет в пространстве конус с углом при вершине, равном 4θ. Другое семейство плоскостей этого же кристалла даст такой же конус, но уже с иным углом при вершине и т. п. Если на пути отраженных лучей перпендикулярно первичному пучку поставить фотопластинку, то на ней зафиксируется ряд концентрических колец по числу семейств атомных плоскостей, отражающих рентгеновские лучи.

Рис. 4.13. Схема образования конусов отраженных лучей:

1 – нормаль к отражающей плоскости; 2 – конус отраженных лучей; 3 – первичный пучок; 4 – отражающая плоскость

При замене монокристалла поликристаллическим веществом из-за беспорядочного расположения отдельных кристаллов всегда найдутся такие, у которых рассматриваемое семейство плоскостей будет удовлетворять уравнению Вульфа – Брегга.

Следовательно, отражения от данного семейства атомных плоскостей каждого кристаллика, находящегося в пучке рентгеновских лучей, будут сливаться в одну сплошную конусную поверхность (конус дифракции), количество таких конусов будет соответствовать количеству семейств атомных плоскостей (рис. 4.14)

Зафиксировать положения дифракционных конусов можно только в случае применения гибкой фотопленки, так как телесный угол, в котором они наблюдаются, равен 360˚ (рис. 4.13 и 4.15). Расстояние между двумя симметричными линиями на пленке зависит от угла при вершине конуса и расстояния пленки от исследуемого вещества.

Рис. 4.14. Образование симметричных линий на рентгенограмме

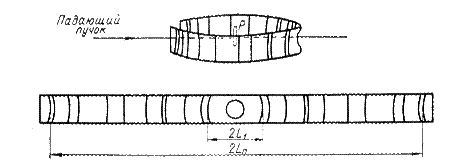
Рис. 4.15. Рентгенограммы поликристаллического вещества

Эти величины связаны между собой следующим образом.

2L = R4θ, (4.12)

где 2L – расстояние между симметричными линиями, измеренное по экваториальной линии на пленке, мм;

R - радиус цилиндри­ческой пленки, мм;

θ - угол скольжения, рад. Или, выражая угол в градусах

Это основная расчетная формула в рентгеноструктурном анализе порошков по методу Дебая – Шеррера. Если известен диаметр цилиндрической пленки и расстояние между симметричными линиями на ней, то определяют углы скольжения. Значения межплоскостных расстояний определяют по уравнению Вульфа – Брегга.