Понятия обратимых и необратимых процессов 2 глава

Рассмотрим следующую формулировку с молекулярно-кинетической точки зрения. Молекулярно-кинетическая теория вещества ставит своей задачей объяснение макроскопических свойств тел, то есть молекулярных процессов, происходящих в телах. Причем значение макроскопических величин мы рассматриваем как средние величины, то есть величины, которые характеризуют рассматриваемый молекулярный процесс, например, среднее значение величины давления газа и т.д. Таким образом, беспорядочность движения молекул ведет к наличию определенных закономерностей. Макроскопические величины – давление, энергия, трение и т.д. – обладают определенным значением, потому что они являются средними значениями очень большого числа отдельных элементарных процессов. В то же время, при наблюдении явлений в малых масштабах, когда число наблюдаемых молекул невелико, должны встречаться отступления от установленных средних значений. Такое отступление называется флуктуацией.

Например, имеем

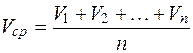. (2.24)

Пусть газ состоит из 4-х молекул. В этом случае может произойти следующее: он вначале расширится, а затем вновь сожмется. Процесс расширения газа в данном случае оказался обратимым. Но обратимость такого процесса маловероятна при значительном количестве молекул. Если считать самопроизвольное расширение газа "положительным", а сжатие его "отрицательным", то можно сделать вывод: отрицательный процесс самопроизвольного сжатия газа весьма маловероятен. Или для всех процессов - необратимый процесс есть такой, обратный которому маловероятен. Это будет вторая формулировка второго начала термодинамики. И наконец, переход работы в теплоту означает то, что в результате действия внешних сил происходит усиление беспорядочного движения молекул. Следовательно, этот процесс сводится к переходу сравнительно упорядоченного движения в беспорядочное. Такой процесс вероятен. Переход теплоты в работу означает переход беспорядочного движения в упорядоченное - такой переход маловероятен.

Таким образом, второе начало термодинамики указывает на необратимость перехода работы в тепло, так как переход тепла в работу означает переход от более вероятного состояния к состоянию маловероятному. Отсюда вытекает третья формулировка: невозможен принцип осуществления такого периодического процесса, единственным результатом которого было бы получение работы за счет взятого количества тепла от одного источника. Или невозможно построить двигатель с КПД=1. Это естественно, так как для осуществления перехода теплоты в обратном направлении нужна работа против внешних сил.

2.5.1. Круговые процессы

Круговым процессом, или циклом, называется такая последовательность превращений, в результате которой система, выведенная из некоторого состояния, вновь в него возвращается. На диаграмме (рис. 2.6) такой процесс изображен замкнутой кривой 1-а-2-b-1. Внутренняя энергия системы в результате цикла не меняется (∆U=0), и первое начало для цикла приобретает вид

Q =А.

При переходе системы из состояния 1 в состояние 2, переходом 1-а-2, объем газа возрастает, работу совершает газ. Работа положительна и равна площади под кривой 1-а-2:

A₁ =S (V₁, l-a-2, V₂)>0.

Эту работу газ совершает за счет теплоты Q₁, которую он получает от окружающей среды (нагревается). Чтобы цикл замкнулся, система переводится из состояния 2 в состояние 1 процессом 2-b-1. Работа равна площади под кривой 2-b-1:

A₂=S (V₂, 2-b-1, V₁)<0.

Рис. 2.6. График кругового процесса

На сжатие газа затрачивается работа, а так как в результате цикла внутренняя энергия системы не изменяется, система должна возвратить в окружающую среду (холодильнику) некоторое количество тепла Q₂. Результирующая работа рассматриваемого цикла будет А=А₁-А₂. Из рис. 2.6 видно, что она равна площади цикла S(l-a-2-b-1). Эта работа положительна и совершается газом против внешних сил за счет теплоты, полученной газом:

A=Q₁-Q₂=Q. (2.25)

В таком цикле, совершаемом по часовой стрелке, всегда часть теплоты, получаемой газом, превращается в работу. Система, которая периодически повторяет цикл, называется машиной. (Все тепловые машины работают по циклам, совершаемым по часовой стрелке.) Рабочим телом чаще всего является водяной пар. В результате каждого цикла часть теплоты, подведенной к рабочему телу, превращается в работу, которая равна площади цикла. После каждого цикла тело возвращается в исходное состояние, с тем же значением внутренней энергии, следовательно, оно не претерпевает никаких изменений и цикл можно повторять многократно. В этом и состоит принцип действия всех тепловых машин (рис. 2.7). Коэффициентом полезного действия тепловой машины условились называть отношение количества теплоты, превращенного машиной в работу, ко всему количеству теплоты, которое машина получила от нагревателя:

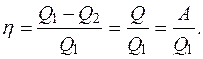(2.26)

В результате каждого цикла машина совершает работу

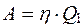. (2.27)

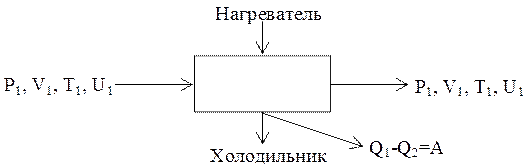
Рис. 2.7. схема действия тепловой машины

Чтобы провести цикл «против часовой стрелки», необходимо затратить работу, равную площади цикла. По циклу «против часовой стрелки» работают холодильные машины.

2.5.2. Цикл Карно

Чтобы проанализировать второе начало термодинамики и придать ему математическую формулировку, рассмотрим обратимый цикл, предложенный Сади Карно в 1824 г. Циклом Карно называется круговой процесс, который состоит из двух изотерм 1-2 и 3-4 и двух адиабат 2-3 и 4-1 (рис. 2.8).

Практически его можно осуществить, если есть один нагреватель и один холодильник. Рабочим телом в цикле Карно является идеальный газ, который находится в цилиндре под поршнем. Стенки цилиндра и поршень не проводят тепло, дно цилиндра изготовлено из вещества, хорошо проводящего тепло. Начальное состояние газа 1 характеризуется параметрами P₁, V₁, T₁.

Из состояния 1 в состояние 2 газ переводится изотермически, параметры состояния 2 — Р₂, V₂, Т₂. Внутренняя энергия в этом процессе не изменяется. Этот процесс произойдет, если от нагревателя, температура которого на бесконечно малую величину выше T₁, газ получит некоторое количество теплоты Q₁ и израсходует ее на работу против внешних сил

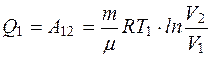. (2.28)

Рис. 2.8. Цикл Карно

Из состояния 2 в состояние 3, с параметрами Р₃, V₃, Т₃, газ переводится адиабатически. При адиабатическом расширении газ охлаждается до температуры Т₂. Для процесса 2-3 выполняется соотношение

. (2.29)

Из состояния 3 в состояние 4, с параметрами P₄, V₄, T₄, газ переводится изотермическим сжатием, на которое затрачивается работа. Эквивалентное количество теплоты Q₂ газ отдает холодильнику, температура которого на бесконечно малую величину ниже температуры газа Т₂.

. (2.30)

Из состояния 4 в начальное состояние 1 газ переводится адиабатическим сжатием, температура газа повышается до начальной T₁. Для адиабаты 4-1 выполняется соотношение

.

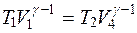Определим КПД этого цикла:

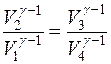; , тогда 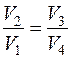и (2.31)

Окончательно

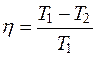. (2.32)

Это выражение получено для обратимого цикла, рабочим телом которого является идеальный газ. Можно показать, что КПД обратимого цикла не зависит от рабочего тела, и все обратимые машины, имеющие одинаковые температуры нагревателей и холодильников, имеют одинаковые КПД.

Можно также доказать, что из всех периодически действующих тепловых машин, имеющих одинаковые температуры нагревателя и холодильника, наибольшим КПД обладают обратимые машины. Выражение (3.32) является количественной формулировкой второго закона термодинамики для простейшего случая, когда имеется один нагреватель и один холодильник, то есть η=1 при Т₂=0.

Но получить температуру, равную абсолютному нулю, невозможно, следовательно, невозможно принципиально построить машину, КПД которой равнялся бы единице (η<1). Пользуясь соотношением (2.32) можно оценить КПД любой реальной машины. Так как реальные машины работают по необратимым циклам, КПД любой реальной машины всегда меньше рассчитанного.

2.5.3. Энтропия

В обратимом цикле Карно идеальный газ получает теплоту при температуре Т₁ и возвращает холодильнику теплоту Q₂ при температуре Т₂ (см. выражения (2.28) и (2.30)).

Поделив 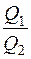, получим 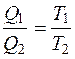, так как 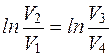, или .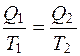

Следовательно, в обратимых процессах поглощается столько Q/T, сколько и выделяется.

Полученное выражение можно переписать в виде

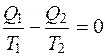. (2.33)

Если после совершения обратного цикла, в результате которого конечное состояние совпадает с начальным, изменение какой-либо величины равно нулю, это значит, что значение рассматриваемой величины не зависит от предшествующих изменений. Величины, отличающиеся подобным свойством, называются функциями состояния. На основании рассмотренного можно утверждать, что существует некоторая физическая величина, изменение которой в обратимом процессе изолированной системы равно нулю (ΔS=0). Следовательно, сама функция остается неизменной (S=const). Функция состояния (S) называется энтропией.

понятие энтропии было дано Клаузиусом в XIX веке. Так как ΔS=0, значит тепло Q₁, поглощаемое при температуре T₁, и тепло Q₂, выделяемое при температуре Т₂, вносят энтропии, равные по величине, но противоположные по знаку, изменения: ΔS₁=Q₁/T₁, ΔS₂=Q₂/T₂ и ΔS₁= –ΔS₂.

Следовательно, изменение энтропии (Дж/град) можно рассчитать по формуле

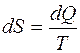, (2.34)

где dQ - количество теплоты, поглощаемой или выделяемой рассматриваемым телом, Дж.

Определим изменение энтропии при переходе системы из состояния 1 в состояние 2 (рис. 2.9).

Чтобы система перешла из состояния 1 в соседнее состояние 1а, бесконечно близкое по значениям параметров, необходимо подвести некоторое количество тепла dQ, при этом энтропия изменится на величину dS.

Изменение энтропии при переходе системы из состояния 1 в состояние 2 получим интегрированием:

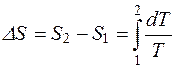. (2.35)

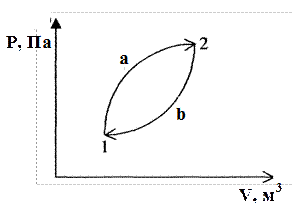
Рис. 2.9. Переход энтропии из одного состояния в другое

Выясним, будет ли изменение энтропии одинаковым при переходе системы из состояния 1 в состояние 2 направлениями 1-а-2 и 1-b-2 Если система переводится из 1 состояния во 2 направлением 1-а-2, а затем возвращается в исходное состояние по другому пути 2-b-1, совершается обратимый цикл, а для обратимого цикла всегда ΔS=0. Следовательно, изменение энтропии на пути 1-а-2 равно изменению энтропии при возвращении системы в исходное состояние направлением 2-b-1. На основании этого можно заключить, что разность (2-1) не зависит от пути перехода системы и определяется только значениями энтропии в точках 1 и 2. Пользуясь формулой (2.35) можно определить изменение энтропии. Например, изменение энтропии при изотермическом расширении газа:

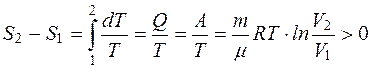. (2.36)

S₁>S₂, следовательно, в этом процессе энтропия возрастает. Пользуясь формулой (2.36) невозможно определить абсолютное значение энтропии, например S₁ и S₂. Неопределенность в значении энтропии устраняется теоремой Нернста, иногда ее называют третьим началом термодинамики. Согласно этой теореме энтропия любого тела при абсолютном нуле равна нулю (Т=0, S=0).

При абсолютном нуле хаотическое движение молекул прекращается и энтропия такого состояния равна нулю. Тогда энтропия в состоянии с температурой Т может быть рассчитана по формуле

. (2.37)

Сообщение телу тепла приводит к усилению теплового движения молекул, то есть к увеличению хаотичности их распределения. На основании этого можно считать, что энтропия определяет беспорядок в системе.

Рассмотрим явление теплопроводности. Это реальный необратимый процесс. Выясним, как изменяется энтропия при переходе системы из неравновесного состояния в равновесное. Пусть горячий камень с температурой Т₁ опускается в холодную воду, температура которой Т₂. Камень отдает воде некоторое количество теплоты ΔQ при температуре Т₁, и энтропия камня уменьшается на величину dQ/T₁. Вода получает это количество теплоты при температуре Т₂, нагревается, и энтропия воды увеличивается на величину dQ/Т₂. Увеличение энтропии системы «камень-вода»:

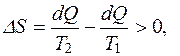так как 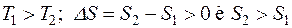. (2.38)

Энтропия системы возрастает. В равновесном состоянии температура системы «камень-вода» становится некоторой Т_ср и энтропия остается постоянной. На основании этого можно заключить, что при переходе системы из неравновесного состояния в равновесное, энтропия системы возрастает и в равновесном состоянии она достигает наибольшего значения. Это положение называется законом возрастания энтропии и является также одним из определений второго начала термодинамики.

Чтобы выяснить физический смысл энтропии, рассмотрим следующий опыт. В цилиндре под поршнем находится газ, его температура Т, тогда внутренняя энергия будет

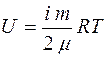. (2.39)

Молекулы газа совершают хаотическое движение, некоторые из них движутся к поршню, и при столкновении с ним эти молекулы передают поршню свою энергию, чем могут переместить его на некоторое расстояние. Следовательно, газ может совершить работу за счет своей внутренней энергии. Чтобы вся внутренняя энергия газа превратилась в работу, необходимо, чтобы все молекулы газа двигались к поршню и, столкнувшись с ним, передали ему всю свою энергию. Но превратить хаотическое движение молекул в полностью упорядоченное невозможно, а значит невозможно всю внутреннюю энергию превратить в работу. Часть внутренней энергии, которая при данных условиях может быть получена в виде тепла и не может быть превращена в работу, называется связанной энергией. Она определяется значением энтропии при данной температуре и равна TS.

Часть внутренней энергии, которая в изотермическом процессе может быть частично или полностью превращена в работу, называется свободной энергией (F). Следовательно, внутренняя энергия состоит из свободной и связанной энергий: U=F+TS. На основании изложенного можно считать, что энтропия является мерой обесцененности внутренней энергии системы. Чем больше энтропия, тем менее ценна энергия в смысле превращения ее в работу. Для пояснения рассмотрим следующий пример. Если имеется пар при температуре 150 °С и давлении, немного большем атмосферного, его можно выпустить в сосуд с холодной водой; пар полностью сконденсируется и вода немного нагреется. До смешения пара с водой пар мог в тепловой машине совершить некоторую работу. После смешивания с водой практически никакой работы от смеси воды и пара получить нельзя.

Согласно закону сохранения, процесс смешивания не вызвал никакого изменения количества энергии, но после смешивания мы потеряли возможность получить работу. Это свидетельствует о том, что процесс смешивания привел не только к выравниванию температуры, но и к потере возможности превращения тепла в работу, то есть качество энергии ухудшилось - энергия обесценилась. Подобная обесцененность энергии сопровождает любой реальный процесс. Следовательно, энтропия остается постоянной или возрастает только в изолированных системах. В неизолированных системах энтропия может и увеличиваться, и уменьшаться. Поведение энтропии в таких системах не является показателем направления самопроизвольных процессов.

2.6. Статистическое содержание второго начала термодинамики

Посмотрим, как объясняется и формулируется второе начало термодинамики с точки зрения молекулярного строения вещества. Первое начало термодинамики - это частный случай закона сохранения энергии, который является абсолютным законом и выполняется одинаково строго и для отдельных молекул, и для больших объемов, то есть выполняется без ограничений.

Второе начало термодинамики, как физическая закономерность, существенно отличается от первого. Остановимся на этом. В термодинамике мы говорим об определенных состояниях вещества и каждое состояние характеризуется макропараметрами Р и Т. Множество случайных столкновений молекул газа со стенками сосуда, в котором содержится газ, определяет давление, и его можно измерить прибором.

Температура определяется интенсивностью хаотического движения молекул. При Т=const между молекулами газа ежесекундно происходит множество случайных столкновений, и в результате каждого столкновения кинетическая энергия столкнувшихся молекул изменяется.

Если температура газа в разных частях объема разная, тогда в результате случайных столкновений и перемещений отдельных молекул происходит перенос теплоты от одних частей объема к другим.

Если концентрация молекул в разных частях объема разная, тогда в результате случайных столкновений перемещение вещества происходит от места с большей концентрацией к местам с меньшей концентрацией. Следовательно, несмотря на случайный характер отдельных событий в системе наблюдается определенная закономерность: в определенном направлении переносится теплота, вещество и т.д. Законы, которым подчиняются совокупности случайных событий, называются статистическими законами. На основании изложенного можно заключить, что второе начало является статистическим законом, который проявляется в результате случайных перемещений множества молекул. В математике случайные события характеризуются определенной вероятностью. Рассмотрим, что такое математическая вероятность, на примере процесса, протекающего в газах.

Пусть первоначально газ находится в одной из половин сосуда, разделенного перегородкой на две равные части. Если перегородку убрать, газ распространится равномерно по всему объему. Обратный переход газа в одну из половин сосуда без постороннего вмешательства не наблюдается. Посмотрим, почему это не происходит. Одна замеченная молекула одинаково часто попадает во все места объема, то есть в среднем она проводит одинаковое время в обеих частях сосуда. Тогда вероятность того, что в данный момент времени молекула находится в одной половине сосуда, равна 1/2. Так как молекулы идеального газа движутся независимо друг от друга, то вероятность для двух молекул одновременно равна произведению их вероятностей:

.

Следовательно, вероятность того, что моль газа самопроизвольно займет половину первоначального объема, ничтожно малая величина, то есть такое событие может произойти, но чрезвычайно редко. Итак, применив к процессам, происходящим в газе, молекулярно-кинетический метод, удалось установить, что второе начало не является категорическим законом. Процессы, запрещенные вторым началом термодинамики, в действительности оказываются не невозможными, а маловероятными. Газ может самопроизвольно занять половину предоставленного ему объема, но вероятность второго события настолько мала, что она практически не наблюдается.

В термодинамике принято пользоваться не математической вероятностью, а термодинамической. Использование термодинамической вероятности связано с понятиями микро- и макросостояний системы. Одно и то же макросостояние системы, например, одна и та же температура газа может создаваться разным распределением энергии между отдельными молекулами. Число микросостояний, с помощью которых может быть осуществлено данное макросостояние, называется термодинамической вероятностью.

Л. Больцман установил соотношение, связывающее энтропию и термодинамическую вероятность W:

S=k·lnW+const. (2.40)

Энтропия данного состояния системы пропорциональна термодинамической вероятности этого состояния. Все остальные процессы представляют переход системы из менее вероятного состояния в более вероятное. В этом и состоит статистический смысл второго начала термодинамики. Второе начало выполняется тем строже, чем большее число частиц содержится в рассматриваемом объеме. Отступления от второго начала наблюдаются, если в сосуде содержится мало молекул, например: всего четыре, в верхней и нижней части объема по две. Это равновесное состояние системы - результат хаотического движения молекулы, которая из нижней части объема может перейти в верхнюю, то есть система самопроизвольно переходит из равновесного состояния в неравновесное. Происходит процесс, запрещенный вторым началом термодинамики. Самопроизвольные отклонения от средних значений наблюдаются не только для плотности, но и для температуры, давления и других физических величин. Эти отклонения называются флуктуацией данной величины. Флуктуации сказываются во многих явлениях. Например, синий цвет неба объясняется рассеянием света на флуктуациях плотности воздуха в верхних слоях атмосферы. Флуктуации плотности сильно проявляются в веществе вблизи критических точек, например: при критической температуре, при переходе вещества из газообразной фазы в жидкую. На флуктуациях плотности происходит сильное рассеяние света, и вещество становится непрозрачным. Это явление называется критической опалесценцией. Понятие энтропии было введено для изолированных систем, в которых необратимые процессы протекают в направлении увеличения энтропии системы.

2.7. Термодинамические потенциалы

Особые функции, которые используются для практического решения различного рода термодинамических задач, называются термодинамическими потенциалами. Например, подставив выражение (3.36) прироста энтропии в формулу первого начала термодинамики (3.6), получим

dQ=dU+dA=TdS,

отсюда

dU=TdS-dA=TdS-pdV. (2.41)

Выражение dU=TdS-pdV представляет полный дифференциал внутренней энергии.

Вторым термодинамическим потенциалом является энергия Гельмгольца, или, как ее часто называют, свободная энергия:

F=U-TS. (2.42)

Свободной называется энергия, идущая на совершение работы. Связанная энергия - это энергия, идущая на рассеяние в виде тепла. Найдем полный дифференциал dF=dU-TdS-SdT, или, используя полный дифференциал, получим:

dF=-SdT-pdV.

Пусть T=const, dT=0, тогда dF=-pdV=dA.

То есть уменьшение свободной энергии равно работе, совершаемой системой в изотермическом процессе. Так как теплокровные организмы сохраняют неизменную температуру, можно считать, что совершаемая ими работа осуществляется за счет уменьшения свободной энергии. Третий потенциал - потенциал Гиббса будет

G=F+pV; (2.43)

dG=-SdT+Vdp. (2.44)

Пусть система приходит к равновесному состоянию в необратимом изобарно-изотермическом процессе. В этом случае dQ<TdS, и для дифференциала энергии Гиббса вместо равенства получим следующее неравенство:

dG<-Sdt+Vdp;

так как dT=0 и dP=0, то получим

dG<0. (2.45)

Следовательно, наблюдается уменьшение энергии Гиббса, которое будет происходить до тех пор, пока не установится равновесное состояние. Если энергию Гиббса считать равной нулю, то dG=0. Таким образом, в изобарно-изотермическом неравновесном процессе энергия Гиббса убывает, и в состоянии термодинамического равновесия она минимальна. В химической термодинамике, кроме изменения внутренней энергии системы, обусловленной теплообменом и совершенной работой, учитывают изменение числа частиц в системе. Тогда полный дифференциал внутренней энергии системы запишется выражением

dU=TdS-pdV+μdN, (2.46)

где dN - изменение числа частиц в системе;

μ - коэффициент, называемый химическим потенциалом.

Тогда потенциал Гельмгольца и энергия Гиббса будут иметь вид:

dF=-SdT-pdV+μdV и dG=-SdT+Vdp+μdN. (2.47)

Химический потенциал не является термодинамическим потенциалом, а, аналогично давлению, температуре и энтропии, называется параметром системы. Как всякий параметр, он является функцией других параметров.

Если частицы являются заряженными, а система находится в электрическом поле, то вместо химического потенциала используют электрохимический потенциал, который также имеет энергетический смысл:

, (2.48)

где dμ_i - электрохимический потенциал.

Первое слагаемое представляет работу, которую надо совершить, чтобы вызвать химические изменения одного моля компонента при переходе из одного состояния в другое; второе слагаемое - работа одного моля, которая совершается при изменении молярной концентрации, то есть

.

Третье слагаемое соответствует работе, совершаемой против сил электрического поля при изменении состояния одного моля ионов.

2.8. Открытые термодинамические системы. Уравнения Пригожина. Стационарные состояния открытой системы

Сущность второго начала термодинамики для изолированных систем заключается в том, что все необратимые процессы в этих системах протекают в таком направлении, при котором полная энтропия системы увеличивается. Любой организм – открытая система животного или растительного происхождения – не может быть изолирован от окружающей среды. Он поглощает из нее питательные вещества и выводит продукты метаболизма. Исследования последних десятилетий показали, что невозможно изолировать живой организм от внешней среды. И это надо понимать в более широком смысле.

Итак, полеты человека и животных в космос в условиях невесомости показали влияние гравитационного поля на динамику кальциевого обмена в костных тканях. Животные, изолированные от внешнего магнитного поля, болеют и погибают. Другим отличием термодинамики живого организма от классической термодинамики для изолированных систем является тот факт, что последняя рассматривает процессы, находящиеся в состоянии равновесия или близком к нему. Если в изолированной системе (газе или растворе) имеются градиенты (давление, концентрация, температура), то рано иди поздно произойдет их выравнивание, и энтропия достигнет максимума. Другое дело в биологических объектах - открытых системах. Основное свойство живых клеток и тканей — это способность совершать работу за счет изменения энергии соответствующих систем. Так, работа, совершаемая при перемещении веществ через клеточные мембраны, определяется непрерывностью электрического поля, то есть градиентом потенциала Ф по разные стороны мембраны

Работа, совершаемая биологической системой, а следовательно, ее свободная энергия определяются градиентами различной величины, которые, в конечном итоге, обусловлены неравновесным распределением вещества и непрерывным его переносом из одной части системы в другую. В замкнутых системах все самопроизвольные процессы идут в направлении уменьшения свободной энергии и увеличения энтропии. В живых же системах в течение всей жизни поддерживаются температурные, концентрационные, электрические градиенты, и выравнивание этих градиентов означает гибель организма. Таким образом, в открытых системах, вследствие протекания в них биохимических и биофизических процессов, наблюдается изменение свободной энергии и энтропии, которые обусловлены взаимодействием с окружающей средой. Так как все биохимические и биофизические процессы в организме являются необратимыми - протекающими с рассеиванием частиц и переходом энергии в тепло, то в результате этого свободная энергия системы непрерывно уменьшается, а энтропия возрастает.

dF_i<0, dS≥0. (2.49)