Молекулярная структура твердых тел, полимеров и жидких кристаллов
Все твердые тела делятся на кристаллические и аморфные. Вещество, у которого частицы располагаются в строго определенном порядке, характерном для данного вещества, называются кристаллическими. Особенностью кристаллических тел является анизотропия, то есть зависимость физических свойств от направления, в котором эти явления наблюдаются. Одни кристаллы обладают различной механической прочностью, другие по разным направлениям имеют отличия в оптических свойствах и т.п. Большинство веществ в природе имеют кристаллическое строение. Аморфные тела изотропны, то есть физические свойства данных тел по всем направлениям одинаковы (валидол и т.д.).
Различие между кристаллическими и аморфными телами отчетливо проявляется при плавлении. Кристаллические вещества имеют температуру плавления, которая считается постоянной при нагревании вещества. В данном случае тепловая энергия идет на разрушение кристаллической решетки. Таким образом, температурой плавления называется температура, при которой твердая фаза находится в динамическом равновесии с энергией плавления. При кристаллизации выделяется такое же количество теплоты, которое было поглощено при плавлении. Температура расплава повышается до температуры плавления.
При нагревании аморфного вещества его температура все время повышается. Происходит размягчение вещества. Уменьшается его вязкость. Вещество постепенно из твердого превращается в жидкое. Определенных температур плавления у аморфных тел нет. При охлаждении аморфные тела постепенно затвердевают. Увеличивается их вязкость. Поэтому аморфные вещества называют переохлажденными жидкостями.
Обратимся к кристаллам. В зависимости от природы вещества, его кристаллической решетки, кристаллы делятся на атомные, ионные, металлические и молекулярные.
Для оценки параметров кристаллических решеток, для изучения их молекулярной структуры используется метод электронографии и рентгеноструктурного анализа. На основании этих методов было доказано, что простые элементарные вещества имеют атомную решетку. Молекулярные силы в них образуются в результате обмена электронами и образования между атомами общих электронных оболочек.
Два электрона от разных атомов с противоположно направленными силами спариваются на одной орбите и связывают ядра этих атомов силой притяжения. Между атомами образуется обменная, или ковалентная, связь, которая характеризуется высокой прочностью. Такая связь характерна для органических веществ. Как правило, вещества с ковалентной связью атомов отличаются твердостью, высокой температурой плавления и малой растворимостью. К таким веществам относятся ряд активных фармакологических веществ: стрептоцид, кристаллический пенициллин и т.д.
В веществах с ионным строением каждый ион связан с окружающими его ионами противоположного знака силами электростатического притяжения. Вещества с таким строением тверды, хрупки, имеют высокую температуру плавления и хорошо растворимы в воде. Примером может служить поваренная соль с кубической пространственной решеткой.
В металлах пространственная решетка состоит из атомов, потерявших наибольшее число связанных с ядром внешних электронов, то есть состоит из ионов. Оторвавшиеся электроны называются свободными и образуют «электронный газ». Наличие в металлах свободных электронов обусловливает их высокую тепло- и электропроводность.
Взаимосвязь между молекулами и ионами образуется вследствие действия сил Ван-Дер-Ваальса. Это наиболее универсальные в природе силы, которые встречаются не только у твердых тел, но и у жидкостей органической природы.
Биологические жидкости животных и человека по своей молекулярной структуре близки к жидким кристаллам. Жидкими кристаллами называются вещества, которые обладают свойствами жидкостей и кристаллов. По своим механическим свойствам эти вещества похожи на жидкости, так как обладают свойствам текучести. По оптическим свойствам жидкие кристаллы ведут себя как анизотропные вещества - кристаллы. Они вращают плоскость поляризации, обнаруживают двойное лучепреломление. Чаще всего жидкокристаллические свойства жидкие кристаллы проявляют в определенном температурном интервале, выше которого они находятся в аморфно-жидком состоянии, а ниже - в твердокристаллическом.
По молекулярной упорядоченности кристаллы делятся на нематические и смектические. В первых молекулы ориентированы параллельно, а центры расположены беспорядочно, а во вторых молекулы располагаются параллельными упорядоченными слоями. Особый класс составляют кристаллы холестерического типа. Молекулы у таких кристаллов, как и в смектических, собраны в слои. Однако внутри каждого слоя параллельное расположение осей молекул напоминает нематическое состояние.
Молекулярная структура холестерических жидких кристаллов очень чувствительна к любому внешнему воздействию. Малое возмущение может нарушить слабые межмолекулярные силы, что приводит к заметному изменению оптических свойств. В медицине это позволяет фиксировать расположение вен, артерий и других образований, имеющих иную теплоотдачу, чем у окружающей среды. Исследование жидких кристаллов в живых организмах - сверхактуальная перспективная область, так как структура гемоглобина, а также ряда других органических веществ, очень схожа с молекулярным строением жидких кристаллов.
В настоящее время в медицине получили широкое применение полимеры. Полимерами называются высокомолекулярные соединения, состоящие из цепочечного соединения молекул, длина которых достигает нескольких микрон.
Молекулы полимеров состоят из большого числа (до десятка тысяч) одинаковых звеньев, мономеров, представляющих группу из небольшого числа атомов. Полимеры получаются с помощью полимеризации или поликонденсации. К полимерам можно отнести многие органические вещества - крахмал, клетчатка, белок, каучук и другие, а также искусственные - полиэтилен, полистирол, плексиглас и др.
При обычной температуре полимеры могут являться твердыми телами или жидкостями. Твердые полимеры могут иметь как кристаллическое, так и аморфное строение. Они имеют исключительно благоприятные механические свойства (прочность и эластичность), которые связаны с их строением.
Полимеры легко обрабатываются путем давления (спрессовывания). Они применяются для изготовления медицинских инструментов, протезов кровеносных сосудов, клапанов сердца и т.д. Жидкие полимеры используются в качестве заменителя плазмы.
1.2. Механические свойства мышц и костного аппарата. Закон Фанга
Упругие свойства твердых тел подчиняются закону Гука. Вследствие действия внешних сил на твердое тело происходит его деформация, которая при прекращении действия сил полностью исчезает, и тело восстанавливает свой объем и форму. Деформация измеряется относительной деформацией 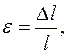 где
где 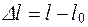 (м), а также напряжением
(м), а также напряжением 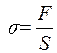 , то есть отношением величины действующей силы F(Н) на площадь сечения тела S(м2).
, то есть отношением величины действующей силы F(Н) на площадь сечения тела S(м2).
По закону Гука относительная деформация пропорциональна напряжению:
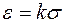 , или
, или 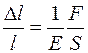 , (1.1)
, (1.1)
где E - модуль Юнга,
Модуль Юнга - это такое напряжение, при котором стержень удлиняется вдвое от своей первоначальной длины l0.
Пусть ε = 1, тогда σ = ε. При этом Δl/l0=1, а 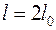 . (1.2)
. (1.2)
Наибольшее напряжение, при котором деформация сохраняет упругий характер, называется пределом упругости. При увеличении напряжения выше предела упругости деформация нарастает и имеет пластический характер. Пластической, или остаточной, деформацией называется деформация, которая сохраняется после прекращения действия всех внешних сил. На графике (рис.1.1) ее участок (ab) показывает предел прочности. Вещества с высоким пределом прочности называются упругими. Тела с большими упругими деформациями, но с малым модулем упругости называются эластичными (каучук). Тела, имеющие узкие пределы упругих деформаций, называются хрупкими. Свойство веществ сопротивляться деформации любого вида называется твердостью.
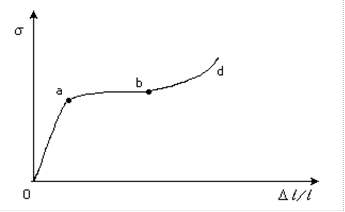
Рис. 1.1. Зависимость напряжения от относительного удлинения: точка а – предел упругости; точка b – предел прочности
При механических нагрузках действуют в основном силы сжатия (например, для позвоночного столба, нижних конечностей и т.д.), растяжения (верхние конечности, связки, сухожилия и мышцы) и изгиба (позвоночник, кости таза, кости конечностей т.п.).
Механические движения животных и человека на протяжении жизнедеятельности осуществляются мышцами. Кровообращение, дыхание и прочие биологически активные акты возможны благодаря наличию в организме мышц. По своим механическим свойствам мышцы относятся к эластомерам, то есть материалам, обладающим эластичностью и упругостью. Они не подчиняются закону Гука. Мышца обладает способностью активного сокращения под действием нервных импульсов, а также под действием внешних раздражений.
Сократительными элементами в мышечном волокне являются микрофибриллы. Мышца представляет собой сложную физико-химическую систему, в которой химическая энергия превращается в механическую работу и теплоту.
Теплопродукция в мышцах обеспечивает значительную часть всей теплоты, продуцируемой в организме. Источником теплопродукции при мышечном сокращении являются биохимические реакции, протекающие с расщеплением микроэнергетических связей в молекулах аденозинтрифосфорной кислоты (АТФ) и фосфоркреатина (ФК).
При сильном, значительном сокращении мышц наблюдается локальная кристаллизация. Это явление было изучено методом рентгеноструктурного анализа. В процессе кристаллизации наблюдается нагревание мышцы. Исследования показывают, что по своим механическим свойствам мышцы приближаются к каучуку. Модуль Юнга приблизительно равен 10-3 кг·с/м2 .
При прекращении деформации мышца восстанавливает свою форму. Однако при значительных деформациях восстановление не бывает полным. Наличие остаточной деформации характеризует пластичность мышцы. Таким образом, исследования показывают, что мышцы не являются абсолютно упругим телом. Они обладают вязкоупругими свойствами.
Мышечные сокращения делятся на изометрические, то есть при неизменной длине мышц происходит сокращение, и изотонические - сокращение происходит при неизменном напряжении.
В зависимости от величины силы, которую преодолевает мышца, скорость сокращения (укорочения) мышцы бывает различной.
Согласно А. Хиллу, скорость сокращения мышцы находится в гиперболической зависимости (Закон Хилла), как это показано на рис. 1.2.
Закон Хилла характеризует зависимость скорости ускорения мышцы от нагрузки, т. е. 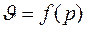
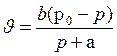 , (1.3)
, (1.3)

Рис. 1.2. Зависимость максимальной скорости сокращения мышц от нагрузки
где p0 – максимальное изометрическое напряжение, развиваемое мышцей, или максимальный груз, который удерживается мышцей без её удлинения;
b – постоянная величина имеющая размерность скорости;
a – постоянная величина имеющая размерность силы;
При p=0 получим значение максимальной скорости
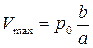 (1.4)
(1.4)
Работа мышцы при одиночном ускорении при величине Δl равна:
A=p·Δl (1.5)
Так как
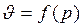 , (1.6)
, (1.6)
то данная величина на является линейной.
Однако если V – const, тогда 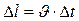 , а развиваемая мышцей мощность
, а развиваемая мышцей мощность 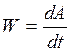 , будет иметь вид:
, будет иметь вид:
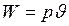 . (1.7)
. (1.7)
Подставляя уравнение Хилла в данную формулу получим:
 (1.8)
(1.8)
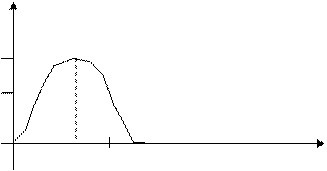
Функция W(p) (зависимость мощности мышцы от нагрузки), графически будет иметь колоколообразную форму (рис. 1.3.)
Данная кривая хорошо согласуется с результатами опытов.
Мощность равна нулю при p=p0 и p=0 и достигает максимального значения при оптимальной нагрузке, т. е.
p=0,31p0 (1.9)
 W/Wmax
W/Wmax
0,5
P/p0
0,31 0,5
Рис. 1.3. зависимость мощности мышцы от нагрузки
Эффективность работы мышцы при сокращении может быть определена как отношение совершенной работы к затраченной энергии:
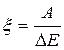 (1.10)
(1.10)
Развитие наибольшей мощности и эффективности сокращения достигается при усилии 0,3…0,4 от максимальной изометрической нагрузки p0 для данной мышцы. Так при подъеме в гору на велосипеде включают низкую передачу, тем самым уменьшают p, приближая ее к p0.
Теория упругости поведения биологических тканей была создана Г. Фангом (1954 г.). Он показал, что деформация биологических тканей имеет нелинейный характер, и напряжение и растяжения связаны соотношением
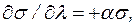 (1.11)
(1.11)
где 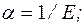
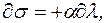
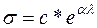
После подстановки начальных условий закон Фанга трансформировали и используют в настоящее время в двух основных формах:
 (1.12)
(1.12)
или 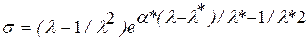 , (1.13)
, (1.13)
где σ* и λ* - начальные условия деформации.
Справедливость этих функций показана на широком классе биологических тканей – портняжная мышца, сосудистая стенка, костная мозоль, кожа человека.
Рассмотрим биофизику мышечного сокращения.
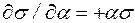 ;
; 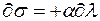 ;
;  ,
,
где l - растяжение мышцы;
с – постоянная величина, характеризующая начальные условия.
Проблема мышечного сокращения заключается в том, что наблюдается прямое превращение химической энергии в механическую при сокращении мышц. При растяжении мышц наблюдается локальная кристаллизация упорядочения макромолекулярной белковой структуры фитриллирного типа. При этом повышается температура. При увеличении в 600 000 раз на микрофотографиях продольного среза мышцы можно увидеть, что последние состоят из миозиновых тканей, которые соединены поперечными мостиками, обеспечивающих структурную целостность мышц. Мышца образована отростками миозиновых тканей, расположенных в интервале 6…7 нм.
В центральной части миозиновых протофибрилл мостики отсутствуют. Этим участкам соответствует «псевдо-Н-зона», обладающая низкой оптической плотностью.
В. Энгельгартом и М. Любимовой (1965) было сделано открытие: миозин обладает ферментативными свойствами, являясь ферментом аденозинтрифосфатазой, которая расщепляет АТФ. В миофибриллах через поперечные мостики миозин образует комплексное соединение с актином.
Энергия, которая выделяется в процессе гидролиза АТФ, используется для сокращения актомиозинового комплекса. Ферментативная активность актомиозина примерно в 10 раз выше активности одного миозина. Ферментативная активность и способность к сокращению актомиозинового комплекса зависит от присутствия ионов кальция. Многие считают, что при отсутствии кальция АТФ вообще не расщепляется. Согласно современным представлениям в клетках функционирует кальциевый насос, работа которого вызывает сокращение миофибрилл. Полагают, что этот насос локализован в мембранах саркоплазматического ретикулума мышечного волокна.
По специальным поперечным трубочкам саркоплазматического ретикулума возбуждение в виде волны деполяризации передается от поверхности волокна, возбуждаемой нервным импульсом, к миофибриллам. Это подтверждается классическим опытом А.Ф. Хаксли с локальным раздражением мышечного волокна лягушки. Им было доказано, что основную роль при мышечном сокращении играют ионы натрия, кальция и магния. Деполяризация трубочек и пузырьков саркоплазматического ретикулума приводит к освобождению ионов кальция, что приводит к проявлению АТФ активности актомиозина и сокращению миофибрилл. Процесс расслабления миофибрилл связан с удалением ионов кальция из саркоплазмы. Элементы ретикулума обладают способностью к активному поглощению ионов кальция из окружающего раствора.
Необходимо отметить, что расслабление миофибрилл при удалении ионов кальция из саркоплазмы происходит только в том случае, если в саркоплазме содержится АТФ.
Удаление АТФ из саркоплазмы приводит к возникновению между актином и миозином сильных электростатических связей, что обусловливает окоченение мышцы и потерю ею способности к растяжению.
Восстановление первоначальной длины мышцы обусловлено, вероятно, наличием упругих элементов в мышечных волокнах и работой мышц. Упругим элементом мышечного волокна является коллагеновая оболочка.
Следует отметить, что большинство гипотез о сокращении мышц сходятся в том, что в основе мышечного сокращения лежат определенные свойства молекулярных цепей сократительных белков, то есть лежат процессы изменений структуры белковых цепей.
Согласно другому представлению акт сокращения представляет собой конформационный переход белковой структуры от α–конфигурации, когда нити линейно вытянуты, к β-конфигурации, когда нити собраны в клубок.
Однако эта гипотеза не смогла объяснить реальную картину сложного строения мышечного волокна на молекулярном уровне, полученную в последнее время.
На основе изучения электронно-микроскопических фотографий, А.Ф. Хаксли выдвинул теорию скольжения нитей. Им было отмечено, что при сокращении и растяжении миофибрилл их ширина остается постоянной; а в большой области деформаций мышцы длина миозиновых и актиновых нитей остается постоянной. Это можно объяснить только тем, что при сокращении мышцы нити просто скользят друг относительно друга без изменения своей длины, вдвигаясь одна в другую.
Весь процесс сокращения нитей имеет циклический характер. Миозиновые мостики прикрепляются к активным участкам нитей, и под действием энергии гидролиза АТФ укорачиваются или изменяют угол наклона к миозиновой нити, что приводит к определенному перемещению нитей друг относительно друга. Затем происходит отсоединение мостиков в данных участках актиновых нитей и присоединение их в новых участках.
Этот циклический процесс повторяется многократно, в результате чего происходит непрерывное перемещение нитей друг относительно друга. Рентгеноструктурный анализ подтвердил это предположение. В дальнейшем с данной позиции было составлено уравнение сокращения мышцы и произведен математический анализ их сокращения. Составленные уравнения выходят за рамки данного курса.
Деформация кости. Костная ткань - это типичный образец композиционного материала, который имеет волокнистую коллагеновую матрицу с минеральными компонентами - кристаллами гидроксилапатита (65-70%).
Упруговязкие характеристики костной ткани изучались в широком диапазоне скоростей деформации (от 0,001 до 15000 с-1).
Было выявлено, что гуковские свойства костной ткани проявляются при высоких скоростях деформации. Разрушение костной ткани наступает в районе напряжений 150 МПа. По мере уменьшения скорости деформации уменьшается модуль Юнга. В области скоростей деформации меньше 0,1 с-1 наблюдается пластическое поведение кости. Экспериментально установлен реологический закон поведения кости:
σ=Аlnε+В, (1.14)
где σ – напряжение Н/м2;
ε – деформация;
А и В – эмпирические константы.
Многочисленные исследования механических свойств костной ткани по разным направлениям показали существование ярко выраженной анизотропии, которая позволяет считать кость ортотропным материалом. То есть биофизически костную ткань можно представить как анизотропную композиционную среду, которая в процессе своего формирования от костной мозоли до компактной кости может быть описана сложной нелинейной реологической моделью, с изменениями в зависимости от степени созревания ее характерных констант.
1.3. Механические свойства сосудистой стенки
Исследования биомеханики сосудистой стенки необходимы, чтобы определить какой вклад сосудистой патологии вносят различные лекарственные вещества при лечении таких заболеваний, как атеросклероз, варикозная болезнь, гипертония и т.д.
Сосуд представляет собой цилиндрическую конструкцию, механическое поведение которой в осевом и круговом отношении является различным. Так, например, удлинение в продольном направлении восходящего отдела аорты больше, чем в поперечном, в среднем на 11%. Существенное влияние на разрушающее напряжение аорты играет возраст человека. В формировании механических свойств ткани важную роль играют отдельные тканевые компоненты сосудистой стенки. Так, удаление коллагена понижает жесткость сосуда на 27%. Удаление мукополисахаридов повышает напряжение ткани при растяжении грудного отдела аорты на 11%. Кроме того, одни лекарственные вещества повышают сосудистый тонус, другие – уменьшают его. Таким образом, механические свойства кровеносных сосудов определяются коллагеном, эластинами, главными мышечными волокнами.
Рассмотрим деформацию сосуда в целом, как результат действия давления p изнутри на упругий цилиндр (рис. 1.4).
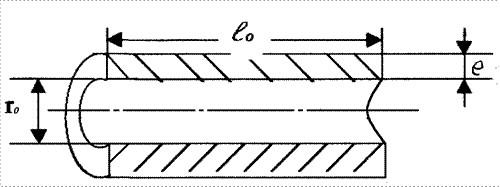
Рис. 1.4. Модель цилиндрического сосуда: r0 - радиус внутренней части сосуда; e - толщина стенки сосуда
Две половины цилиндрического сосуда взаимодействуют между собой по сечениям стенок цилиндра. Площадь (S) этого «сечения взаимодействия» равна 2el0.
Так как σ=F1/S1, то сила взаимодействия двух половинок сосуда будет F1 = 2σel0.
Эта сила уравновешивается силами давления изнутри:
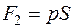 , или
, или 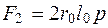 . (1.15)
. (1.15)
Приравнивая силы F1 и F2 и сокращая на 2l0, получим
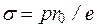 . (1.16)
. (1.16)
Уравнение (1.8) называется уравнением Ламе.
Найдем зависимость  , где E – модуль Юнга.
, где E – модуль Юнга.
 ,
,
отсюда
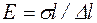 , (1.17)
, (1.17)
где 

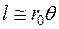 (из рис. 1.5).
(из рис. 1.5).
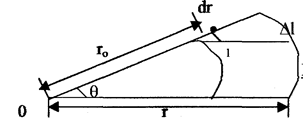
Рис. 1.5. Срез сосуда после относительного удлинения
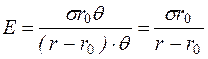 . (1.18)
. (1.18)
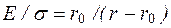 подставим в уравнение (1.8).
подставим в уравнение (1.8).
Получим
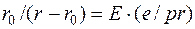 , или
, или 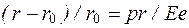 . (1.19)
. (1.19)
Пусть имеем уравнение Ламе
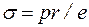 .
.
Будем считать, что при растяжении сосуда объем его стенки не изменяется – площадь сечения стенки возрастает, а толщина убывает, иначе говоря, не изменяется площадь сечения стенки сосуда.
Таким образом, 2πre=const re=b=const, и тогда уравнение Ламе примет вид:
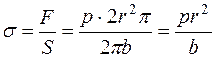 . (1.20)
. (1.20)
Продифференцируем выражение (1.12).
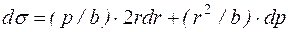 .
.  (1.21)
(1.21)
2. Найдем из закона Гука: 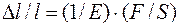 . Обозначим
. Обозначим 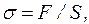
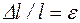 , тогда
, тогда 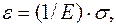
 . Продифференцируем
. Продифференцируем  .
.
Применительно к цилиндрическому сосуду 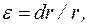 тогда
тогда
 . (1.22)
. (1.22)
Приравнивая формулы (1.13) и (1.14), получим: 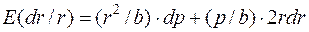 .
.
Найдем dp:
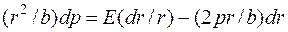 ,
,
Отсюда
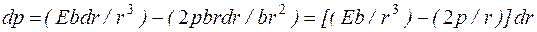 . (1.23)
. (1.23)
Из уравнения (1.15) можно найти связь между давлением, радиусом и модулем Юнга. При решении вопроса о распространении пульсовой волны количественные соотношения получают по данной формуле.
Примерные величины модуля упругости, а также предел прочности при растяжении и сжатии тканей организма представлены в табл. 1.1. Эти данные характерны также для прочности на изгиб. Для сравнения в таб. 1.1 приведены данные, которые касаются некоторых технических материалов.
Из всего вышесказанного можно сделать следующие выводы.
Изучение предела упругости костной, мышечной и сосудистой системы играет значительную роль в жизнедеятельности организма. Так, разрыв сосуда, как правило, ведет к крайней патологии – инсульту, инфаркту миокарда и т.д.
Таблица 1.1
Модули упругости и предел прочности при растяжении для организма и некоторых веществ
| Вид ткани или вещества | Модуль упругости Е, кг·с/м2 | Предел прочности σ, кг·с/м2 |
| Кость | 10-12 | |
| Артерии, вены | 0,4-0,5 | 0,15-0,2 |
| Мышцы | 0,8-1,0 | 0,05-0,1 |
| Связки | 100-150 | 5-7 |
| Сталь | 80-100 | |
| Дерево | 8-10 | |
| каучук | 1,2 |
Знание факторов, влияющих на механические свойства данных систем, позволит решить задачу профилактики грозных заболеваний, а изучение различного рода композиционных материалов, в частности полимеров, дает возможность улучшить вопросы протезирования.
Вопросы для самопроверки
1. Назовите виды деформации. Какая деформация называется упругой?
2. В чем сущность закона Гука?
3. Что называется модулем Юнга? Его физический смысл?
4. Что называется твердостью? Хрупкостью?
5. Какие вещества называются кристаллическими? аморфными?
6. Сделайте вывод уравнения Ламе. В чем сущность механики сосудистой стенки?
7. Уравнение Хилла. Что оно выражает?
8. К каким веществам относят жидкие кристаллы?
9. Что называется анизотропией?
10. На какие виды по молекулярной упорядоченности делятся жидкие кристаллы?
11. Какие вещества относят к полимерам?
12. Какие виды механических нагрузок действуют на опорно-двигательный аппарат?
13. В какой зависимости находится скорость сокращения мышц согласно закону Хилла?
14. В чем сущность теории Фанга упругого поведения биологических тканей?
15. Напишите математическое выражение закона Фанга.
16. что собой представляет костная ткань с точки зрения композиционного материала?
17. Что влияет на формирование упругости и эластичности сосудистой стенки?
18. Как, с биофизической точки зрения, можно представить костную ткань?
19. Каков механизм мышечного сокращения?
20. В чем сущность уравнения Ламе?
21. Найдите зависимость между давлением, радиусом сосуда и модулем Юнга.
22. Объясните процесс сокращения мышц.
23. В чем сущность теории А. Хасли механики сокращения мышечной системы?
Типовые тесты текущего контроля
1. Сделайте выбор уравнений Ламе и Гука?
1) ε=kσ;
2) σ=alnε+b;
3) 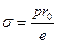
2. Выберите уравнение Хилла.
1)  ;
;
2) 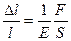 ;
;
3) 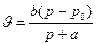
3. Выберите уравнение характеризующее жидкое состояние вещества
1) Emin<<kT [Дж];
2) Emin  kT [Дж];
kT [Дж];
3) Emin>>kT [Дж].
Задачи для закрепления изучаемого материала
1. Длина большеберцовой кости у лежащего человека равна 40 см, площадь поперечного сечения ее в среднем равна 700 мм2. Определить уменьшение6 длины кости к человека, когда он стоит, если его масса 70 кг. Модуль Юнга 4,5·1010 Па.
2. Объемная плотность растянутой мышцы 1,2 кДж/м3, при относительном удлинении 5%. Какова величина упругого напряжения в мышце? Какова величина модуля упругости мышцы при этих условиях?
3. Сухожилие длинной 75 мм и площадью поперечного сечения 80 мм2 при нагрузке 9,5 Н удлиняется на 15 мм. Определить модуль упругости для этого сухожилия и вычислить для него объемную плотность энергии.
4. Определить толщину стенки локтевой кости, если ее разрыв произошел при осевой нагрузке 1295 Н. Внешний диаметр кости в месте разрыва 13 мм, предел прочности на разрыв 16,2 МПа.
5. Вычислить величину упругого напряжения, возникающего при подвешивании к портняжной мышце лягушки грузика массой 10 г. Площадь сечения мышцы 2,7 мм2. Какова робота, необходимая для растяжения мышцы под действием веса грузика, если ее длина возросла от 25 мм до 34 мм? Модуль упругости мышцы при этом растяжении равен 0,95 Мпа.
6. Определить силу необходимую для удлинения сухожилия S=4мм2 на 0,02 его первоначальной длины. Модуль Юнга считать равным 10 Н/м2.
7. Модуль Юнга протоплазменных нитей, измеренный у некоторых клеток с помощью микроигл, оказывается равным 9·103 Н/м2 при комнатной температуре. Определить напряжение, действующее на нить, при растяжениях, не превышающих 20 см ее первоначальной длины.
8. Какая работа совершается при растяжении на 1 мм мышцы длиной 5см и диаметром 4мм? Модуль Юнга упругости кости принять равным 9,8- 106H/м2.
9. Какая сила необходима для разрушения при сжатии бедренной кости диаметром 30мм и толщиной стенок 3мм, если предел прочности кости 1,4·108 Н/м2?
лекция 2. Термодинамика биологических сред
Термодинамикой называется наука, которая занимается изучением условий и количественных соотношений превращения энергии из одних видов в другие. Термодинамические законы впервые были выведены французским ученым С. Карно. Изучение тепловых процессов, происходящих в механических системах, в дальнейшем было продолжено в трудах Р. Клаузиуса, Л. Больцмана и других ученых XIX и XX столетий. В последнее время термодинамика все больше проникает в биологию, так как данный метод позволяет произвести энергетический анализ почти всех физиологических процессов, протекающих как на молекулярном уровне, так и в целом организме.
2.1. Основные термодинамические понятия и величины. Первое начало термодинамики
В физике системой называется совокупность рассматриваемых тел. Причем системой может служить жидкость и находящийся в равновесии с ней пар. Система может состоять и из одного тела. В термодинамике различают три вида систем.
1. Изолированная система. Процессы, происходящие в изолированной системе, не реагируют со средой, так как не происходит обмена с окружающей средой ни веществом, ни энергией. Безусловно, такая система идеальна и в природе не существует.
2. Закрытая система. Это система, в которой происходящие процессы могут взаимодействовать с окружающей средой в виде обмена энергиями, но не веществами. Примером закрытой системы является герметически закрытый сосуд, в котором, например, протекает экзотермическая биохимическая реакция. В данном случае система отдает окружающей среде тепло, но веществом с ней не обменивается.
3. Открытая система. Это система, которая обменивается с окружающей средой как энергией, так и веществом. Все живые организмы - открытые системы, так как необходимым условием жизнедеятельности является постоянный обмен веществом и теплом со средой.
В период развития термодинамики все термодинамические законы были выведены для изолированных и закрытых систем. В настоящее время в биофизике разрабатываются и используются термодинамические законы для открытых систем.
Дата добавления: 2020-11-18; просмотров: 454;











