Дифференциал функции.
Пусть функция у=ƒ(х) имеет в точке х отличную от нуля производную 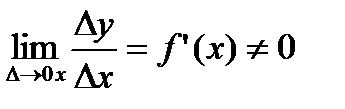 . Тогда, по теореме о связи функции, ее предела и бесконечно малой функции, можно записать
. Тогда, по теореме о связи функции, ее предела и бесконечно малой функции, можно записать
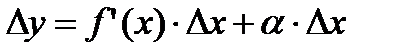 , (2.12)
, (2.12)
где α→0 при ∆х→0.
Таким образом, приращение функции ∆у представляет собой сумму двух слагаемых: 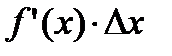 и
и 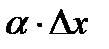 , являющихся бесконечно малыми при ∆x→0. При этом первое слагаемое есть бесконечно малая функция одного порядка с ∆х, так как
, являющихся бесконечно малыми при ∆x→0. При этом первое слагаемое есть бесконечно малая функция одного порядка с ∆х, так как 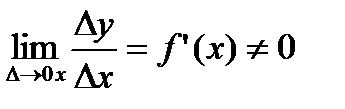 а второе слагаемое есть бесконечно малая функция более высокого порядка, чем ∆х:
а второе слагаемое есть бесконечно малая функция более высокого порядка, чем ∆х:
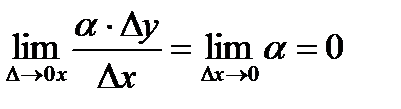 . (2.13)
. (2.13)
Поэтому первое слагаемое 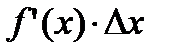 называют главной частью приращения функции ∆y. Дифференциалом функции
называют главной частью приращения функции ∆y. Дифференциалом функции 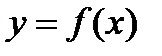 в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается
в точке х называется главная часть ее приращения, равная произведению производной функции на приращение аргумента, и обозначается 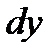 (или
(или 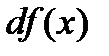 ):
):
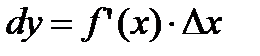 (2.14)
(2.14)
Дифференциал 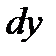 называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной х, т. е. дифференциал функции
называют также дифференциалом первого порядка. Найдем дифференциал независимой переменной х, т. е. дифференциал функции 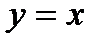 .
.
Так как 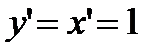 , то, согласно формуле (2.1), имеем
, то, согласно формуле (2.1), имеем 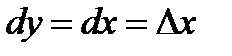 , т. е. дифференциал независимой переменной равен приращению этой переменной:
, т. е. дифференциал независимой переменной равен приращению этой переменной:
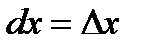 . (2.15)
. (2.15)
Поэтому формулу (2.14) можно записать так:
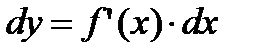 , (2.16)
, (2.16)
иными словами, дифференциал функции равен произведению производной этой функции на дифференциал независимой переменной.
Из формулы (2.16) следует равенство
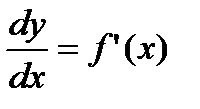 . (2.17)
. (2.17)
Теперь обозначение производной 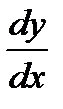 можно рассматривать как отношение дифференциалов
можно рассматривать как отношение дифференциалов 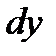 и
и 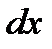 .
.
Пример 2.13
Найти дифференциал функции 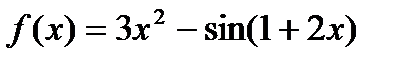 .
.
Решение:
По формуле 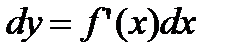 находим
находим 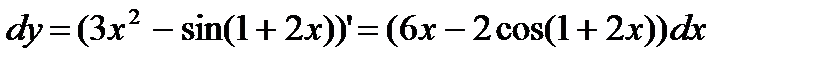
Пример 2.14. Найти дифференциал функции 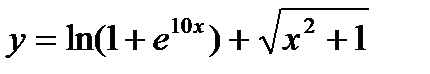 . Вычислить
. Вычислить 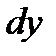 при
при 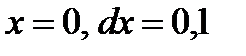 .
.
Решение: 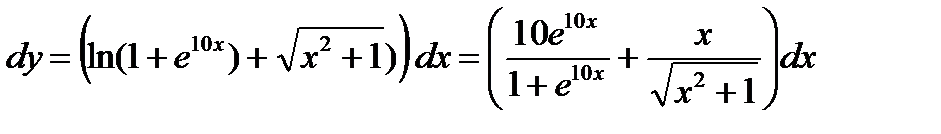 .
.
Подставив 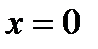 и
и 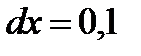 , получим
, получим 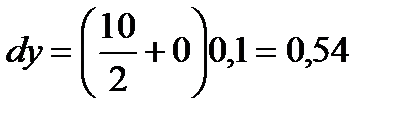 .
.
Дата добавления: 2020-11-18; просмотров: 544;











