Возрастание и убывание функции, ее экстремумы
Рассмотрим функцию 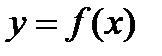 , непрерывную вместе со своей производной на некотором промежутке. Геометрический смысл производной заключается в том, что
, непрерывную вместе со своей производной на некотором промежутке. Геометрический смысл производной заключается в том, что 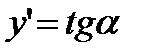 , где
, где 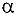 -угол наклона касательной к положительному направлению оси Oх.
-угол наклона касательной к положительному направлению оси Oх.
|
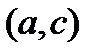 ). Касательные, проведенные к кривой
). Касательные, проведенные к кривой 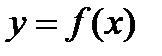 в любой точке этого промежутка, образуют с осью
в любой точке этого промежутка, образуют с осью 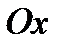 тупой угол, тангенс которого отрицателен, т. е. для
тупой угол, тангенс которого отрицателен, т. е. для 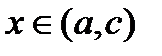 величина
величина 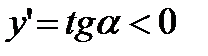 . Значит, если функция убывает на некотором промежутке, то ее производная на этом промежутке отрицательна.
. Значит, если функция убывает на некотором промежутке, то ее производная на этом промежутке отрицательна.
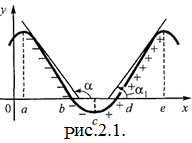
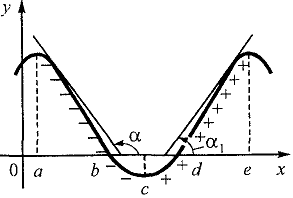
Если с возрастанием значения аргумента х значение функции yвозрастает, то функция является возрастающей (на рис. в интервале 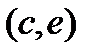 ).Касательные, проведенные к кривой у = f(х) в любой точке этого промежутка, образуют с осью Ох острый угол, тангенс которого положителен, т. е. для
).Касательные, проведенные к кривой у = f(х) в любой точке этого промежутка, образуют с осью Ох острый угол, тангенс которого положителен, т. е. для 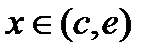 величина
величина 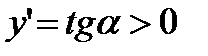 . Значит, если функция возрастает на некотором промежутке, то ее производная на этом промежутке положительна.
. Значит, если функция возрастает на некотором промежутке, то ее производная на этом промежутке положительна.
Теорема. Если функция f(x) имеет положительную производную в каждой точке интервала l, то эта функция возрастает на этом интервале. Если функция f(x) имеет отрицательную производную в каждой точке интервала l, то эта функция убывает на этом интервале.
Замечание. Интервалы, в которых функция возрастает или убывает, называются интервалами монотонного изменения функции.
Мы предположили, что наша функция и ее производная непрерывны, а значит они меняют знаки с «-» на «+» или с «+» на «-» только при переходе через нуль, т. е. в тех точках, в которых интервал убывания сменяется интервалом возрастания, (в которых у' = 0). В этих точках мгновенная скорость изменения функции равна нулю. Точки области определения функции, в которых производная функции равна нулю, бесконечности или не существует, называются критическими. На рис. 2.1. имеются три критические точки а, с, е.
Пример.2.7.Найти интервалы монотонного изменения функции
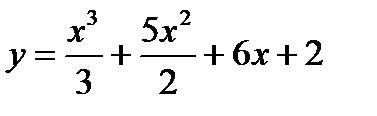
Решение.Найдем производную: 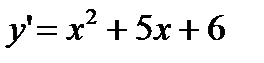 .
.
Эта функция непрерывна. Чтобы найти критические точки, приравняем производную нулю и найдем корни полученного уравнения:
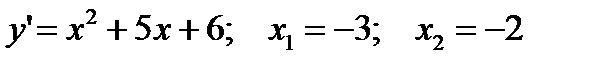
Разобьем числовую прямую на интервалы: 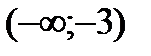 ;
; 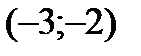 ;
; 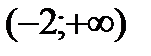 .
.
Определим знак производной в каждом из интервалов. В результате определим участки возрастания-убывания функции.
| x | 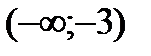
| 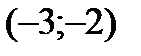
| 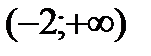
|
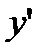
| + | - | + |
| y | возрастает | убывает | возрастает |
Таким образом, при 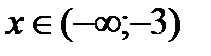 и
и 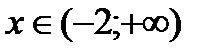 функция возрастает, при
функция возрастает, при 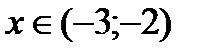 - убывает.
- убывает.
Наименьшее значение функции в окрестности некоторой точки 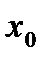 называют минимальным значением (min), а наибольшее ее значение - максимальным (max). Дадим строгое определение этим понятиям.
называют минимальным значением (min), а наибольшее ее значение - максимальным (max). Дадим строгое определение этим понятиям.
Точка 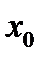 из области определения функции f называется точкой минимума этой функции, если у этой точки есть окрестность
из области определения функции f называется точкой минимума этой функции, если у этой точки есть окрестность 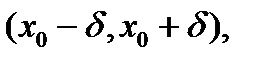 во всех точках которой, не совпадающих с точкой
во всех точках которой, не совпадающих с точкой 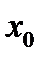 ,
,
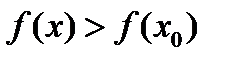 (2.7)
(2.7)
Точка 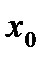 из области определения функции f называется точкой максимумаэтой функции, если у этой точки есть окрестность
из области определения функции f называется точкой максимумаэтой функции, если у этой точки есть окрестность 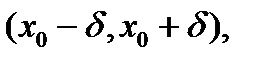 во всех точках которой, не совпадающих с точкой
во всех точках которой, не совпадающих с точкой 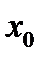 ,
,
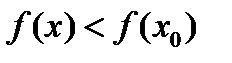 (2.8)
(2.8)
Максимумы и минимумы называются экстремумами функции.
Замечание.Так как речь идет об экстремальных значениях функции в окрестностях некоторых точек, то иногда определенные нами экстремумы называются локальными экстремумами.
У непрерывной функции точки минимума и максимума обязательно чередуются.
Рассмотрим необходимое условие существования экстремума.
Теорема Ферма. Если внутренняя точка xо из области определения непрерывной функции f(х) является точкой экстремума и в этой точке существует производная, то она равна нулю, т. е.
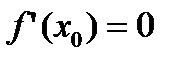 (2.9)
(2.9)
Пример. 2.8. Исследовать на экстремум функцию 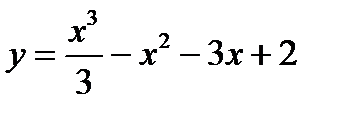 .
.
Решение. Функция 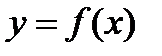 точек разрыва не имеет. Область определения – вся числовая ось. Исследуем данную функцию на экстремум. Определим критические точки. Для этого находим первую производную данной функции и приравниваем ее к нулю:
точек разрыва не имеет. Область определения – вся числовая ось. Исследуем данную функцию на экстремум. Определим критические точки. Для этого находим первую производную данной функции и приравниваем ее к нулю: 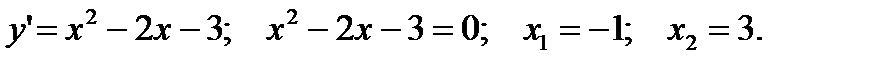
Разобьем числовую прямую на интервалы: 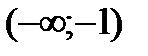 ;
; 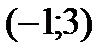 ;
; 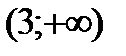 .
.
Определим знак производной в каждом из интервалов. В результате определим участки возрастания-убывания функции.
| x | 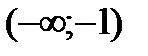
| 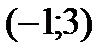
| 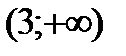
| |||
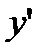
| + | - | + | |||
| y | max при 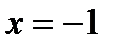
| min при 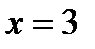
| ||||
При 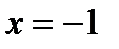 производная меняет знак с «плюса» на «минус», то есть в этой точке функция имеет максимум. Для определения значения этого минимума подставим в первоначальное выражение функции
производная меняет знак с «плюса» на «минус», то есть в этой точке функция имеет максимум. Для определения значения этого минимума подставим в первоначальное выражение функции 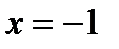 , в результате получим
, в результате получим 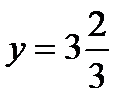 .
.
При 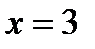 производная меняет знак с «минуса» на «плюс», то есть в этой точке функция имеет минимум. Для определения значения этого максимума подставим в первоначальное выражение функции
производная меняет знак с «минуса» на «плюс», то есть в этой точке функция имеет минимум. Для определения значения этого максимума подставим в первоначальное выражение функции 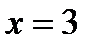 , в результате получим
, в результате получим 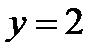 .
.
Таким образом, функция 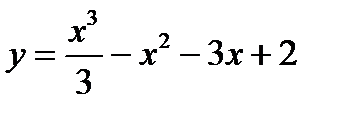 имеет две точки экстремума:
имеет две точки экстремума:
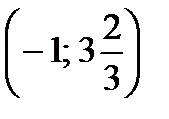 - максимум;
- максимум; 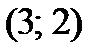 - минимум.
- минимум.
Дата добавления: 2020-11-18; просмотров: 630;











