Методы интегрирования
I. Непосредственное интегрирование.
Этот способ интегрирования предполагает такое преобразование подынтегральной функции, которое позволило бы использовать для решения табличные интегралы.
Пример 3.3. Найти 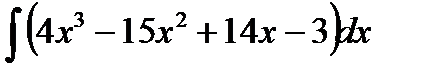
Решение.Воспользуемся свойством 2. интеграла: интеграл от суммы (разности) функций равен сумме (разности) интегралов от этих же функций.
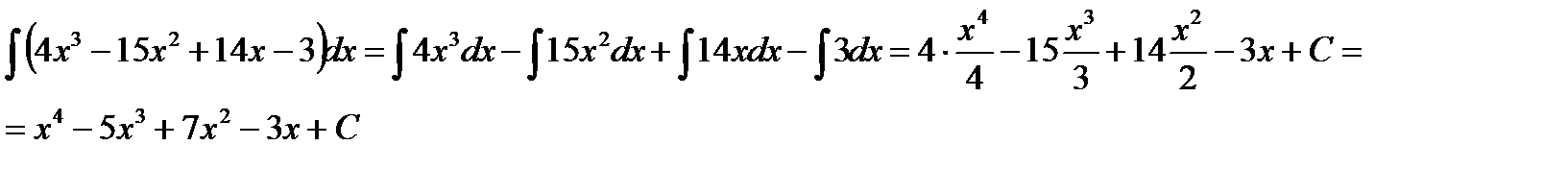
Пример 3.4.Найти 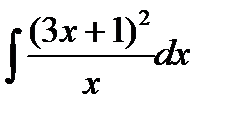
Решение.Приведем интеграл к табличному виду. Для этого раскроем скобки в числителе и разделим почленно числитель на знаменатель.
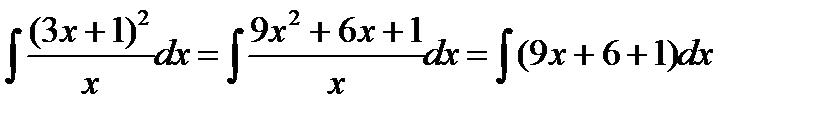
Затем воспользуемся указанным выше свойством интеграла суммы (разности) функций: 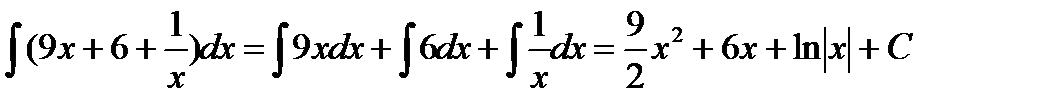
II.Метод подстановки.
Этот метод называют также методом замены переменной. Использование этого метода основано на свойстве 3 интеграла.
Пример 3.5. Найти 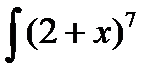
Решение.Введем новую переменную: 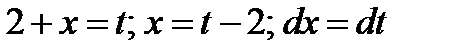 .
.
Найдем интеграл: 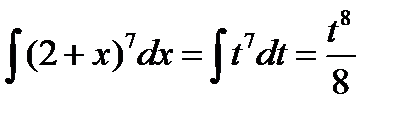
Выразим результат через первоначальный аргумент: 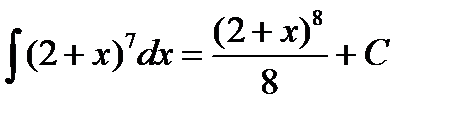
Пример 3.6.Найти 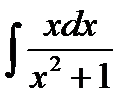
Решение. Сделаем подстановку 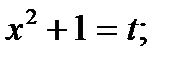 Надо определить, чему равен dx. Для этого продифференцируем выражение
Надо определить, чему равен dx. Для этого продифференцируем выражение 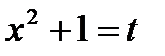 , в результате чего получим
, в результате чего получим 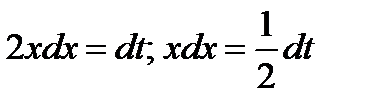 .
.
Подставим все это в первоначальный интеграл, в результате чего будем иметь:
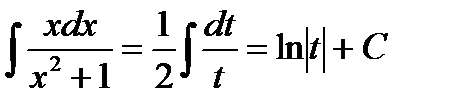
Выразим результат через первоначальный аргумент: 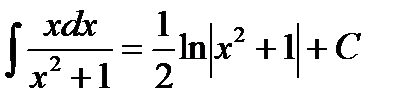
Этот пример дает возможность сделать следующий общий вывод: 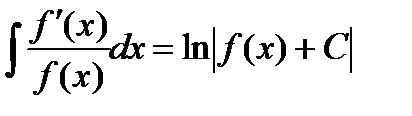 .
.
III. Метод интегрирования по частям.
Использование этого метода основано на свойстве (4) интеграла: 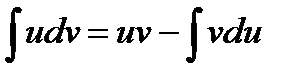
Пример 3.7. Найти 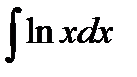 .
.
Решение. Обозначим 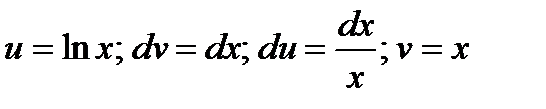 .
.
Подставим полученные данные в первоначальное выражение:
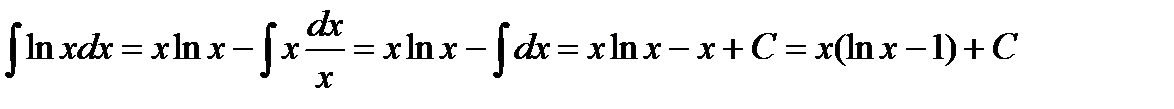
Пример 3.8. Найти 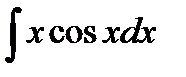 .
.
Решение.Интегрируем по частям
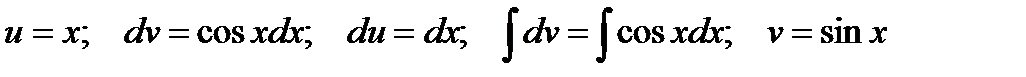
Тогда 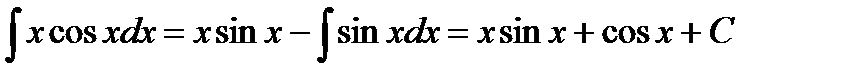
Пример 3.9. Найти 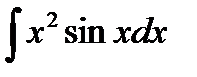
Решение.Интегрируем по частям
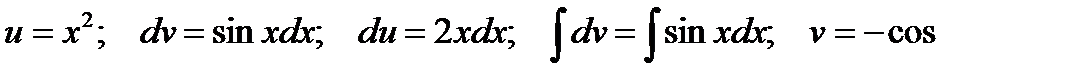
Тогда 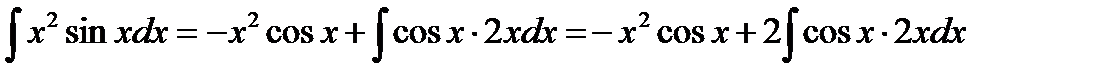 .
.
Подставим значение интеграла из примера 3.8, получим
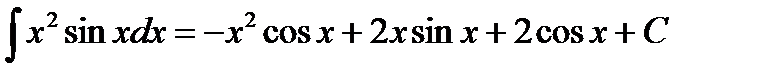
Дата добавления: 2020-11-18; просмотров: 544;











