Производные элементарных функций
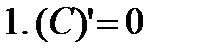
| 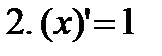
| 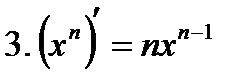
| 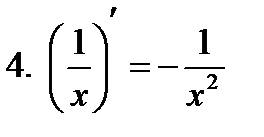
| 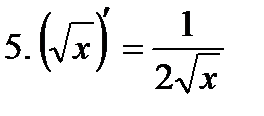
|
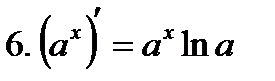
| 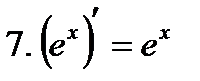
| 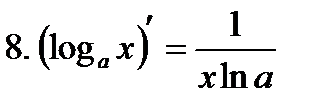
| 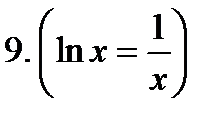
| 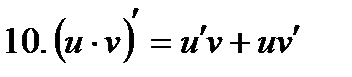
|
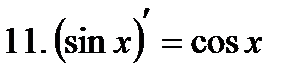
| 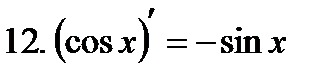
| 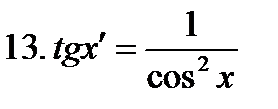
| 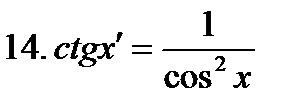
| 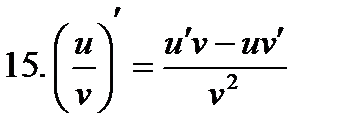
|
Теорема 1(производная суммы функций). Если в точке х функции 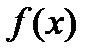 и
и 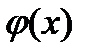 имеют производные, то производная от суммы (разности) этих функций в точке х существует и равна сумме (разности) производных этих функций:
имеют производные, то производная от суммы (разности) этих функций в точке х существует и равна сумме (разности) производных этих функций:
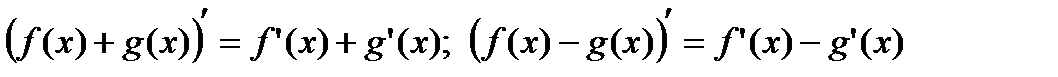 (2.2)
(2.2)
Пример 2.1.Найти у', если 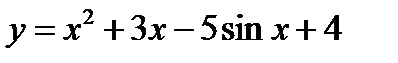 .
.
Решение. 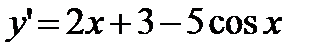
Теорема 2 (производная произведения функций). Если в точке х функции 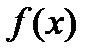 и
и 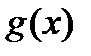 имеют производные, то в точке х произведение этих функций имеет производную, которая равна сумме произведений одной из данных функций и производной другой
имеют производные, то в точке х произведение этих функций имеет производную, которая равна сумме произведений одной из данных функций и производной другой
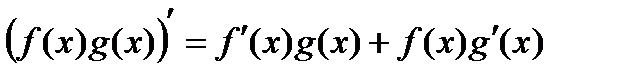 (2.3)
(2.3)
Пример 2.2. Найти у', если 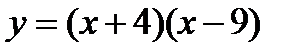 .
.
Решение.Обозначив 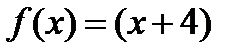 и
и 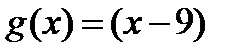 будем иметь
будем иметь 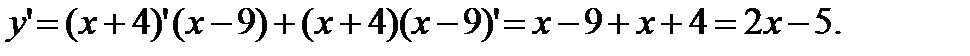
Следствие. Постоянный множитель можно выносить за знак производной: 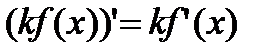 (2.4)
(2.4)
Теорема 3(производная частного двух функций). Если в точке х функции 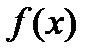 и
и 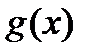 имеют производные, причем в точке х функция
имеют производные, причем в точке х функция 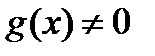 , то частное этих функций имеет в точке х производную, которая вычисляется по формуле
, то частное этих функций имеет в точке х производную, которая вычисляется по формуле
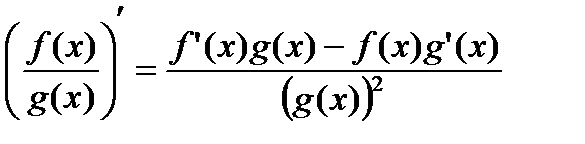 (2.5)
(2.5)
Пример 2.3.Найти у', если 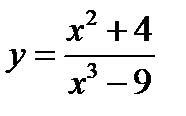 .
.
Решение.Обозначив 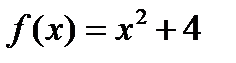 и
и 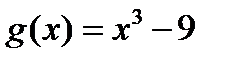 будем иметь
будем иметь
Теорема 5 (производная сложной функции). Если в точке х функция 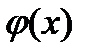 имеет производную
имеет производную 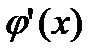 , а в точке
, а в точке 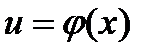 функция
функция 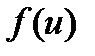 имеет производную
имеет производную 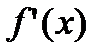 , то производная от сложной функции
, то производная от сложной функции 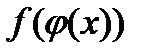 в точке х существует и определяется по формуле:
в точке х существует и определяется по формуле:
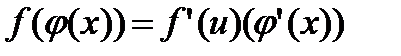 , (2.6)
, (2.6)
где 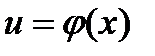 .
.
Пример 2.4.Найти 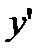 , если
, если 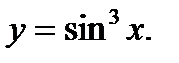
Решение.Функция 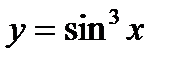 - сложная. Во-первых, она – степенная, во вторых – тригонометрическая. Поэтому
- сложная. Во-первых, она – степенная, во вторых – тригонометрическая. Поэтому 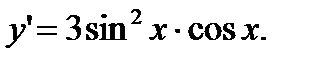
Пример 2.5.Найти 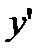 , если
, если 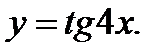
Решение. 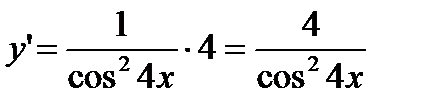
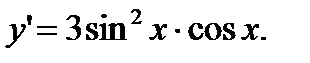
Пример 2.6.Найти 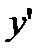 , если
, если 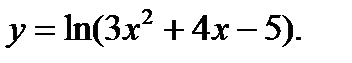
Решение. 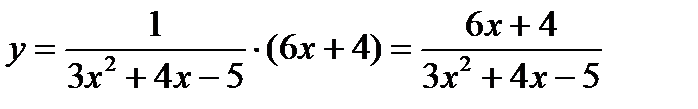
Дата добавления: 2020-11-18; просмотров: 547;











