Геометрическая интерпретация комплексных чисел
Определение и алгебраическая форма комплексных чисел
Комплексными числаминазываются выражения вида 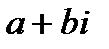 , (где а и b действительные числа, а
, (где а и b действительные числа, а 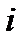 - символ, удовлетворяющий условию
- символ, удовлетворяющий условию 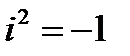 ), при условии, что для этих выражений равенство, сложение и умножение определяются следующим образом:
), при условии, что для этих выражений равенство, сложение и умножение определяются следующим образом:
а) два комплексных числа 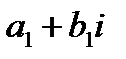 и
и 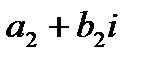 считаются равными тогда и только тогда, когда
считаются равными тогда и только тогда, когда 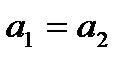 и
и 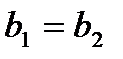
б) суммой двух комплексных чисел 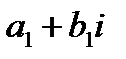 и
и 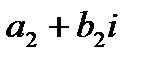 называется комплексное число
называется комплексное число 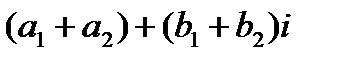 (1.1),
(1.1),
в) произведением двух комплексных чисел 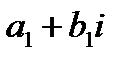 и
и 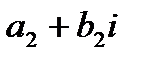 называется комплексное число
называется комплексное число 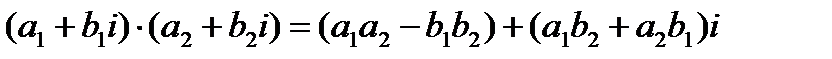 (1.2).
(1.2).
Пример. 1.1. Вычислить сумму и произведение двух комплексных чисел: 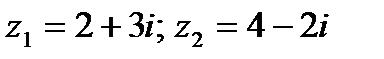
Решение.
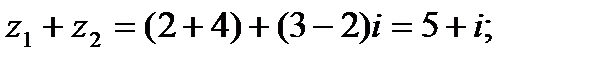
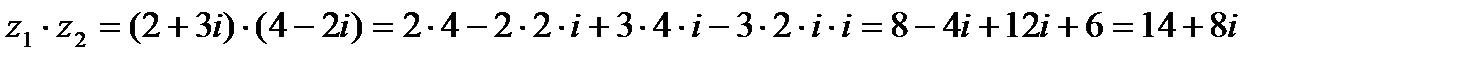
Из приведенных примеров видно, что формулы (1.1) и (1.2.) помнить необязательно. Сложение и умножение комплексных чисел можно выполнять по правилам сложения и умножения двучленов.
Разность двух комплексных чисел – операция обратная сложению и может быть выполнена по формуле: 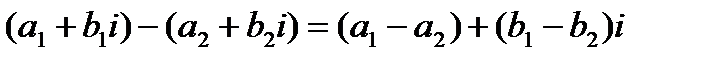 (1.3).
(1.3).
Пример 1.2. Вычислить разность двух комплексных чисел: 
Решение
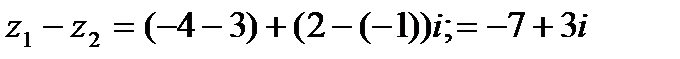
Из приведенного примера видно, что формулу (1.3) помнить необязательно. Вычитание комплексных чисел можно выполнять по правилам вычитания двучленов
Число 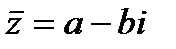 называется комплексно-сопряженным с комплексным числом
называется комплексно-сопряженным с комплексным числом 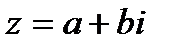 . Понятие комплексной сопряженности взаимно.
. Понятие комплексной сопряженности взаимно.
Сумма и произведение комплексно-сопряженных чисел соответственно равны 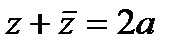 и
и 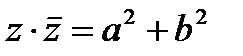 .
.
Частноеот деления одного комплексного числа на второе – операция обратная умножению и может быть выполнена по формуле:
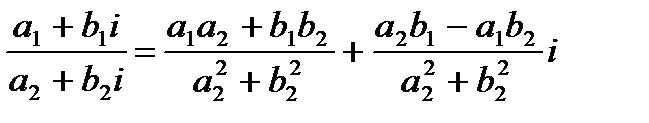 (1.4)
(1.4)
Эту формулу можно не запоминать, а руководствоваться следующим правилом: для того, чтобы разделить одно комплексное число на другое, надо записать их в виде дроби, в числителе которой – делимое, а в знаменателе – делитель, а затем числитель и знаменатель умножить на число, сопряженное со знаменателем.
Покажем справедливость этого правила:
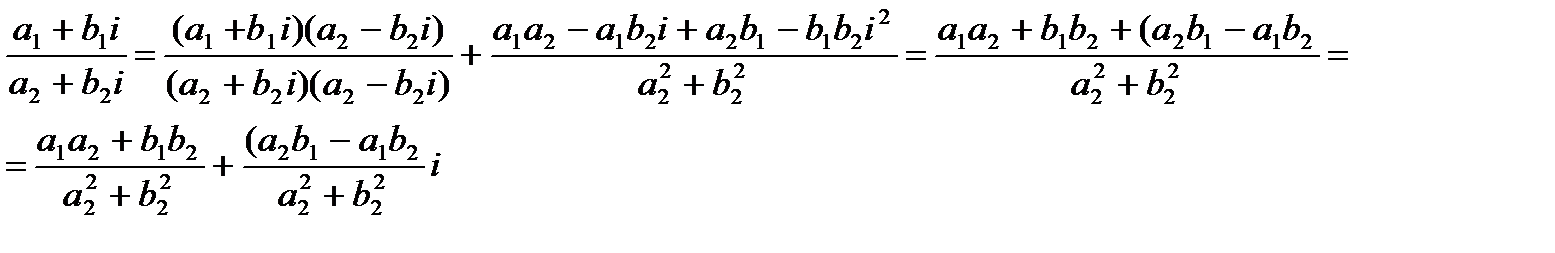
Как можно увидеть, получившееся в результате использования приведенного выше правила деления комплексных чисел совпадает с правой частью формулы (1.4), что свидетельствует о справедливости этого правила.
Пример 1.3.
Вычислить частное от деления комплексного числа 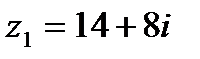 на комплексное число
на комплексное число 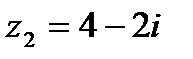
Решение

В этом примере использованы по сути те же данные, что и во втором из примеров 1.1. В данном случае делимое – результат перемножения комплексных чисел примера 1.1. Делитель – второй из сомножителей упомянутого примера. Частное от деления в текущем примере совпало с первым сомножителем примера 1.1., что подтверждает правильность выполненной нами операции деления.
Комплексное число равно нулю тогда и только тогда, когда 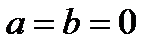 .
.
Для комплексных чисел, так же, как и для векторов, нет понятия больше и меньше.
Покажем, как в множестве комплексных чисел решаются квадратные уравнения, дискриминанты которых меньше нуля.
Пусть, например, нужно решить уравнение 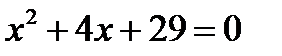 . Легко подсчитать, что
. Легко подсчитать, что
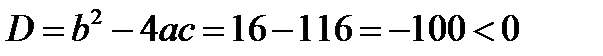
Следовательно,
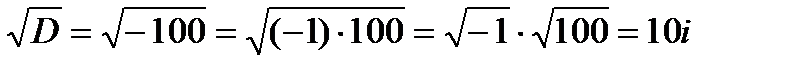 .
.
Поэтому
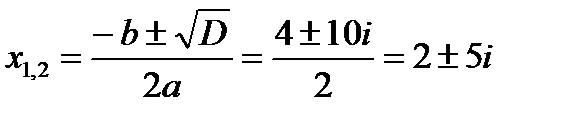
То есть, квадратное уравнение с действительными коэффициентами и отрицательным дискриминантом имеет два комплексно-сопряженных корня.
Операция возведения в степень комплексного числа рассматривается как частный случай произведения одного и того же сомножителя.
Степени мнимой единицы даются формулой
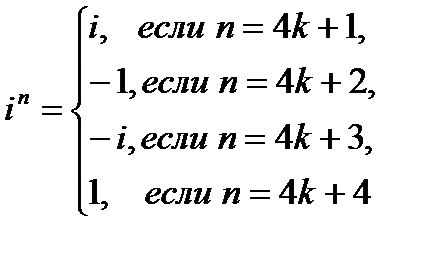
Например, 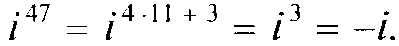
Пример 1.4. Найти действительные числа х и yиз уравнения 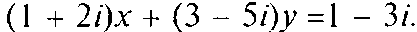
Решение.Используем условия равенства двух комплексных чисел 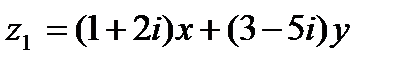 и
и 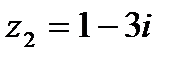 .
.
Пользуясь определением суммы, получаем 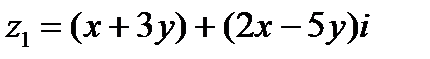 Сравнивая действительные и мнимые части чисел z1 и z2, получим систему двух уравнений относительно х и у
Сравнивая действительные и мнимые части чисел z1 и z2, получим систему двух уравнений относительно х и у 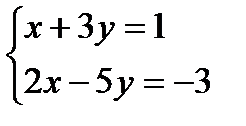 , решением которой будет
, решением которой будет 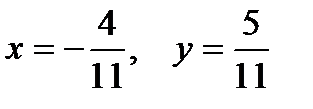 .
.
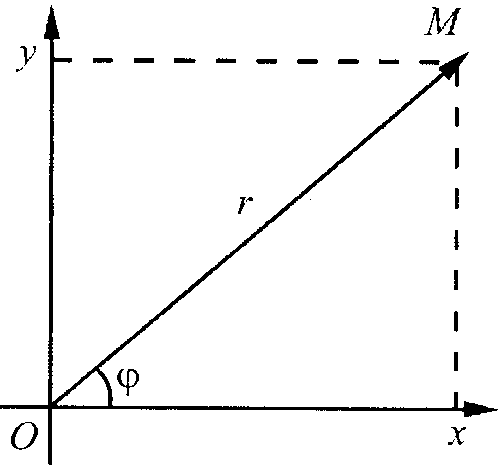
Геометрическая интерпретация комплексных чисел
|
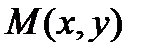 . Но эта же точка, если она отлична от начала координат, может быть задана и полярными координатами
. Но эта же точка, если она отлична от начала координат, может быть задана и полярными координатами 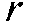 и
и 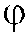 . Декартовы координаты могут быть вычислены через полярные координаты следующим образом:
. Декартовы координаты могут быть вычислены через полярные координаты следующим образом:
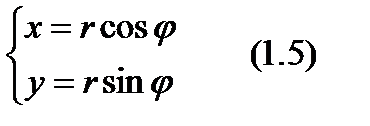
По Декартовым координатам можно вычислить полярные координаты точки:
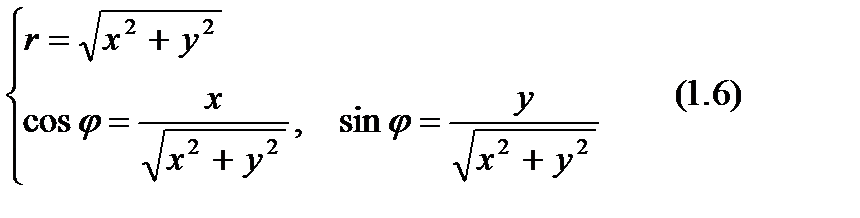
Точке М(0; 0) соответствует r = 0; 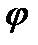 не определен.
не определен.
Пример 1.5. В полярной системе координат постройте точки:  .
.
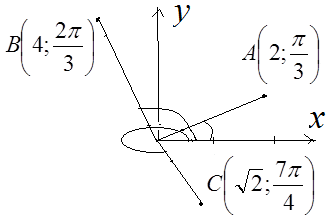 Решение.
Решение.
Пример 1.6. Найдите полярные координаты точек, симметричных с точками
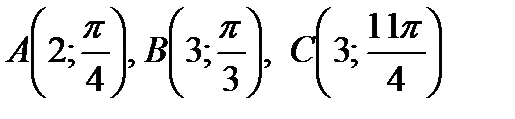
а) относительно полюса б) относительно полярной оси.
Решение.
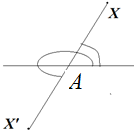
а) Центральной симметрией относительно точки A называют преобразование пространства, переводящее точку X в такую точку X′, что A — середина отрезка XX′ (см. рис.).
 Поэтому, в каждой из приведенных точек величина радиус-вектора r останется прежней, а угол
Поэтому, в каждой из приведенных точек величина радиус-вектора r останется прежней, а угол 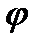 изменится на величину
изменится на величину 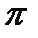 . Таким образом, координаты точек, симметричных с указанными точками относительно начала координат, будут:
. Таким образом, координаты точек, симметричных с указанными точками относительно начала координат, будут: 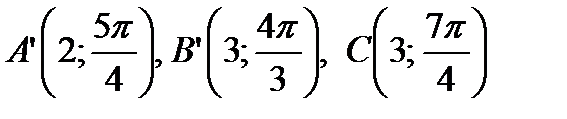
б) Для того, чтобы построить на плоскости точку 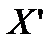 , симметричную точке
, симметричную точке 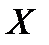 относительно прямой l, необходимо от этой точки провести перпендикуляр к прямой и отложить на продолжении этого перпендикуляра точку
относительно прямой l, необходимо от этой точки провести перпендикуляр к прямой и отложить на продолжении этого перпендикуляра точку 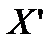 на расстоянии, равном расстоянию от точки
на расстоянии, равном расстоянию от точки 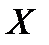 до прямой (см. рис.).
до прямой (см. рис.).
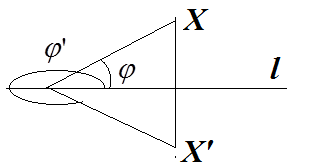 Из приеденного рисунка видно, что в точке
Из приеденного рисунка видно, что в точке 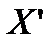 , симметричной точке
, симметричной точке 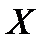 , радиус-вектор равен радиус - вектору точки
, радиус-вектор равен радиус - вектору точки 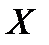 , а угол
, а угол 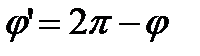 .
.
Таким образом, координаты точек, симметричных с указанными точками относительно оси  , будут:
, будут: 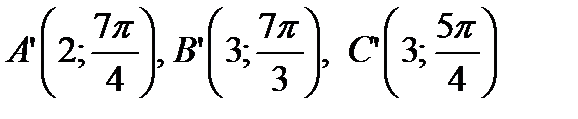
Пример 1.7. Определите полярные координаты точек 
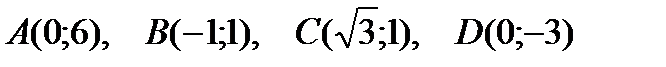
Решение:
Точка A: 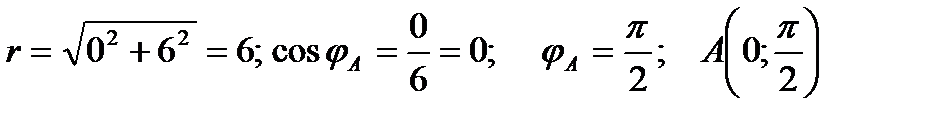 ;
;
Точка B: 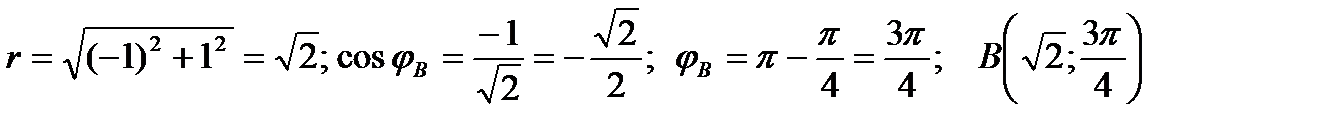 ;
;
Точка C: 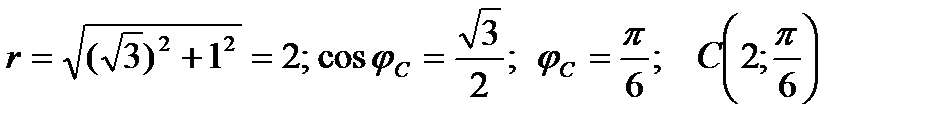 ;
;
Точка D: 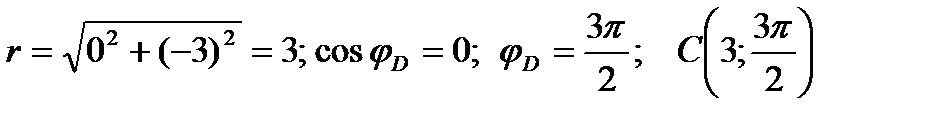
Аналогично тому, как на числовой прямой откладываются точки с декартовыми координатами, на плоскости можно откладывать точки, соответствующие комплексным числам.
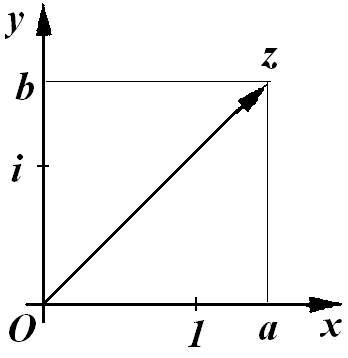 Пусть дано множество комплексных чисел C и
Пусть дано множество комплексных чисел C и 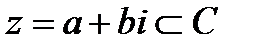 - произвольное комплексное число.
- произвольное комплексное число.
За единицу на оси Ox примем действительное число 1, а на оси Оу - мнимую единицу 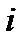 . Такая плоскость называется комплексной плоскостью.
. Такая плоскость называется комплексной плоскостью.
Пример 1.7. Данные числа изобразите на комплексной плоскости
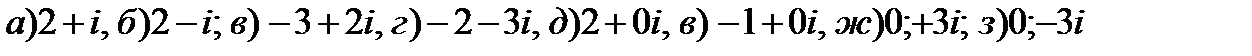 Решение
Решение
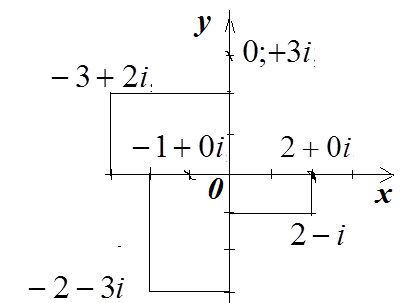
Дата добавления: 2020-11-18; просмотров: 644;











