Тригонометрическая форма комплексных чисел
Если на плоскости выбрать прямоугольную систему координат Оху, то каждое комплексное число можно изобразить точкой с координатами а и b. Всякое комплексное число z может быть представлено в тригонометрической форме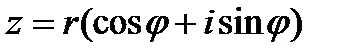 
.
Число r является модулем, а угол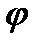 
- аргументом комплексного числа z.
Если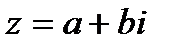 
, то 
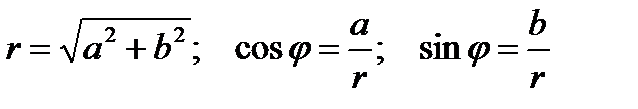. (1.7).
Модуль комплексного числа z обозначается еще |z|, а аргумент – arg z. Для модулей двух произвольных комплексных чисел справедливы неравенства
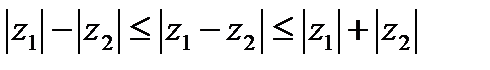
Комплексные числа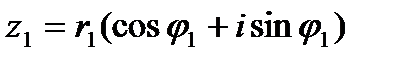 
и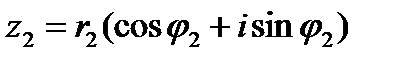 
(заданные в тригонометрической форме) умножаются и делятся соответственно по формулам
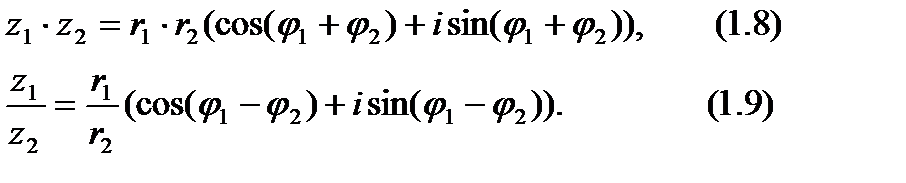
Возведение комплексного числа в целую положительную степень осуществляется по формуле:
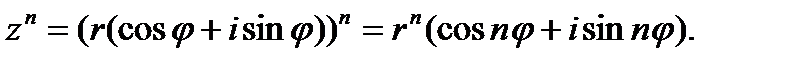(1.10).
Равенство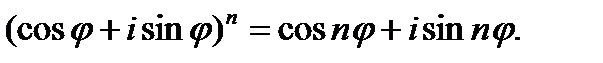 
называется формулой Муавра.
Извлечение корня n-й степени из комплексного числа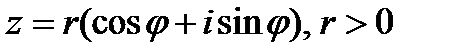 
, дает n различных значений, которые можно найти по формуле
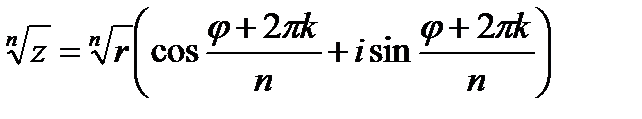, (1.11)
где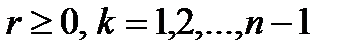 
.
В частности,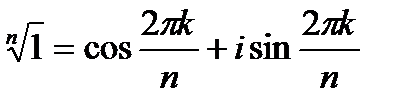 
, 
.
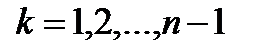На комплексной плоскости эти точки находятся в вершинах правильного многоугольника, с центром в точке (0; 0), одна из вершин этого многоугольника находится в точке (1; 0).
Пример 1.8. Записать комплексное число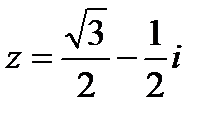 
в тригонометрической форме.
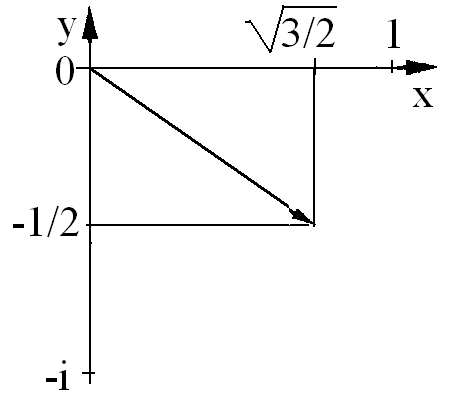Решение.Построим данное число на комплексной плоскости (см. рис.).
Модуль (радиус-вектор) комплексного числа:
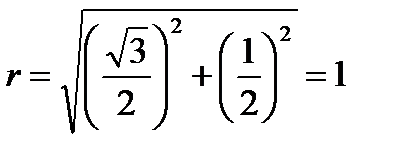
Его аргумент (угол наклона радиус-вектора к оси x)равен:
.
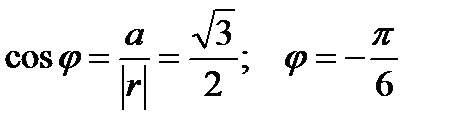Знак «минус» обусловлен тем, что конец радиус-вектора находится в четвертой четверти комплексной плоскости.
В тригонометрической форме комплексное число записывается в виде:
.
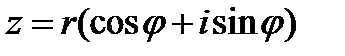Следовательно, заданное число запишется в виде
.
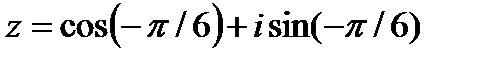Пример 1.9. Даны два комплексных числа в тригонометрической форме: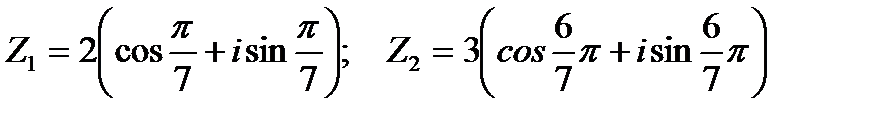 
. Записать их произведение и частное от деления первого числа на второе.
Решение.
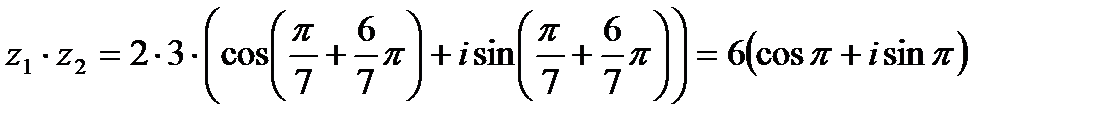
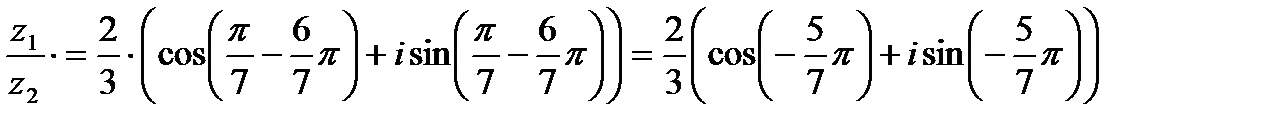
Пример 1.10. Дано комплексное число в алгебраической форме: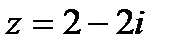 
а) перевестиего в тригонометрическую форму;
б) возвести в четвертую степень;
в) извлечь корень третьей степени.
Решение.
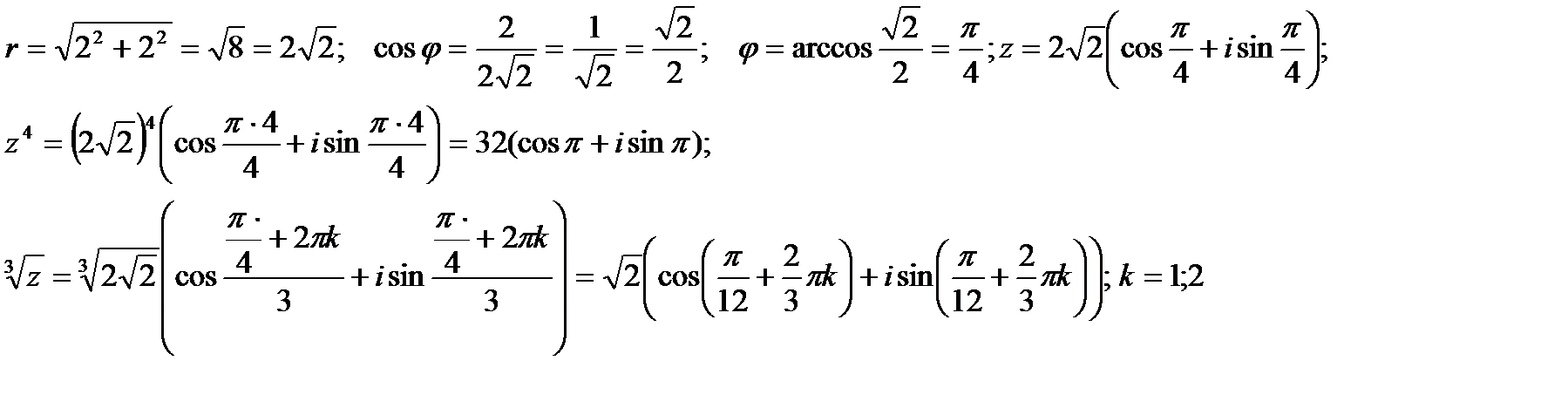
Дата добавления: 2020-11-18; просмотров: 354;
Поиск по сайту
Узнать еще
- CASE-технология создания информационных систем
- E) Расчет структурных составляющих очага деформации с одним нейтральным сечением
- I. Информационные жанры.
- II. Формализация процесса формирования математических моделей
- III. Неопределенная форма глагола (инфинитив).
- III. Репрезентативный интеллект и формальные операции
- IV. Матричная форма организации
- IV. Раскрытие информации в бухгалтерской отчетности
Публикации по технике и механике
Публикации по биологии
Публикации по информатике
Публикации по строительству
Публикации по физике
Публикации по химии
Публикации по электронике
Публикации по искусству
Публикации по истории
