Тема: Определение корреляционной связи между высотой растений и влажностью почвы

Цель работы: получение практических навыков определения наличия корреляционной связи между разными признаками у сопряженных вариациионных рядов.

Задание: Определить наличие корреляционной связи между двумя сопряженными признаками, путем вычисления коэффициента корреляции. В результате проведенных исследований получены высоты однолетних саженцев тополя (гибрид «Казахстанский»), выращенных в различных условиях водообеспеченности (влажность почвы, выражена в процентах от ПВ). В результате исследований получены:

высоты растений (см): 200, 205, 203, 203, 194, 190, 190, 175, 177, 178, 179, 201, 205, 160, 165, 165, 197, 198, 198, 200, 200;

влажность почвы (%): 75, 77, 77, 75, 72, 72, 72, 60, 70, 71, 71, 75, 75, 69, 69,69, 73, 73, 74, 75, 75. Варианты высот обозначаем у, а влажность почвы – х. Составляем таблицу из пяти вертикальных столбцов. В первые два столбца заносим варианты рядов (табл. 1).

Таблица 1

Высота растений (см) и влажность почвы (% от ПВ)

Силу связи между высотой растений и влажностью почвы определяем по формуле вычисления коэффициента корреляции для невзвешенных рядов:

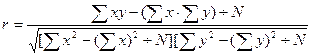, где r- коэффициент корреляции; х- варианты ряда аргумента; у- варианты ряда функции; N- объем выборки, то есть число пар вариант, или объем одного из рядов х или у.

Вычисления производим в следующем порядке:

1. Возводим в квадрат значения х и у (столбцы 3 и 4); 2. Перемножаем по строкам значения х на у (столбец 5); 3 Суммируем величины столбцов 1-5, получаем: ∑х = …; ∑у =…; ∑ х² = …; ∑у² = 7…; ∑ху = …; 4 Возводим в квадрат суммы столбцов 1 и 2: (∑х)²=…; (∑у)²= …; 5. Перемножаем итог столбца х на итог столбца у: ∑х ∑у = .

2. Подставляем, полученные значения, в формулу и определяем коэффициент корреляции.

Вычисленный коэффициент корреляции показывает на довольно тесную (слабую) связь между изучаемыми признаками.

Ответить на вопросы:

1. Для чего рекомендуется составление корреляционной решетки?

2. Коэффициент корреляции можно определить лишь по приведенной в данной работе формуле или существуют другие способы его вычисления?

3. Отличается ли техника определения коэффициента корреляции для малых и больших вариационных рядов?

Литература:

1. Зайцев Г.Н. Математическая статистика в экспериментальной ботанике / Г.Н.Зайцев. – М.: Наука, 1984. – с. 130-175.
2. Федоров А.И. Методы математической статистики в биологии и опытном деле / А.И.Федоров. – Алма-Ата: Казгосиздат, 1957. – с. 84-129.