У дуба черешчатого (Quercus robur L.)

Порядок работы и схема вычислений.

М_х=…; М_у= …; N_x= …: N_y= ….

Средние квадратические отклонения вычисляются по формулам:

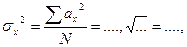
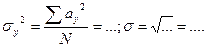
Коэффициент корреляции определяем в конкретном примере по формуле, предложенной в свое время Бравэ:

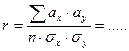
Принимая во внимание, что коэффициент корреляции изменяется в пределах от 0 до +1 при прямой и от 0 до -1 при обратной связи, следует сделать заключение, что значение равное … свидетельствует о довольно тесной связи (об отсутствии связи) между изменчивостью длины и диаметра желудей. Степень установленной (не установленной) прямой связи выражается …% от полной непрерывной связи, при которой значение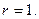

Определяем степень надежности или достоверности найденной величины коэффициента корреляционной связи. Для решения этого вопроса необходимо вычислить ошибку коэффициента корреляции по формуле:

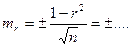
Следовательно, коэффициент корреляции равен … ± …. Степень надежности определяется по формуле: 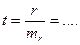Вычисленный показатель превышает (не превышает) табличное значение критерия Стьюдента. Следовательно, коэффициент корреляции вполне надежен (не надежен).

Ответить на вопросы:

1. Раскройте суть понятия корреляции.

2. Как определяется коэффициент корреляции для малых выборок?

3. По какой формуле определяется ошибка коэффициента корреляции?

Литература:

1. Зайцев Г.Н. Математическая статистика в экспериментальной ботанике / Г.Н.Зайцев. – М.: Наука, 1984. – с. 130-175.
2. Федоров А.И. Методы математической статистики в биологии и опытном деле / А.И.Федоров. – Алма-Ата: Казгосиздат, 1957. – с. 84-129.