В виде ранжированного вариационного ряда

N = …. ∑ х = …. ∑а = …. ∑ (х –А)² = а² = ….

3. Вычисляем среднюю арифметическую по формуле:

М _ср. = ∑ х / N = …

4. Ближайшее к М целое число А = … (условное среднее) используем для получения условных отклонений по формуле а = х – А = … и результаты вносим в столбец второй табл. 1. Суммируем отклонения с учетом их знаков (∑а = ….). Производим проверку вычислений по формуле: ∑а = ∑х – NА. Равенство обеих частей уравнения соблюдается (не соблюдается), следовательно, вычисления верны (неверны).

5. Возводим в квадрат условные отклонения (столбец третий, табл.1) и суммируем эти квадраты: (∑а² =…).

6. Определяем дисперсию по формуле: = …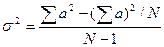

7. Определяем прочие параметры статистического ряда:

Ошибка средней арифметической: …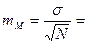

Критерий достоверности средней арифметической: …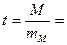

Ошибка сигмы: ….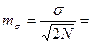

Коэффициент вариации: …..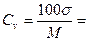

Ошибка коэффициента вариации: ….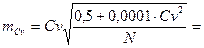

Показатель точности опыта: ….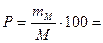

Ошибка показателя точности опыта: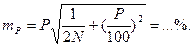

Определение медианы:

находим номер медианной варианты, который равен 0,5 (N+1) =….

При четном числе вариант, за медиану принимается середина промежутка между двумя центральными вариантами, при нечетном числе вариант - принимается центральная варианта. В нашем случае Ме = … см.

В результате получены параметры, дающие довольно полное представление о статистическом не взвешенном ряде.

Проанализировать полученные показатели можно следующим образом: средняя арифметическая высоты растений вариационного ряда, составляет …см, с доверительным интервалом на 0,95 уровне равным (по таблице значение критерия Стьюдента для нашего вариационного ряда, при числе степеней свободы v = N -1 = …, ( табл. значение t = 2,145) , вычисленное t =…., значительно превышает (не превышает) табличное значение, что показывает на высокий (низкий) критерий достоверности. Показатель точности опыта (P = …) значительно ниже (выше) пяти процентов, что определяет достаточную точность исследований.

Средняя арифметическая - М = … см; ошибка средней арифметической - m =… см.

Варьирование высот растений сравнительно невелико (велико), так как коэффициент вариации Cv = …. Полученные параметры заслуживают (не заслуживают) доверия в виду большой (не большой) достоверности средней арифметической t_M = …> 3 ( меньше 3) и значения показателя точности опыта, меньшего (большего) 5% (Р = …) .

Ответить на вопросы:

1. Объясните для чего используется условная средняя?

2. Приведите формулы для определения дисперсии и среднего квадратического отклонения.

3. Дайте определение медианы, моды и показателя эксцесса.

4. Приведите формулу вычисления ошибки средней арифметической.

Литература:

1. Зайцев Г.Н. Математическая статистика в экспериментальной ботанике / Г.Н.Зайцев. – М.: Наука, 1984. – с. 39-59.

2. Любимов В.Б. Методические рекомендации по применению математической статистики в экспериментальной экологии и биологии / В.Б.Любимов, Е.Б.Смирнова, К.В.Балина. – Балашов: СГУ, 1999. – с.6-8.

3. Федоров А.И. Методы математической статистики в биологии и опытном деле / А.И.Федоров. – Алма-Ата: Казгосиздат, 1957. – с. 23-49.