Высоты саженцев от влажности почвы

M_y и М_х – средние арифметические рядов - у и х. М_х =…; М_у=…;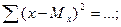

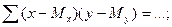
Коэффициенты а₀ и а₁ определяются в данном примере по формулам:

.

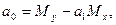
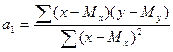Ошибка уравнения и точки пересечения прямой с осями координат вычисляются формулам: 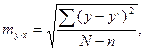у = а₀, х = - (а₀/а₁).

Если известны средние квадратические отклонения рядов х и у и коэффициент корреляции между ними, то величины коэффициентов а₁ и а₀ уравнения прямой линии, не вычисляя точек эмпирической линии регрессии, можно определить по формулам: 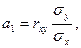или 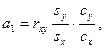где а₁ – коэффициент регрессии при аргументе х; r_xy- коэффициент корреляции между признаками х и у; 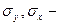сигмы рядов у и х в исходных единицах; s_y, s_x – сигмы тех же рядов в классовых интервалах; с_у и с_х – классовые интервалы рядов у и х. В данном случае свободный член а₀ вычисляется по формуле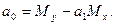

Ответить на вопросы:

1.Для какой цели служит коэффициент регрессии?

2.Для каких целей составляются корреляционные таблицы?

Литература:

1. Зайцев Г.Н. Математическая статистика в экспериментальной ботанике / Г.Н.Зайцев. – М.: Наука, 1984. – с. 175-250.
2. Федоров А.И. Методы математической статистики в биологии и опытном деле / А.И. Федоров. – Алма-Ата: Казгосиздат, 1957. – с. 103-129.