К вычислению моментов ряда распределений

Прежде чем переходить к вычислению условных моментов, проверим выполненные действия. Сумма чисел столбца 11 должна быть равна следующему выражению: .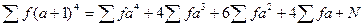

Вычисляем условные моменты распределения (моментами распределения называют средние степени отклонений вариант от средней арифметической - это центральные моменты, а средние степени отклонений от произвольного числа называются условными моментами). Порядок момента равен степени, в которую возводится отклонение. Условные моменты вычисляются для получения возможности вычисления центральных моментов.

…; …; …; …;

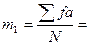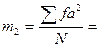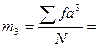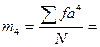По следующим формулам:

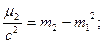
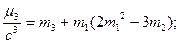
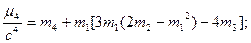
где 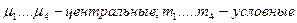момент, вычисляем правую часть уравнений:

Находим центральные моменты из уравнений:

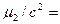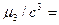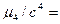…; …; …, где с - классовый интервал, тогда:

…; …; …

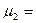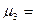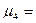Вычисляем: среднюю арифметическую (M= A+ m₁c.):

среднее квадратическое отклонение ;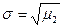

коэффициент асимметрии:

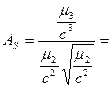…; эксцесс: … .

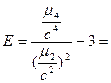Коэффициент вариации: … .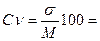

Дать анализ результатам исследований.

Ответить на вопросы:

1. Для чего используются условные моменты распределения?

2. Раскройте суть понятия коэффициента асимметрии.

3. Дайте характеристику условным и центральным моментам.

Литература:

1. Зайцев Г.Н. Математическая статистика в экспериментальной ботанике / Г.Н.Зайцев. – М.: Наука, 1984. – с. 42-130.

2. Любимов В.Б. Методические рекомендации по применению математической статистики в экспериментальной экологии и биологии / В.Б.Любимов, Е.Б.Смирнова, К.В.Балина. – Балашов: СГУ, 1999. – с. 9-14.

3. Федоров А.И. Методы математической статистики в биологии и опытном деле / А.И.Федоров. – Алма-Ата: Казгосиздат, 1957. – с. 23-49.