Анализ результатов функционального синтеза системы электропривода
Функциональный синтез системы электропривода (СЭП) численными методами фактически осуществляется путем реализации инверсных уравнений. Инверсные уравнения для звеньев структурной схемы СЭП составляют на основе «прямых» уравнений для этих же звеньев. Примеры разработки инверсных уравнений для разомкнутых СЭП и систем электропривода с обратной связью с использованием численного метода А. В. Башарина (без итераций) приведены в литературе.
В параграфе 19.3 была рассмотрена задача функционального синтеза разомкнутой системы электропривода (СЭП) при управлении пуском (рис. 17).

Рис. 17. Блок-схема разомкнутой СЭП
При решении задачи была использована структурная схема модели СЭП (рис. 18) и на ее основе получены по методу А. В. Башарина (без итераций) инверсные уравнения (54) - (57) для определения момента двигателя 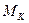 , тока якоря
, тока якоря 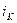 , напряжения силового преобразователя
, напряжения силового преобразователя 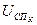 и
и 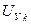 на «
на «  » шаге при реализации функционального синтеза.
» шаге при реализации функционального синтеза.
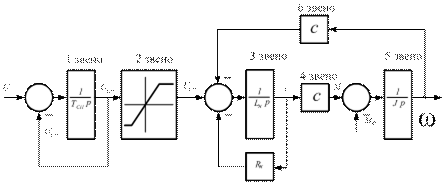
Рис. 18. Детализированная структурная схема разомкнутой СЭП
 . (54)
. (54)
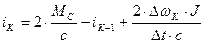 . (55)
. (55)
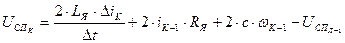 . (56)
. (56)
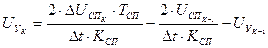 . (57)
. (57)
Наряду с методом А. В. Башарина (без итераций) для составления инверсных уравнений может быть применен классический параллельный метод Эйлера.
При выводе инверсных уравнений классическим методом были использованы уравнения состояния, подготовленные для звеньев детализированной структурной схемы разомкнутой СЭП (рис. 18).
 . (58)
. (58)
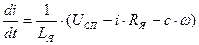 . (59)
. (59)
Нелинейная зависимость  .
.
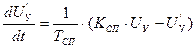 , (60)
, (60)
где 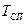 -постоянная времени силового преобразователя;
-постоянная времени силового преобразователя;
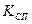 -коэффициент передачи силового преобразователя на первом линейном участке его характеристики;
-коэффициент передачи силового преобразователя на первом линейном участке его характеристики;
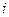 -ток якоря ДПТ с независимым возбуждением;
-ток якоря ДПТ с независимым возбуждением;
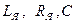 -индуктивность, сопротивление якоря и постоянная ДПТ;
-индуктивность, сопротивление якоря и постоянная ДПТ;
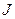 -момент инерции механической части СЭП;
-момент инерции механической части СЭП;
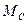 -момент нагрузки ДПТ. В работе принято, что
-момент нагрузки ДПТ. В работе принято, что 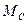 =const.
=const.
Инверсное уравнение для 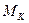 в классическом методе составлено на основе уравнения (5) с использованием численного метода Эйлера.
в классическом методе составлено на основе уравнения (5) с использованием численного метода Эйлера.
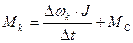 . (61)
. (61)
Приращение скорости определяется по формуле 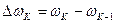 .
.
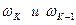 - значения скорости ЭП на «
- значения скорости ЭП на «  » и «
» и « 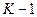 » шаге синтеза, определяемые при табличном задании зависимости скорости
» шаге синтеза, определяемые при табличном задании зависимости скорости 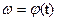 с применением интерполяции.
с применением интерполяции.
Выражение для тока 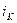 определяется при делении
определяется при делении 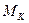 на значение постоянной двигателя
на значение постоянной двигателя 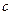 .
.
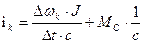 , (62)
, (62)
где 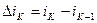 .
.
Инверсное уравнение для 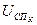 в классическом методе получено на основе уравнения (63).
в классическом методе получено на основе уравнения (63).
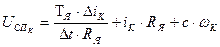 , (63)
, (63)
Силовой преобразователь (СП) обладает нелинейной характеристикой  , которая может быть задана в табличной форме. Значения
, которая может быть задана в табличной форме. Значения 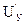 определяются по зависимости
определяются по зависимости  с применением интерполяции. Силовой преобразователь также характеризуется динамическими свойствами, которые представлены апериодическим звеном, соединенным последовательно с нелинейным звеном с характеристикой
с применением интерполяции. Силовой преобразователь также характеризуется динамическими свойствами, которые представлены апериодическим звеном, соединенным последовательно с нелинейным звеном с характеристикой  .
.
Инверсное уравнение для 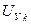 выведено при использовании формулы (64).
выведено при использовании формулы (64).
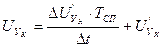 . (64)
. (64)
Приращение 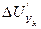 определяется по формуле
определяется по формуле 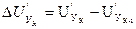 .
.
Для сравнения результатов синтеза по классическому методу и по методу А. В. Башарина (без итераций) была составлена программа синтеза на языке, принятом в программном пакете Matlab с использованием М - файлов, по алгоритму, представленному в описании к Matlab. При исследовании методов синтеза приняты несколько вариантов заданных зависимостей скорости от времени  . Среди них: линейная, экспоненциальная, синусоидальная и параболическая зависимости.
. Среди них: линейная, экспоненциальная, синусоидальная и параболическая зависимости.
На рис. 19 приведен один из вариантов графика желаемой зависимости скорости от времени  при изменении
при изменении 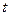 в пределах от 0 до 0.6 с. График
в пределах от 0 до 0.6 с. График  таблично формируется с помощью двух массивов для скоростей
таблично формируется с помощью двух массивов для скоростей 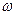 , состыкованных при
, состыкованных при 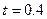 с. Первый массив определяет экспоненциальный характер зависимости скорости от времени
с. Первый массив определяет экспоненциальный характер зависимости скорости от времени  для
для 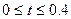 с (
с ( 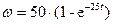 ), а второй формирует линейную зависимость
), а второй формирует линейную зависимость 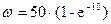 рад/с в интервале от 0.4 до 0.6 с (
рад/с в интервале от 0.4 до 0.6 с ( 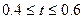 ).
).
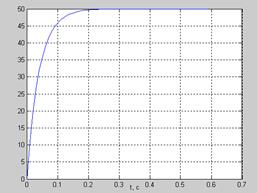
Рис. 19. Зависимость скорости от времени 
Формирование зависимости скорости от времени  в виде двух участков реализуется следующим фрагментом программы, представленным в виде М – файла.
в виде двух участков реализуется следующим фрагментом программы, представленным в виде М – файла.
t1=0:0.0001:0.4;
w=50*(1-exp(-25*t1));
t1=[t1 0.41:0.19:0.6];
w=[w 50*(1-exp([-25*0.4 -25*0.4]))];
Постоянная времени ТС экспоненциального участка заданной зависимости скорости  равна 0.04 с. Таким образом, практический переход к участку постоянной скорости осуществляется за время, равное (3
равна 0.04 с. Таким образом, практический переход к участку постоянной скорости осуществляется за время, равное (3 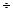 5)ТС и составляет примерно 0.2 с.
5)ТС и составляет примерно 0.2 с.
Для корректного представления графиков при расчетах с применением М-файлов (Matlab) необходимо, чтобы шаг синтеза 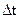 был больше или равен шагу
был больше или равен шагу 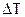 между узлами функций, заданных графически (или таблично), т.е.
между узлами функций, заданных графически (или таблично), т.е. 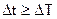 . Это связано с тем, что при синтезе, в отличие от моделирования, применяемого при анализе СЭП, используется операция дифференцирования функций и согласуется с рекомендациями, приведенными в литературе.
. Это связано с тем, что при синтезе, в отличие от моделирования, применяемого при анализе СЭП, используется операция дифференцирования функций и согласуется с рекомендациями, приведенными в литературе.
При исследовании системы СЭП были приняты следующие параметры.
Шаг синтеза 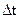 =0.001 с.
=0.001 с.
Постоянная времени ТЯ цепи якоря при исследовании варьировалась в пределах от 0.01 до 0.15 с.
Коэффициент передачи двигателя 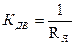 равен 15.
равен 15.
Коэффициент передачи 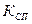 силового преобразователя на линейном нарастающем участке его нелинейной характеристики принят равным 20.
силового преобразователя на линейном нарастающем участке его нелинейной характеристики принят равным 20.
Постоянная времени 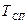 силового преобразователя при расчетах изменялась в пределах от 0.01 до 0.05 с.
силового преобразователя при расчетах изменялась в пределах от 0.01 до 0.05 с.
Нелинейная характеристика (рис. 20) реализуется следующим фрагментом программы, представленным в виде М – файла.
uy1=[-20000 -10 0 10 20000];
usp1=[-200.1 -200 0 200 200.1];
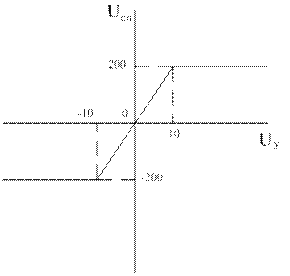
Рис. 20. Нелинейная характеристика управления силового преобразователя 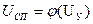
Момент нагрузки принят активным и равным 100 Нм.
Момент инерции системы электропривода при исследовании варьировался в пределах от 1 до 10.
Постоянная двигателя равна 2 Вс/рад.
Конечное время синтеза ограничено значением 0.6 с, что связано с максимальным временем при задании зависимости скорости  .
.
При исследовании синтеза СЭП по численному методу А. В. Башарина (без итераций) были получены результаты, которые могут быть оценены как «расходящиеся» (рис. 21).
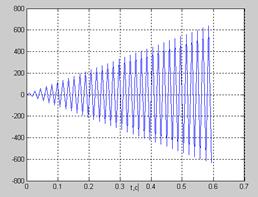
Рис. 21. Зависимость напряжения управления силового преобразователя от времени 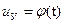 при использовании численного метода А. В. Башарина
при использовании численного метода А. В. Башарина
При исследовании синтеза по классическому численному методу результаты для звеньев СЭП и в целом для системы электропривода по характеру и по точности соответствуют результатам, полученным в аналитической форме.
Задачи синтеза системы электропривода (СЭП) отличаются от задач анализа неоднозначными решениями. Во-вторых, трудности решения задач синтеза значительно выше, так как при их реализации используются операции дифференцирования функций. Для исследования этих проблем был рассмотрен функциональный синтез разомкнутой СЭП с записью временных зависимостей входных сигналов для каждого звена системы.
С целью анализа результатов синтеза было составлено несколько программ синтеза в пакете Matlab с использованием М – файлов. В каждой программе в качестве заданной (желаемой) зависимости скорости от времени  использовался один из возможных вариантов. Среди них: линейная, экспоненциальная, синусоидальная и параболическая зависимости. Алгоритмы при разработке программ базируются на следующих инверсных уравнениях звеньев, использующих численный метод Эйлера.
использовался один из возможных вариантов. Среди них: линейная, экспоненциальная, синусоидальная и параболическая зависимости. Алгоритмы при разработке программ базируются на следующих инверсных уравнениях звеньев, использующих численный метод Эйлера.
Инверсное уравнение для механической части СЭП.
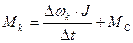 , (65)
, (65)
где 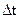 - шаг синтеза;
- шаг синтеза;
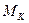 - значение момента двигателя на «К» шаге синтеза;
- значение момента двигателя на «К» шаге синтеза;
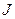 -момент инерции механической части СЭП;
-момент инерции механической части СЭП;
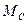 -момент нагрузки СЭП. В работе принято, что
-момент нагрузки СЭП. В работе принято, что 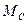 =const.
=const.
Приращение скорости определяется по формуле 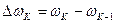 .
.
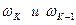 - значения скорости ЭП на «
- значения скорости ЭП на «  » и «
» и « 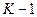 » шаге синтеза, определяемые при табличном задании зависимости скорости
» шаге синтеза, определяемые при табличном задании зависимости скорости 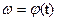 с применением интерполяции.
с применением интерполяции.
Инверсное уравнение для цепи якоря двигателя постоянного тока (ДПТ).
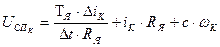 , (66)
, (66)
где 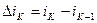 ;
;
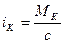 - значение тока двигателя на «
- значение тока двигателя на «  » шаге синтеза;
» шаге синтеза;
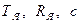 - постоянная времени цепи якоря, сопротивление якоря и постоянная ДПТ;
- постоянная времени цепи якоря, сопротивление якоря и постоянная ДПТ;
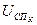 - напряжение на выходе силового преобразователя на «
- напряжение на выходе силового преобразователя на «  » шаге синтеза.
» шаге синтеза.
Инверсное уравнение для звена, учитывающего динамические свойства силового преобразователя.
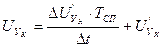 , (67)
, (67)
где 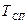 - постоянная времени силового преобразователя;
- постоянная времени силового преобразователя;
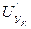 - напряжение управления на входе звена, учитывающего нелинейные свойства силового преобразователя;
- напряжение управления на входе звена, учитывающего нелинейные свойства силового преобразователя;
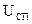 - напряжение управления на входе СЭП;
- напряжение управления на входе СЭП;
Приращение 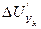 определяется по формуле
определяется по формуле 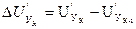 .
.
На рис. 22 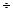 25 приведены зависимости скорости от времени
25 приведены зависимости скорости от времени  для линейного, экспоненциального, синусоидального и параболического законов соответственно.
для линейного, экспоненциального, синусоидального и параболического законов соответственно.
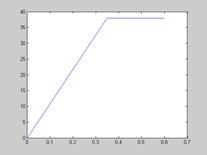
Рис. 22. Линейная зависимость скорости от времени 
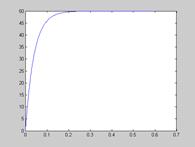
Рис. 23. Экспоненциальная зависимость скорости от времени 

Рис. 24. Синусоидальная зависимость скорости от времени 
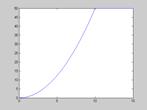
Рис. 25. Параболическая зависимость скорости от времени 
На рис. 26 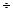 29 представлены зависимости
29 представлены зависимости 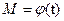 для указанных выше заданных зависимостей скоростей СЭП. Синтез был проведен при следующих значениях параметров:
для указанных выше заданных зависимостей скоростей СЭП. Синтез был проведен при следующих значениях параметров: 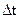 =0.001 с;
=0.001 с; 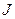 =2
=2 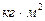 ;
; 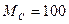
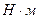 .
.

Рис. 26. Зависимость момента от времени 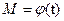 для линейной зависимости скорости СЭП
для линейной зависимости скорости СЭП
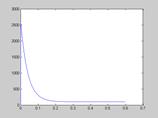
Рис. 27. Зависимость момента от времени 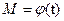 для экспоненциальной зависимости скорости СЭП
для экспоненциальной зависимости скорости СЭП
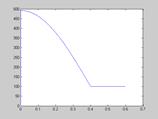
Рис. 28. Зависимость момента от времени 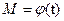 для синусоидальной зависимости скорости СЭП
для синусоидальной зависимости скорости СЭП
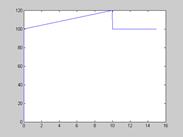
Рис. 29. Зависимость момента от времени 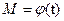 для параболической зависимости скорости СЭП
для параболической зависимости скорости СЭП
На рис. 30  33 представлены зависимости
33 представлены зависимости 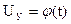 для указанных выше заданных зависимостей скоростей СЭП.
для указанных выше заданных зависимостей скоростей СЭП.
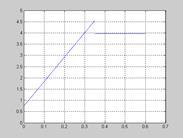
Рис. 30. Зависимость напряжения задания СЭП от времени  для линейной зависимости скорости СЭП
для линейной зависимости скорости СЭП
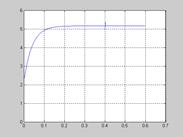
Рис. 31. Зависимость напряжения задания СЭП от времени  для экспоненциальной зависимости скорости СЭП
для экспоненциальной зависимости скорости СЭП
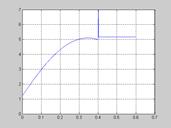
Рис. 32. Зависимость напряжения задания СЭП от времени 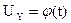 для синусоидальной зависимости скорости СЭП
для синусоидальной зависимости скорости СЭП
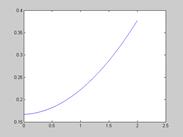
Рис. 33. Зависимость напряжения задания СЭП от времени 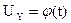 для параболической зависимости скорости СЭП
для параболической зависимости скорости СЭП
Заданные графики скоростей СЭП (рис. 22 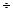 25) представлены в виде аналитических зависимостей. Линейный график скорости от времени
25) представлены в виде аналитических зависимостей. Линейный график скорости от времени  представлен зависимостью
представлен зависимостью 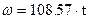 , экспоненциальный график представлен зависимостью
, экспоненциальный график представлен зависимостью 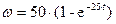 , синусоидальный график представлен зависимостью
, синусоидальный график представлен зависимостью 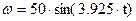 , параболический график представлен зависимостью
, параболический график представлен зависимостью 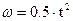 . Это позволяет некоторые операции синтеза выполнить в аналитической форме.
. Это позволяет некоторые операции синтеза выполнить в аналитической форме.
Выражение для момента двигателя определяется по формуле 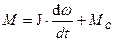 . Дифференцирование зависимости скорости для линейно – нарастающего участка графика
. Дифференцирование зависимости скорости для линейно – нарастающего участка графика  приводит к следующей зависимости
приводит к следующей зависимости 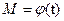 .
. 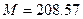
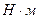 = const, а для участка постоянной скорости
= const, а для участка постоянной скорости 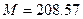
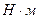 , что соответствует результатам численного синтеза (рис. 26). Для экспоненциального графика
, что соответствует результатам численного синтеза (рис. 26). Для экспоненциального графика  получим
получим 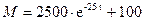 , что совпадает с результатами численного синтеза (рис. 27). Синусоидальная зависимость
, что совпадает с результатами численного синтеза (рис. 27). Синусоидальная зависимость  позволяет получить следующее выражение для момента двигателя, которое хорошо согласуется с синтезом (рис. 28).
позволяет получить следующее выражение для момента двигателя, которое хорошо согласуется с синтезом (рис. 28). 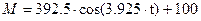 . Для параболической зависимости скорости СЭП полученное выражение для момента двигателя
. Для параболической зависимости скорости СЭП полученное выражение для момента двигателя 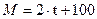 также совпадает с результатами численного синтеза (рис. 29).
также совпадает с результатами численного синтеза (рис. 29).
Для напряжения цепи якоря может быть получено аналитическое уравнение 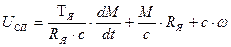 , что позволяет подставить в него выражения
, что позволяет подставить в него выражения 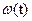 и
и 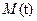 для заданных графиков скоростей СЭП.
для заданных графиков скоростей СЭП.
Дата добавления: 2020-10-25; просмотров: 787;











