Подготовка уравнений для построения модели АД с кз ротором при частотном управлении в форме структурной схемы

Представим комплексные векторы в выражении (143) в алгебраической форме (в виде вещественных и мнимых составляющих) и определим проекции тока ротора на вещественную и мнимую оси системы координат « 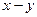», вращающейся с угловой скоростью, равной .

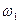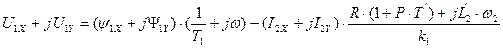. (144)

Определим 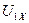и , и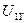спользуя уравнения фазовых преобразований (62)-(65).

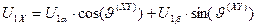. (145)

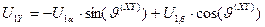. (146)

Допустим, что 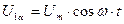. (147)

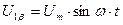. (148)

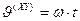. (149)

Подставим выражения (147)-(149) в уравнения (145) и (146). Получим

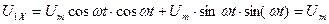. (150)

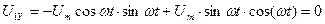. (151)

Если проекции обобщенного вектора в неподвижной системе координат « 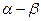» изменяются во времени по синусоидальному закону с частотой 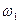, то проекции этого же обобщенного вектора в системе координат « 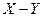», вращающейся с угловой скоростью 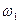, являются постоянными величинами.

Преобразуем уравнение (144) и приравняем действительные и мнимые части в правой и левой частях выражений (144) и получим два уравнения для модели АД с кз ротором при частотном управлении в форме структурной схемы.

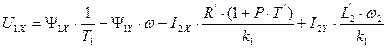. (152)

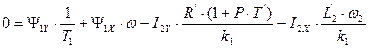. (153)

Из уравнений (152) и (153) определим 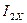и .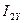

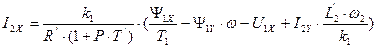. (154)

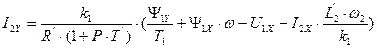. (155)

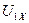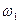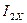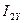Выражения позволяют построить структурную схему преобразования напряжения и частоты статора в фазные токи ротора и обобщенного АД при известных проекциях вектора потокосцепления статора 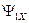, 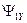и частоты вращения ротора 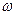. Но потокосцепление статора можно выразить через ток ротора с помощью выражения (141), преобразуя которое получим

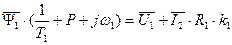. (156)

Представим комплексные векторы в выражении (156) в алгебраической форме в виде вещественных и мнимых составляющих и преобразуем уравнение (157), приравнивая действительные и мнимые части в правой и левой частях выражения (157). Получим с учетом того, что ,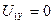

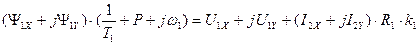. (157)

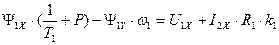. (158)

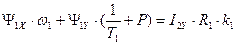. (159)

Из уравнения (158) определим 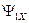, а решая уравнение (159), найдем .

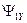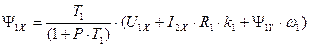. (160)

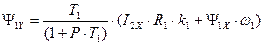. (161)

Тогда, с учетом основного уравнения привода получим структурную схему АД. .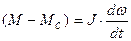

Структура АД нелинейная и имеет четыре перекрестные связи.

Упростить структуру АД для получения передаточных функций по каналам управления напряжением и частотой крайне затруднительно, но не представляет большого труда построить эту модель в системе Matlab/Simulink и получить требуемые характеристики привода при различных законах управления, связывающих какой-либо функцией 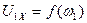входы управления частотой и напряжением статора.